Integers Class 6 Notes Maths Chapter 1
Representing Movements
- Positive Numbers: When we talk about moving to the right of zero, we use positive numbers.
For example: +7 : This means moving 7 steps to the right from zero on a number line or position strip.
If you walk 7 steps to the right from your starting point, your position is represented as +7. - Negative Numbers: When we talk about moving to the left of zero, we use negative numbers.
For example:–6: This means moving 6 steps to the left from zero on a number line or position strip. If you walk 6 steps to the left from your starting point, your position is represented as –6.
Successor and Predecessor
- The successor is the number that comes immediately after a given number. If we move 1 to the right then it gives the successor of that number
- The predecessor is the number that comes immediately before a given number. If we move 1 to the left then it gives the predecessor of that number.
| Number | Predecessor | Successor |
| 2 | 1 | 3 |
| -8 | -9 | -7 |
| -3 | -4 | -2 |
| 4 | 3 | 5 |
Integers
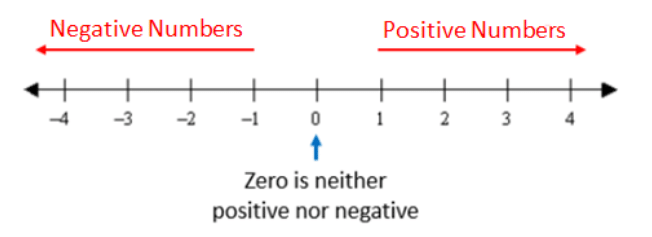
- The collection of whole numbers and negative numbers together are called the Integers.
- All the positive numbers are positive integers and all the negative numbers are negative integers.
- Zero is neither a positive nor a negative integer.
Representation of Integers on Number Line
Step 1: First, we have to draw a line and mark a point zero on it.
Step 2: Then mark all the positive integers on the right side with the same distance as 1, 2, 3… and the entire negative numbers on the left side as -1,-2,-3…
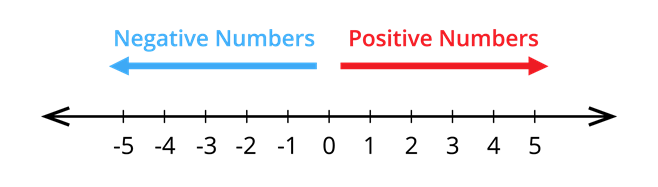
Step 3: Now let us say we want to mark -7, for this we have to move 7 points to the left of zero.
Ordering of Integers
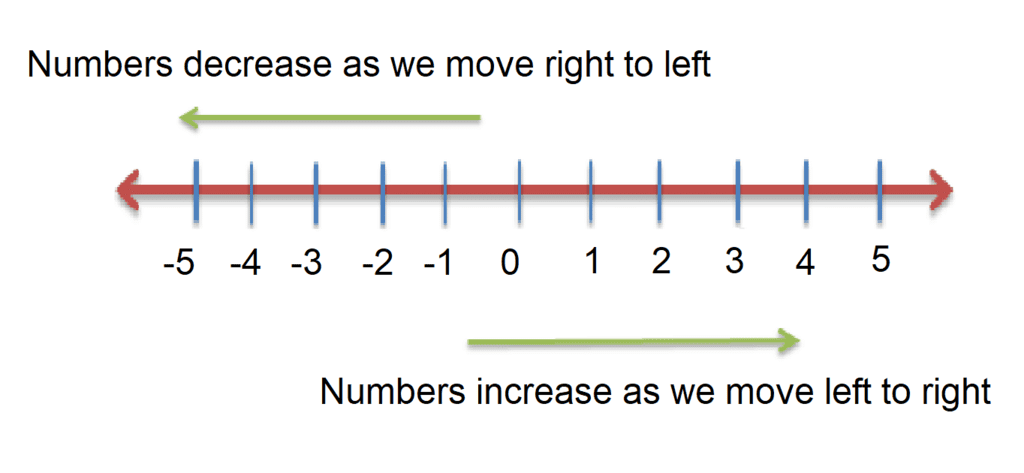
- Increasing Order: Positive numbers increase as you move to the right on the number line.
Example: 3 < 7 (3 is to the left of 7 on the number line) - Decreasing Order: Negative numbers decrease as you move to the left on the number line.
Example: –7 < –3 (–7 is to the left of –3 on the number line) - Positive vs. Negative: Any positive number is greater than any negative number.
Example: 5 > –2 (5 is to the right of –2 on the number line)
Example: Order from Smallest to Largest: 7, –1, –4, 3, 0, -8
- Negative Numbers: –8 < –4 < –1
- Zero: 0 is greater than all negative numbers but less than positive numbers.
- Positive Numbers: 3 < 7
- Order from Smallest to Largest: –8, –4, –1, 0, 3, 7
Addition of Integers
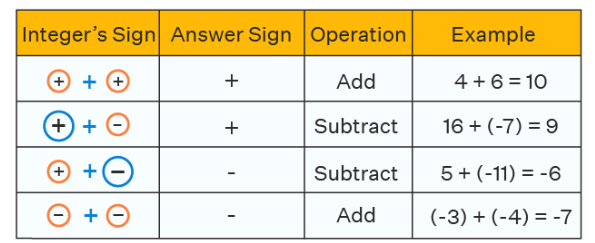
1. Addition of Two Positive Integers
If you have to add two positive integers then simply add them as natural numbers.
(+6) + (+7) = 6 + 7 = 13
2. Addition of Two Negative Integers
If we have to add two negative integers then simply add them as natural numbers and then put a negative sign on the answer.
(-6) + (-7) = - (6+7) = -13
3. Addition of One Negative and One Positive Integer
If we have to add one negative and one positive integer then simply subtract the numbers and put the sign of the bigger integer. We will decide the bigger integer ignoring the sign of the integers.
- (-6) + (7) = 1 (bigger integer 7 is positive integer)
- (6) + (-7) = -1(bigger integer 7 is negative integer)
Addition of Integers on a Number Line
1. Addition of Two Positive Integers
Example: Add 3 and 4 on the number line.
Sol: To add 3 and 4, first, we move 3 steps to the right of zero then again move 4 steps to the right from point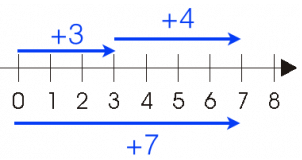
As we reached to the point 7, hence (+3) + (+4) = +7
This shows that the sum of two positive integers is always positive.
2. Addition of Two Negative Integers
Example: Add (-2) and (-5) using a number line.
Sol: To add (-2) and (-5), first we move 2 steps to the left of zero then again move 5 steps to the left of (-2).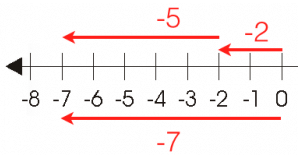 As we reached to the point (-7), hence (-2) + (-5) = -7.
As we reached to the point (-7), hence (-2) + (-5) = -7.
This shows that the sum of two negative integers is always negative.
3. Addition of One Negative and One Positive Integer
(a) If a positive integer is greater than the negative integer
To add (+6) and (-2), first we have to move 6 steps to the right from zero then move 2 steps to the left of point 6.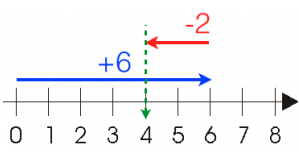
As we reached to the point 4, hence (+6) + (-2) = +4
(b) If a negative integer is greater than the positive integer
To add (-5) and (+4), first we have to move 5 steps to the left of zero then move 4 steps to the right from point (-5).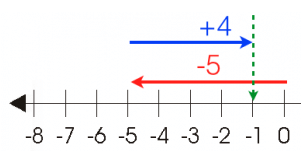
As we reached to the point -1, hence (-5) + (+4) = (-1)
4. Additive Inverse
If we add numbers like (-7) and 7 then we get the result as zero. So these are called the Additive inverse of each other.
For Example:
What is the additive inverse of 4 ?
Sol: The additive inverse of 4 is (-4).
Subtraction of Integers on Number Line
If we subtract an integer from another integer then we simply add the additive inverse of that integer.
(-3) – (-2) = (-3) + 2 = -1
(-3) – (+2) = (-3) + (-2) = -5
1. Subtraction of Two Positive Integers
Example: Subtract 2 from 5.
Solution: To subtract 2 from 5, first, we move 5 steps to the right from zero then move 2 steps back to the left.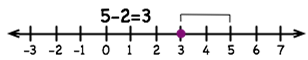
As we reached to 3 hence, 5 – (+2) = 5 – 2 = 3
2. Subtraction of Two Negative Integers
Example: Subtract (-12) from (-8).
Solution: To subtract (-12) from (-8), first, we have to move 8 steps to the left of zero then move 12 steps to the right of (-8).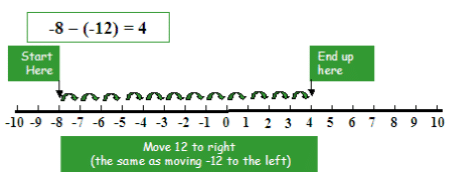
As we reached to 4, hence (-8) – (-12) = (-8) + (12) = 4
3. Subtraction of One Negative and One Positive Integer
(a) To subtract a positive integer from any other integer.
Example: Subtract 3 from (-4)
Solution: To subtract (-4) from (3), first, we have to move 4 steps to the left of zero then move 3 steps more to the left.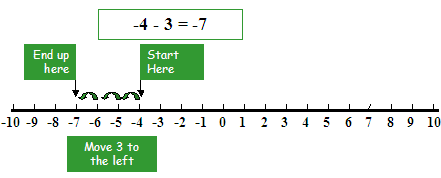
As we reached to (-7), hence (-4) – (+3) = (-4) + (-3) = -7.
(b) To subtract a negative integer from any other integer
Example: Subtract (-3) from (4)
Solution: To subtract (-3) from (4), first, we have to move 4 steps to the right of zero then move 3 steps more to the right.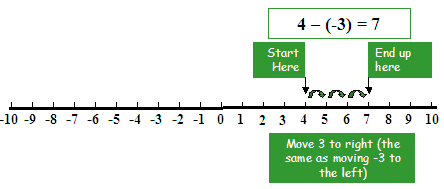 As we reached to (7), hence (4) – (-3) = (4) + (+3) = +7
As we reached to (7), hence (4) – (-3) = (4) + (+3) = +7
|
42 videos|59 docs|22 tests
|
FAQs on Integers Class 6 Notes Maths Chapter 1
| 1. How are integers represented on a number line? |  |
| 2. How do you determine the order of integers? |  |
| 3. How do you add integers together? |  |
| 4. How do you subtract integers on a number line? |  |
| 5. How can you represent the successor and predecessor of an integer? |  |






















