Algebra Class 6 Notes Maths Chapter 11
| Table of contents |

|
| Algebra |

|
| Variable |

|
| Use of Variables in Common Rules (Geometry) |

|
| Expressions |

|
| Equation |

|
| Solution of an Equation |

|
Algebra
Algebra is a part of mathematics in which the letter and symbols are used to represent numbers in equations. It helps us to study about unknown quantities.
Matchstick Patterns
- No. of matchsticks used to make 1st square = 4
- No. of matchsticks used to make 2nd square = 7
- No. of matchsticks used to make 3rd square = 10
- So, the pattern that we observe here is 3n + 1
- With this pattern, we can easily find the number of matchsticks required in any number of squares.
Variable
Variable refers to the unknown quantities that can change or vary and are represented using the lowercase letter of the English alphabets.
For Example:
The rule that we used in the matchstick pattern 3n + 1
Here the value of n is unknown and it can vary from time to time.
Example : Karan wanted to buy story books from a bookstall. She wanted to buy 3 books for herself, 2 for her brother and 4 for 2 of her friends. Each book cost Rs.15.how much money she should pay to the shopkeeper?
Sol:
Cost of 1 book = Rs.15
We need to find the cost of 9 books.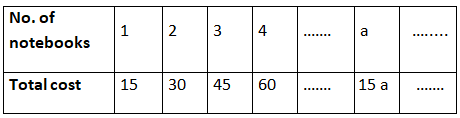
In the current situation, a (it’s a variable) stands for 9
Therefore,
Cost of 9 books = 15 × 9
= 135
Therefore Karan needs to pay Rs.135 to the shopkeeper of the bookstall.
The variable and constant not only multiply with each other but also can be added or subtracted, based on the situation.
Use of Variables in Common Rules (Geometry)
1. Perimeter of Square
The perimeter of a square = Sum of all sides
= 4 × side
= 4s
Thus, p = 4s
Here s is variable, so the perimeter changes as the value of side change.
2. Perimeter of Rectangle
Perimeter of rectangle = 2(length + breadth)
= 2 (l + b) or 2l + 2b
Thus, p + 2 × (l + b) or 2l + 2b
Where, l and b are variable and the value of perimeter changes with the change in l and b.

Use of Variables in Common Rules (Arithmetic)
1. Commutativity of Addition
a + b = b + a
Here, a and b are different variables.
Example:
a = 16 and b = 20
According to commutative property
16 + 20 = 20 + 16
36 = 36
2. Commutativity of Multiplication
a × b = b × a
Here, a and b are different variables.
Example:
18 ×12 = 216,12 ×18 = 216
Thus, 18 × 12 = 12 × 18
3. Distributivity of Numbers
a × (b + c) = a × b + a × c
Here, a, b and c are different variables.
4. Associativity of Addition
This property states that the result of the numbers added will remain same regardless of their grouping
(a + b) + c = a + (b + c)
Example:
(4 + 2) + 7 = 4 + (2 + 7)
6 + 7 = 4 + 9
13 = 13
Expressions
Arithmetic expressions may use numbers and all operations like addition, subtraction, multiplication and division
Example: Find 3x – 12 if x = 6
Sol: (3 × 6) – 12
= 18 – 12
= 5
Thus,
3x – 12 = 5
Formation of Expressions
| Statement | Expression |
| y subtracted from 12 | 12 - y |
| x multiplied by 6 | 6x |
| t Multiplied by 4, and then subtract 5 from the product. | 4t - 5 |
Equation
If we use the equal sign between two expressions then they form an equation.
An equation satisfies only for a particular value of the variable.
The equal sign says that the LHS is equal to the RHS and the value of a variable which makes them equal is the only solution of that equation.
Example: 3 + 2x = 13
5m – 7 = 3
p/6 = 18
Note:
If there is the greater then or less than sign instead of the equal sign then that statement is not an equation.
Some examples which are not an equation
23 + 6x > 8
6f – 3 < 24
Solution of an Equation
The value of the variable which satisfies the equation is the solution to that equation. To check whether the particular value is the solution or not, we have to check that the LHS must be equal to the RHS with that value of the variable.
Trial and Error Method
To find the solution of the equation, we use the trial and error method.
Example: Find the value of x in the equation 25 – x = 15.
Sol: Here we have to check for some values which we feel can be the solution by putting the value of the variable x and check for LHS = RHS.
Let’s take x = 5
25 – 5 = 15
20 ≠ 15
So x = 5 is not the solution of that equation.
Let’s take x = 10
25 – 10 = 15
15 = 15
LHS = RHS
Hence, x = 10 is the solution of that equation.
|
141 videos|210 docs|58 tests
|
FAQs on Algebra Class 6 Notes Maths Chapter 11
| 1. What is a variable in algebra? |  |
| 2. How are variables used in geometric formulas? |  |
| 3. What is the difference between an expression and an equation? |  |
| 4. How do you solve a simple equation? |  |
| 5. What are some common rules for manipulating algebraic expressions? |  |





















