The Triangle and Its Properties Class 7 Notes Maths Chapter 6
Triangle is a closed curve made up of three line segments. It has three vertices, sides and angles.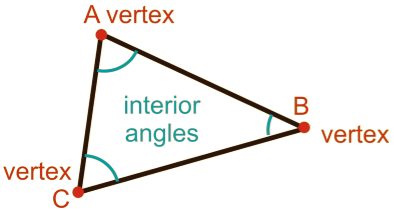 Here, in ∆ABC,
Here, in ∆ABC,
- AB, BC and CA are the three sides.
- A, B and C are three vertices.
- ∠A, ∠B and ∠C are the three angles.
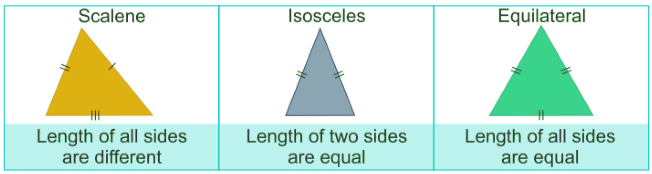
Types of Triangle on the basis of sides
Types of Triangle on the basis of angles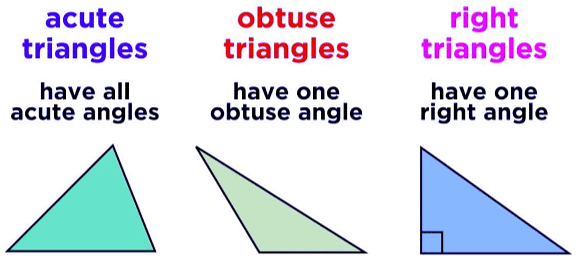
Medians of a Triangle
Median is the line segment which made by joining any vertex of the triangle with the midpoint of its opposite side. Median divides the side into two equal parts.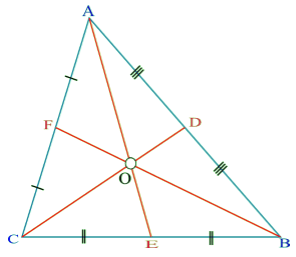 Every triangle has three medians like AE, CD and BF in the above triangle.
Every triangle has three medians like AE, CD and BF in the above triangle.
The point where all the three medians intersect each other is called Centroid.
Altitudes of a Triangle
Altitude is the line segment made by joining the vertex and the perpendicular to the opposite side. Altitude is the height if we take the opposite side as the base.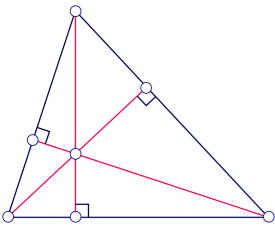
- The altitude form angle of 90°.
- There are three altitudes possible in a triangle.
- The point of intersection of all the three altitudes is called Orthocenter.
The Exterior Angle of a Triangle
If we extend any side of the triangle then we get an exterior angle.
- An exterior angle must form a linear pair with one of the interior angles of the triangle.
- There are only two exterior angles possible at each of the vertices.
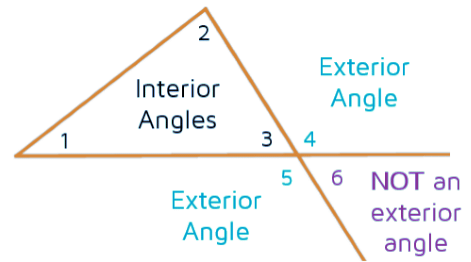
Here ∠4 and ∠5 are the exterior angles of the vertex but ∠6 is not the exterior angle as it is not adjacent to any of the interior angles of the triangle.
Exterior Angle Property of the Triangle
An Exterior angle of a triangle will always be equal to the sum of the two opposite interior angles of the triangle.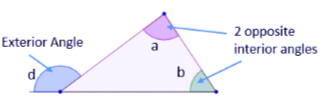
Here, ∠d = ∠a + ∠b
This is called the Exterior angle property of a triangle.
Example: Find the value of “x”.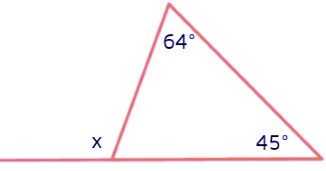 Sol: x is the exterior angle of the triangle and the two given angles are the opposite interior angles.
Sol: x is the exterior angle of the triangle and the two given angles are the opposite interior angles.
Hence,
x = 64°+ 45°
x = 109°
Angle Sum Property of a Triangle
This property says that the sum of all the interior angles of a triangle is 180°.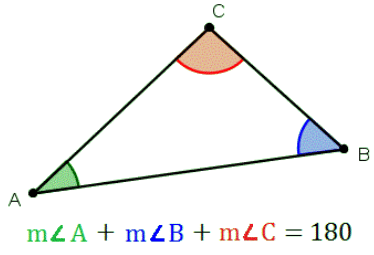 Example: Find the value of x and y in the given triangle.
Example: Find the value of x and y in the given triangle.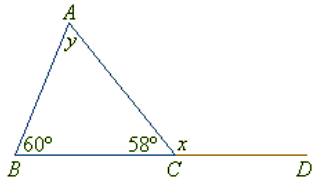
Sol: x + 58° = 180° (linear pair)
x = 180° - 58°
x = 122°
We can find the value of y by two properties-
1. Angle sum property
60° + 58° + y = 180°
y = 180°- (60° + 58)
y = 62°
2. Exterior angle property
x = 60°+ y
122° = 60° + y
y = 122° - 60°
y = 62°
Two Special Triangles
1. Equilateral Triangle
It is a triangle in which all the three sides and angles are equal.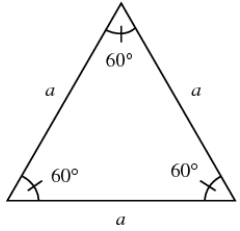
2. Isosceles Triangle
It is a triangle in which two sides are equal and the base angles opposite to the equal sides are also equal.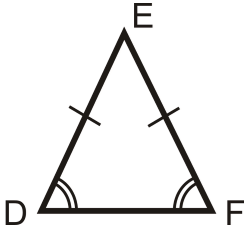
Sum of the length of the two sides of a triangle
Sum of the length of the two sides of a triangle will always be greater than the third side, whether it is an equilateral, isosceles or scalene triangle.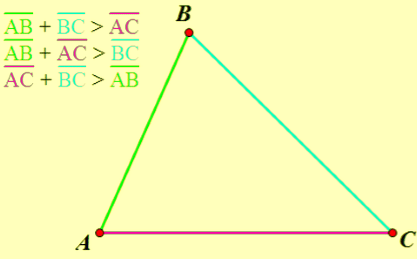
Example: Check whether it is possible to make a triangle using these measurements or not?
1. 3 cm, 4 cm, 7 cm
We have to check whether the sum of two sides is greater than the third side or not.
4 + 7 = 11
3 + 7 = 10
3 + 4 =7
Here the sum of the two sides is equal to the third side so the triangle is not possible with these measurements.
2. 2 cm, 5 cm, 6 cm
2 + 5 = 7
6 + 5 = 11
6 + 2 = 8
Here the sum of the two sides is greater than the third side so the triangle could be made with these measurements.
Right Angled Triangle
A right-angled triangle is a triangle which has one of its angles as 90° and the side opposite to that angle is the largest leg of the triangle which is known as Hypotenuse .the other two sides are called Legs.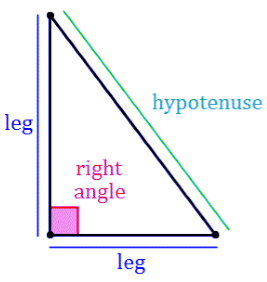
Pythagoras theorem
In a right angle triangle,
(Hypotenuse)2 = (base)2 + (height)2
The reverse of Pythagoras theorem is also applicable, i.e. if the Pythagoras property holds in a triangle then it must be a right-angled triangle.
Example
Find the value of x in the given triangle if the hypotenuse is 5 cm and height is 4 cm.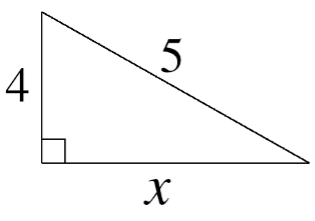
Sol: Given:
Hypotenuse = 5 cm
Height = 4 cm
Base = x cm
(Hypotenuse)2 = (base)2 + (height)2
52 = x2 + 42
x2 = 52 - 42
x2 = 25 – 16
x = 9
x = 3 cm
|
77 videos|386 docs|39 tests
|
FAQs on The Triangle and Its Properties Class 7 Notes Maths Chapter 6
| 1. What is the median of a triangle and how is it constructed? |  |
| 2. What is the importance of the altitude in a triangle? |  |
| 3. What is the Exterior Angle Property of a triangle? |  |
| 4. How does the Angle Sum Property apply to triangles? |  |
| 5. What is the significance of the Pythagorean theorem in right-angled triangles? |  |

















