Perimeter and Area Class 7 Notes Maths Chapter 9
| Table of contents |

|
| Area |

|
| Area and Perimeter of Rectangle |

|
| Triangles as Parts of Rectangles |

|
| Congruent Parts of Rectangles |

|
| Parallelogram |

|
| Area of Triangle |

|
| Circles |

|
| Area of Circle |

|
| Conversion of Units |

|
It refers to the length of the outline of the enclosed figure.
Area
It refers to the surface of the enclosed figure.
Area and Perimeter of Square
Square is a quadrilateral, with four equal sides.
Area = Side × Side
Perimeter = 4 × Side
Example: Find the area and perimeter of a square-shaped cardboard whose length is 5 cm.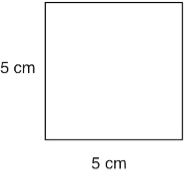
Sol: Area of square = (side)2
= (5)2
= 25 cm2
Perimeter of square = 4 × side
= 4 × 5
= 20 cm
Area and Perimeter of Rectangle
The rectangle is a quadrilateral, with equal opposite sides.
Area = Length × Breadth
Perimeter = 2(Length + Breadth)
Example: What is the length of a rectangular field if its width is 20 ft and Area is 500 ft2?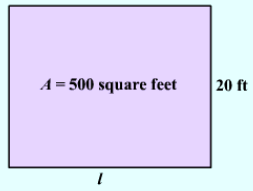 Sol: Area of rectangular field = length × width
Sol: Area of rectangular field = length × width
500 = l × 20
l = 500/20
l = 25 ft
Triangles as Parts of Rectangles
If we draw a diagonal of a rectangle then we get two equal sizes of triangles. So the area of these triangles will be half of the area of a rectangle. The area of each triangle = 1/2 (Area of the rectangle)
The area of each triangle = 1/2 (Area of the rectangle)
Likewise, if we draw two diagonals of a square then we get four equal sizes of triangles .so the area of each triangle will be one-fourth of the area of the square.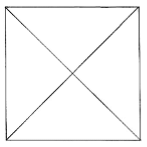 The area of each triangle = 1/4 (Area of the square)
The area of each triangle = 1/4 (Area of the square)
Example: What will be the area of each triangle if we draw two diagonals of a square with side 7 cm?
Sol: Area of square = 7 × 7
= 49 cm2
The area of each triangle = 1/4 (Area of the square)
= 1/4 × 49
= 12.25 cm2
Congruent Parts of Rectangles
Two parts of a rectangle are congruent to each other if the area of the first part is equal to the area of the second part.
Example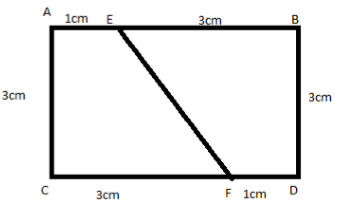 The area of each congruent part = 1/2 (Area of the rectangle)
The area of each congruent part = 1/2 (Area of the rectangle)
= 1/2 (l × b) cm2
=1/2 (4 × 3) cm2
= 1/2 (12) cm2
= 6 cm2
Parallelogram
It is a simple quadrilateral with two pairs of parallel sides. Also denoted as ∥ gm
Area of parallelogram = base × height
Or b × h (bh)
We can take any of the sides as the base of the parallelogram. And the perpendicular drawn on that side from the opposite vertex is the height of the parallelogram.
Example: Find the area of the figure given below: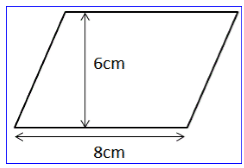
Sol: Base of ∥ gm = 8 cm
Height of ∥ gm = 6 cm
Area of ∥ gm = b × h
= 8 × 6
= 48 cm
Area of Triangle
Triangle is a three-sided closed polygon. If we join two congruent triangles together then we get a parallelogram. So the area of the triangle will be half of the area of the parallelogram.
Area of Triangle = 1/2 (Area of ∥ gm)
= 1/2 (base × height)
Example: Find the area of the figure given below: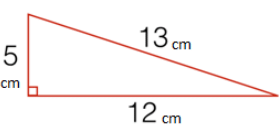
Sol: Area of triangle = 1/2 (base × height)
= 1/2 (12 × 5)
= 1/2 × 60
= 30 cm2
 |
Download the notes
Short Notes: Perimeter and Area
|
Download as PDF |
Circles
It is a round, closed shape.
The circumference of a Circle
The circumference of a circle refers to the distance around the circle.
- Radius: A straight line from the Circumference till the centre of the circle.
- Diameter: It refers to the line from one point of the Circumference to the other point of the Circumference.
- π (pi): It refers to the ratio of a circle's circumference to its diameter.
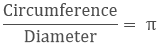
Circumference(c) = π × diameter
C = πd
= π × 2r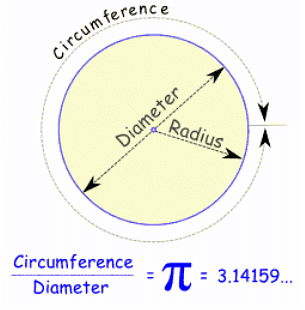 d = 2r
d = 2r
Example: What is the circumference of a circle of diameter 12 cm (Take π = 3.14)?
Sol: C = πd
C = 3.14 × 12
= 37.68 cm
Area of Circle
Area of the circle = (Half of the circumference) × radius
= πr2
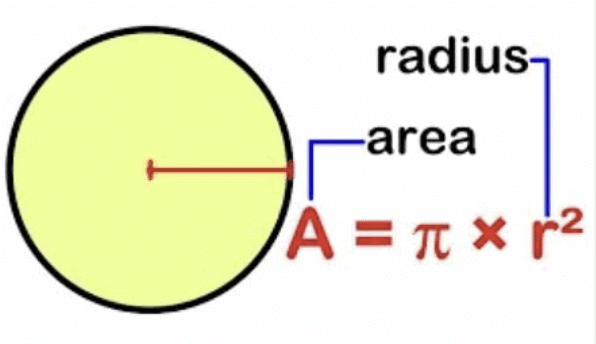 Example: Find the area of a circle of radius 23 cm (use π = 3.14).
Example: Find the area of a circle of radius 23 cm (use π = 3.14).
Sol: R = 23 cm
π = 3.14
Area of circle = 3.14 × 232
= 1,661 cm2
Conversion of Units
Sometimes we need to convert the unit of the given measurements to make it similar to the other given units.

Conversion of Units
Unit | Conversion |
1 cm | 10 mm |
1 m | 100 cm |
1 km | 1000 m |
1 hectare(ha) | 100 × 100 m |
Unit | Conversion |
1 cm2 | 100 mm2 |
1 m2 | 10000 cm2 |
1 km2 | 1000000 m2 (1e + 6) |
1 ha | 10000 m2 |
Example 1: Convert 70 cm2 in mm2
Sol:
1 cm = 10 mm
1 cm2 = 10 × 10
1 cm2 = 100 mm2
70 cm2 = 700 mm2
Example: 2 Convert 3.5 ha in m2
Sol: 1 ha = 10000 m2
3.5 ha = 10000 × 3.5
ha = 35000 m2
Applications
We can use these concepts of area and perimeter of plane figures in our day to day life.
- If we have a rectangular field and want to calculate that how long will be the length of the fence required to cover that field, then we will use the perimeter.
- If a child has to decorate a circular card with the lace then he can calculate the length of the lace required by calculating the circumference of the card, etc.
Example: A rectangular park is 35 m long and 20 m wide. A path 1.5 m wide is constructed outside the park. Find the area of the path.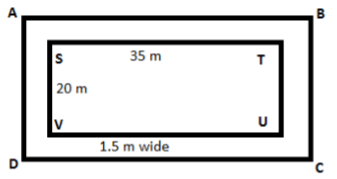 Sol: Area of rectangle ABCD – Area of rectangle STUV
Sol: Area of rectangle ABCD – Area of rectangle STUV
AB = 35 + 2.5 + 2.5
= 40 m
AD = 20 + 2.5 + 2.5
= 25 m
Area of ABCD = 40 × 25
= 1000 m2
Area of STUV = 35 × 20
= 700 m2
Area of path = Area of rectangle ABCD – Area of rectangle STUV
= 1000 – 700
= 300 m2
|
77 videos|388 docs|39 tests
|
FAQs on Perimeter and Area Class 7 Notes Maths Chapter 9
| 1. What is the formula for the area of a rectangle? |  |
| 2. How do you calculate the perimeter of a rectangle? |  |
| 3. What is the area of a triangle, and how is it calculated? |  |
| 4. How do you find the area of a circle? |  |
| 5. What is the relationship between the area of different shapes, like triangles and rectangles? |  |



















