Calendar: Shortcut & Tricks | Quantitative Techniques for CLAT PDF Download
| Table of contents |

|
| Basic Structure of a Calendar |

|
| Concept of an Odd Day |

|
| Evaluation of leap year |

|
| Decoded day of the week |

|
| Zeller’s Formula |

|
Basic Structure of a Calendar
- Ordinary year: Any year which 365 days is called an ordinary year. Ex: 1879, 2009, 2019, etc.
- Leap year: Any year which has 366 days is called a leap year. Ex: 2012, 2016 2020 etc.
- The division of the number 365 by 7 gives the quotient 52 and remainder 1 which indicates that an ordinary year has 52 weeks and one extra day. This extra day is referred to as an “odd day” throughout the calendar topics.
- A leap year has 366 days, the division of the number 366 by 7 gives the quotient 52 and remainder 2. This indicates that a leap year has 52 weeks and 2 extra days. These two extra days are also referred to as “odd days”.
An ordinary year has one odd day, whereas a leap year has two odd days.
Concept of an Odd Day
January has 31 days irrespective of whether it’s an ordinary year or leap year. The division of the number 31 by 7 provides the remainder 3 hence the January has 3 odd days. On generalizing, any month which has 31 days has 3 odd days and any month which has 30 days has 2 odd days.
The only exception happens is in the case of February. The February month of an ordinary year has 28 days, division of 28 by 7 provides zero as remainder. Hence the number of odd days in February of an ordinary year will have 0 odd days and that of leap year will have 1 odd day as February in a leap year has 29 days.
The below table depicts the number of odd days in different months of a calendar year:
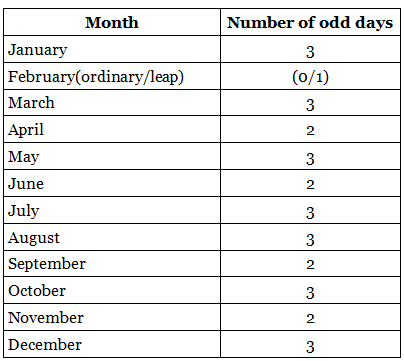
Evaluation of leap year
The Earth actually completes 1 orbit around the Sun in more than 365 days, i.e in 365 Days 5 Hours 48 minutes and 45 seconds or takes approximately 6 hours more. A leap year occurs every 4 years to adjust for the 1/4th day, 6 x 4= 24 hours, so every 4th year has 366 days (or 2 odd days). And as far as the few odd minutes of the orbit time are concerned, well every 100 years starting 1 AD, the year is declared to be a non–leap year, but every 4th century is a leap year. So any year divisible by 400 will be a leap year e.g.: 1200, 1600 and 2000. The years 1800, 1900 will be non leap years.
Decoded day of the week
The week always begins with Monday and hence the Saturday and Sunday are referred to as weekends. In order to make the calculation easier and reduce its time during the exams.
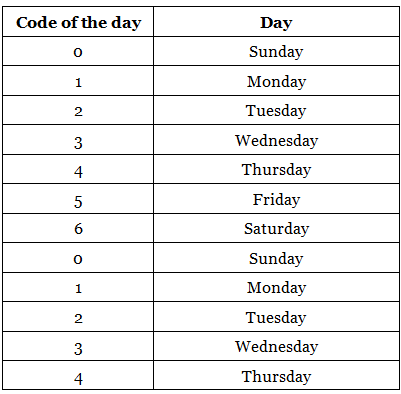
The days of the week are coded as follows:
The week always begins with Monday and hence counting that as 1, 5 stands for Friday.
Extension of the logic
Similarly, one can find the last day of the other century years by extending the same logic.
If 100 years had 5 odd days, then logically 200 years should have 10 odd days. Since 10 is greater than 7, the division of 10 by 7 gives the remainder 3. Hence, the 200 years had 3 odd days, which means the last day of the year 200 was Wednesday.
Number of odd days in 200 years = (5 x 2) = 10 = (7 3) = 3 odd days.
If 100 years had 5 odd days and 200 years 10 odd days logically 300 years should have 15 odd days. The division of 15 by 7 indicates it has 1 odd day from the remainder which indicates it is Monday. Hence, the last day of the year 300 was Monday.
Number of odd days in 300 years = (5 x 3) = 15 = (14 1) = 1 odd day.
Logically, 400 years should have 20 odd days since 400th year is a leap year as it is divisible by 400. This year will have 20 1 = 21 odd days, which when divided by 7 gives the zero (0) as remainder. Hence, 400 years had 0 odd days and that was Sunday.
The logical approach for the next few years is shown in the table given below:
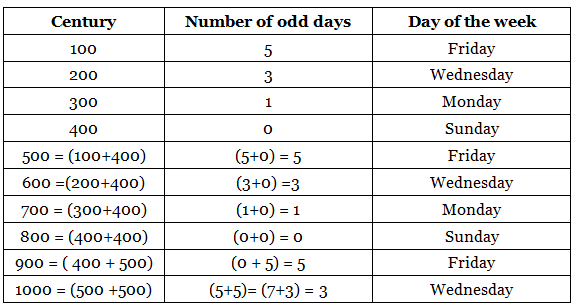
Observations from the table:
- The cycle of a number of days repeats after every four centuries and also hence the days at which it ends. The order will always be Friday, Wednesday Monday, and Sunday.
- A century will always end on either Friday, Wednesday, Monday, or Sunday (Decoded values of these days are 5, 3, 1, and 0 respectively).
- A century will never end on Tuesday, Thursday, and Saturday (Decoded values of these days are 2, 4, and 6 respectively).
Zeller’s Formula
Along with these tricks, we can also use Zeller’s Formula. i.e.
d=k [(13m-1)/5] D [D/4] [C/4]-2C mod 7
- Here d is the day of the week where we will see the day code in the above-given table.
- K is the day of the month.
- D is the last two digits of the year
- C is the century, will take as first two digits of the year.
- The [ ] brackets reveal the high integer function.
- Which is the largest integer less than and equal to the number inside.
- M= month, but we will start the year with the month March=1, so January and February will the 11th and 12th month of the last year.
Example
What was the day on 7- December-1941?
(As I know it was Sunday, but here I will do through this formula)
d=7 [(13*10-1)/5] 41 [41/4] [19/4]-2*19 mod 7
=7 [25.8] 41 [10.25] [4.75]-38 mod 7
=7 25 41 10 4-38 mod 7
=49 mod 7
=0 mode 7
So here we got the 0, which reveals I table code as Sunday, so the answer is Sunday. This formula works only for the Gregorian calendar.
Example:
Question: What day of the week was 15th August 1947?
Sol: The date of August 15, 1947, can be divided as follows for easy calculation:
1600 years + 300 years+ 46 years (1901 to 1946) + Jan 1st to august 15th (of 1947)
Note:- Do not write 47 years in the third section, it would indicate 47th year in that century is over.
1600 years + 300 years+ 46 years (1901 to 1946) + Jan 1st to august 15th (of 1947)
Now let’s find out the total number of odd days in each section:
Section 1:
1600 is a multiple of 400 years. 400 years have 0 odd days hence 1600 years should have 0 odd days.
Section 2:
The second section 30 years will have 1 odd day. Kindly refer to the “evaluation of odd days in a century” topic for clarification.
Section 3:
This section has 46 years from 1901 to 1946, we know that an ordinary year has one odd day and a leap year has 2 odd days.
Let’s first calculate the total number of leap years from 1901 to 1946.
Division of 46 by 4 gives the quotient as 11, which indicates that from 1901 to 1946 we have 11 leap years. If there are 11 leap years among 46 years then the remaining 35 years should be ordinary years. Hence, 35 ordinary years will have 35 odd days and 11 leap years will have 11*2 = 22 years.
The total number of odd days in 46 years will be 35+22 = 57 odd days. The division of 57 by 7 given the remainder as 1.This indicates from 1901 to 1946 there is only one odd day.
Section 4:
It has months from January to August 15th. We have already calculated the total number of odd days in each month in the odd day’s section.
Since 1947 is not a leap year February had zero odd days.
The total number of odd days is 31 which when divided by 7 gives the remainder 3. Hence, the total number of odd days in the year 1947 from January 1st to August 15th is 3.
Adding the total number of odd days of each section:
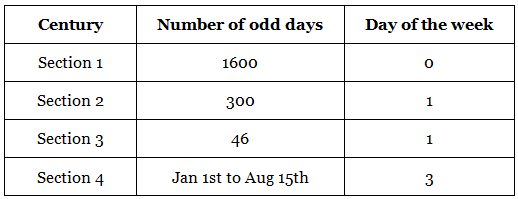
|
49 videos|155 docs|73 tests
|















