Time and Work: Shortcut & Tricks | Quantitative Techniques for CLAT PDF Download
Time and Work is the widely asked topic in every exam for the past many years. If you are preparing for any government exam, then your concept of this topic should be very clear. Let’s revise all the concepts of Time and work from this article and learn time and work tricks to save time in exams through the following time and work-study notes.
Concept of Time and Work
Time: Time is the duration during which any activity or work happens or continues.
Work: Work is a task or set of activities to achieve a certain result.
We can define happening of work as:
- If a person A completes a work in X days, then the amount of work completed by him in 1 day will be =1/X
- Similarly, if a person B completes work in Y days, then the amount of work completed by him in 1 day will be = 1/Y
- From the above two points, we can say that in one day A and B together can complete
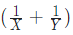 amount of work. Thus, together A and B can complete the work in
amount of work. Thus, together A and B can complete the work in 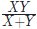 days.
days.
Here, we have assumed total work as 1 unit. Similarly, we can assume our total work as anything as per our convenience. The best assumption for easing out our calculations of the total work is assuming work as 100% or LCM of time taken by all the persons.
Points to Remember:
- Every work requires a particular amount of time.
- Work done is directly proportional to the time taken. And, the proportionality sign is removed by efficiency/one-day work/work rate.
Work done = Efficiency × Time taken
Let us understand the concept through a question
Example: The time taken by Ram and Shyam alone to complete a piece of work is 24 days and 40 days, respectively. What is the time taken by Ram and Shyam together to complete the same amount of work?
Solution:
Ram complete the whole work in 24 days
So, part of the work done by Ram in one day = 1/24
Shyam complete the whole work in 40 days
So, part of the work done by Shyam in one day = 1/40
Therefore, one day work of Ram and Shyam together will be
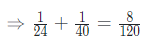
As Ram and Shyam together can complete 8/120 part of the work in 1 day
So, time taken by Ram and Shyam together to complete the work will be = 120/8=15 days
Alternative Method:
Step 1: Assuming a total work
Let us assume the total work be LCM of (24 and 40) = 120 units
Step 2: Calculating the efficiency of each individual
We know,
Work done = time taken × Efficiency(or one-day work)
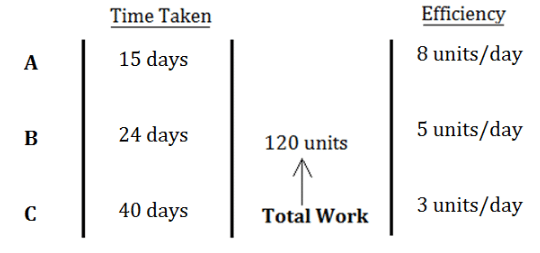
⇒ Efficiency of Ram = 120/24 = 5 units/day
⇒ Efficiency of Shyam = 120/40 = 3 units/day
You can depict the above-calculated information in the format shown below:
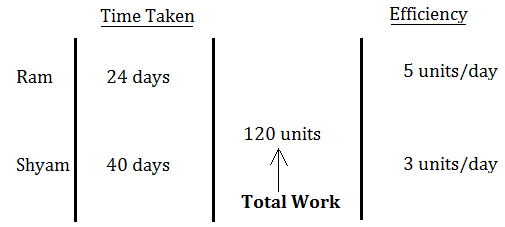
Step 3: Calculating the combined efficiency
From the above figure,
Efficiency of Ram and Shyam together will be = 5 + 3 = 8 units/day
Now,
time taken by Ram and Shyam to complete the work = Total work/ Efficiency = 120/8 = 15 days
Time and Work Questions
Example1. : Three men A, B, and C can complete a piece of work in 15, 24 and 40 days, respectively.
a. If A and B together have started the work and did work for 4 days, then the remaining work will be completed by C in how many days?
b. If A, B and C together have started the work, but 2 days after the start of work, A left the work while B left the work three days before the completion of the work, then in how many days total work gets completed?
Solution:
Let us assume the total work be LCM of (15, 24 and 40) = 120 units
Work done = time taken × Efficiency (or one-day work)
So,
a.
Here, it is given that A and B started the work together
So, efficiency of A and B together will be = 8 + 5 = 13 units/day
Now, the amount of work done by A and B together in 4 days will be = 13 * 4 = 52 units
Thus, remaining work = 120 – 52 = 68 units
As remaining work is to be done by only C
So, time taken by C to complete the remaining work will be
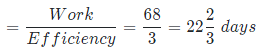
b.
Here, it is given that A, B and C together have started the work
So, efficiency of A, B and C together will be = 8 + 5 + 3 = 16 units/day
Amount of work done by A, B and C together in 2 days = 16 * 2 = 32 units
Now, remaining work = 120 – 32 = 88 units
As B left the work three days before the completion of the work
So, amount of work done by C in 3 days = 5 * 3 = 15 units
Thus, remaining work = 88 – 15 = 73 units
Here, we can say that the remaining work will be done by B and C together
Efficiency of B and C together will be = 5 + 3 = 8 units/day
Time taken by B and C together to complete the remaining 73 units of work
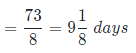
⇒ Total time taken to complete the work 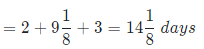
Note: If A working alone takes ‘d1’ days more than A and B together, and B working along takes ‘d2’ days more than A and B together, then the number of days taken by A and B working together will be 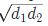
Example 2: - Brij alone takes 3 days more than Brij and Mohan together to complete work while Mohan takes 12 days more than Brij and Mohan together, then in how many days Brij and Mohan together can complete the work?
Solution: Here, d1 = 3 and d2 = 12
So, Time taken by Brij and Mohan to complete the work together will be 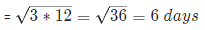
Concept of Efficiency
Efficiency denotes the amount of work done by any person in 1 day. We use this concept to compare the quality of a worker, i.e., if a worker is more efficient than any other worker, then we can say he/she can do more work in 1 day as compared to other workers.
The ratio of the efficiencies of two workers is inversely proportional to the time taken by them to complete a work.
- If a worker is less efficient than he/she will take more time to complete the work.
- If a worker is more efficient than he/she will take less time to complete the work.
- The number of workers is inversely proportional to the time taken to complete the work.
Example: - A is 3 times as efficient as B. If B alone can complete the work in 12 days, then A alone can complete the work in how many days?
Solution: - According to the question, the ratio of the efficiency of A and B is 3 : 1
We know that the ratio of the efficiency is inversely proportional to the ratio of the time taken
So, the ratio of the time taken by A and B to complete the work will be 1 : 3
Let us assume A alone completes the work in x days and B alone completes the work in 3x days
3x = 12
x = 4
Therefore, A alone can complete the work in 4 days.
Let us understand the application of the concept of efficiency through a question
Example: - 8 men and 7 women can complete a piece of work in 15 days while 6 men and 3 women can complete a piece of work in 30 days. In how many days 1 woman can complete the total work?
Solution: Let us assume efficiencies or one day work of 1 man and 1 woman are M and W respectively
So, the efficiency of 8 men = 8M and efficiency of 7 women = 7W
Similarly, efficiency of 6 men = 6M and efficiency of 3 women = 3W
We know,
Work done = time taken × Efficiency
According to question, 8 men and 7 women can complete a piece of work in 15 days
So, Total work done = (Efficiency of 8 men and 7 women) × Time taken
⇒ Total work done = (8M + 7W) * 15 = 120M + 105W …… (1)
Similarly, 6 men and 3 women can complete a piece of work in 30 days
So, Total work done = (Efficiency of 6 men and 3 women) × Time taken
⇒ Total work done = (6M + 3W) * 30 = 180M + 90W ….. (2)
As, total work done is same so
120M + 105W = 180M + 90W
60M = 15W
4M = 1W
From the above equation we can say that efficiency of 1 woman is equal to the efficiency of 4 men
Now, from equation (1)
Total work done = 120M + 105W
⇒ total Work done = 120/4 W + 150W = 135W
Therefore, time taken by 1 woman to complete the work will be
⇒ 135W/1W = 135 days
Work and Wages
The Concept of work and wages is used to compare the work with the remuneration for the work. The wages for any amount of work is directly proportional to the work done.
- If all the workers work for the same number of days, then their wages are in the ratio of their efficiencies.
- If all the workers have the same efficiencies and do the work for the different number of days, then their wages are distributed in the ratio of the number of days for which each of them worked.
- If the workers have different efficiency and do the work for the different number of days, then their wages are in the ratio of the work done by them.
MDH formula
MDH formula is used to compare the works of the same nature done at two different times using different manpower. The MDH formula can be represented as
Where M denotes the number of men/women, D denotes the number of days, H denotes the number of hours in a day, E denotes the efficiency of 1 man, and W denotes part of work done
Let us understand the application of this formula using a question
Example: - 20 men working 10 hours per day can finish 2/3rd of the work in 12 days, while 15 women working 9 hours per day can finish 2/5th of the work in X days. If one woman is twice as efficient as one man, then what is the value of X?
Solution:
Here,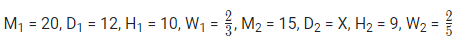
According to the question, one woman is twice as efficient as one man
So, the ratio of efficiency of woman and man is 2 : 1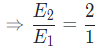
Now, using MDH formula we get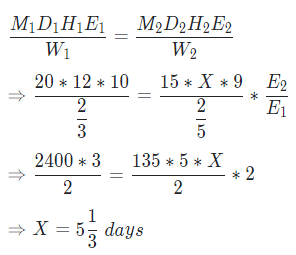
|
51 videos|172 docs|73 tests
|
FAQs on Time and Work: Shortcut & Tricks - Quantitative Techniques for CLAT
| 1. What is the concept of Time and Work? |  |
| 2. How is efficiency related to Time and Work? |  |
| 3. What is the concept of Work and Wages? |  |
| 4. What are some shortcuts and tricks to solve Time and Work problems? |  |
| 5. What are some frequently asked questions related to Time and Work in exams? |  |





















