Ratio and Proportions: Shortcuts & Tricks | Quantitative Techniques for CLAT PDF Download
What is Ratio?
It tells us about the relation between the two numbers.
Example: The ratio of A to B is 3:5.
This means Value of A/ Value of B = 3/5
What is Proportion?
It is the equality of two ratios. Many students often remain confused about the basic definition of Ratio & Proportion. Here we will try to clear that confusion.
A/B = 3/5 (This is the ratio of A to B)
Here, A is called the antecedent & B is called the consequent.
A/B = C/D (This is Proportion)
Proportion can also be written like,
a:b:: c:d in which Product of means= Product of extremes.
⇒ a×d = b×c
Compounded Ratio
If two or more ratios are given, then the ratio of the product of all antecedents to the product of all consequents is called compounded ratio.
Compounded Ratio of a:b, c:d, e:f will be, ace: bdf
Different Types of Proportion
Mean Proportion
a:M :: M:b, here M is the mean proportion of a & b.
M= √ab
Third Proportion
a:b :: b:T, here T is the third proportion of a & b.
T= b2/a
Fourth Proportion
a:b :: c:F, here F is the fourth proportion
F= (b×c)/a
Now let us try to understand some basic fundamentals of ratio that are usually used in questions asked in SSC exam through questions. We will also do some mixed problems of different topics involving the usage of ratio & proportion.
Examples
Q1: If A:B = 3:4, B:C = 7:8 then find A:B:C?
Sol: B is common to both, so make B equal. Multiply 1 with 7 & 2 with 4.
⇒ A:B=21:28, B:C= 28:32
Hence, A:B:C = 21:28:32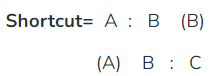
Write, the ratio in this format & then fill the blank spaces (mentioned with numbers in bracket) with the nearest number. Then, multiply vertically & you will get the answer.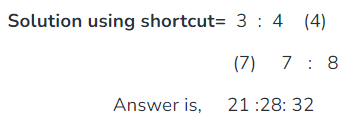
Q2: If ratio is given in reciprocals, A:B:C = 1/4 : 1/7 : 1/12. Convert it
Sol: Multiply the numerator with 4×7×12, we get
A : B : C = 7× 12 : 4× 12: 4×7 = 84: 48: 28 = 21: 12: 7
Q3: If the Ratio of A:B in a mixture is 4:9 and after adding 9 litres of liquid B the ratio now becomes 1:3. Find the original quantity if liquid A in the mixture?
Sol: A:B is 4:9, after adding 9 litres of new, the ratio is 1:3.
As only B is added, the quantity of A should remain the same. Making the quantity of A equal in both the ratios by multiplying second by 4, we get 4: 12.
Now, compare both the ratios for B, 12-9 units = 9 litres
⇒ 1 unit = 3 litres. Hence, 4 units, i.e quantity of liquid A is 12 litres.
Q4: The mean proportion of 9 & 25 is M. Third proportion of M & 15 is T. Find the fourth proportion of T, 18 & 30
Sol: M = √9×25 = 15
Third proportion of M & 15 = (15×15)/ 15 = 15 = T
Fourth proportion of T, 18 & 30 = (18 × 30)/ 15 = 36
Q5: 150 litres of a mixture contains milk & water in a ratio of 13:2. After the addition of some more milk to it, the ratio of milk to water now becomes 9:1. The quantity of milk that was added to the mixture was?
Sol: The concept to catch here is that water remains the same in both, so equate that in both ratios. We get, x = 5 units. 15 units = 150 L, so the water added is 50 litres.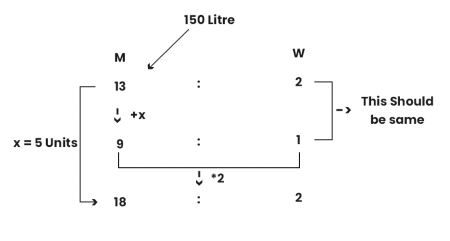
|
57 videos|108 docs|73 tests
|
FAQs on Ratio and Proportions: Shortcuts & Tricks - Quantitative Techniques for CLAT
| 1. What is the difference between ratio and proportion? |  |
| 2. How do you simplify a ratio? |  |
| 3. Can a ratio be negative? |  |
| 4. How can ratios be used in real-life situations? |  |
| 5. What are some common applications of proportions? |  |

|
Explore Courses for CLAT exam
|

|

















