Mensuration: Shortcuts & Tricks | Quantitative Techniques for CLAT PDF Download
Types of questions are given where this trick can be applied.
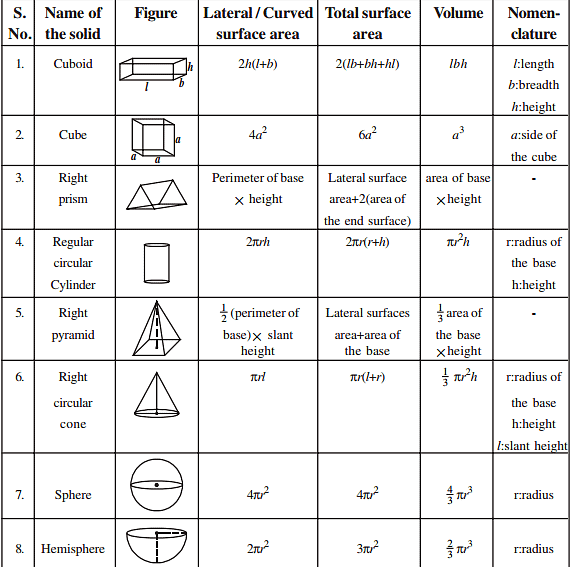
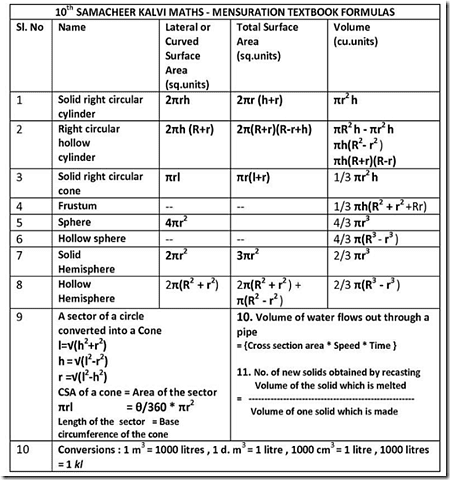
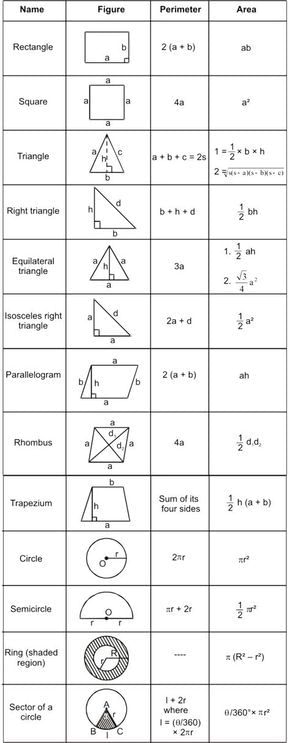
Use these Tricks
Direction: Check whether π=22/7 has been used in the formula for finding out the Particular Area, Curved Surface Area, Total Area, Volume, etc. If it is so, then
Q1: Find the surface area of a sphere whose volume is 4851 cubic meters.
(a) 1380 m2
(b) 1360 m2
(c) 1368 m2
(d) 1386 m2
Ans: d
Sol:
Using the Trick: We know that surface area of a sphere = 4πr2
It means ‘π’ has been used in finding out the surface area of the sphere.
We can easily see that only ‘1386’ from the given options is divisible by ‘11’
Hence, surface area of the sphere = 1386 m2
Q2: The radius and height of a right circular cylinder are 14 cm & 21 cm respectively. Find its volume.
(a) 12836 cm3
(b) 12736 cm3
(c) 12936 cm3
(d) 12837 cm3
Ans: c
Sol:
Using the Trick: The know that volume of Cylinder = πr2h
We must check divisibility by ‘11’. Here, both ‘12936’ and ‘12837’ are divisible by 11. But you also notice that radius (14 cm) & height (21 cm) are both multiples of 7. So the option divisible by ‘7’ is your answer.
Hence, volume of a right circular cylinder = 12936 cm3 (since this is the only option divisible by 7)
We can test this as follows:
Volume of the given cylinder
= (22/7) × 14 × 14 × 14 × 21 cm3
= 22 × 14 × 14 × 3 cm3
⇒ Volume must be divisible by ‘7’.
Q3: The radius and height of a right circular cone are 7 cm & 18 cm respectively. Find its volume.
(a) 814 cm3
(b) 624 cm3
(c) 825 cm3
(d) 924 cm3
Ans: d
Sol: Using the Trick:
The option should be divisible by ‘11’ because ‘π’ has been used in finding its volume. One of the parameters is a multiple of 7 without being a higher power. So we must go through fundamentals.
Now, volume of a right circular cone = (1/3)πr2h
= (1/3) × (22/7) × 7 × 7 × 18 cm3
= 22 × 7 × 6
Clearly, we need an answer that is a multiple of 11, 7 as well as 3.
Among the given options, 814, 825 and 924 are all multiples of 11. However, we see that only one option is divisible by 7. So this is the correct answer.
Hence, volume of the given cone = 924 cm3
|
49 videos|155 docs|73 tests
|
FAQs on Mensuration: Shortcuts & Tricks - Quantitative Techniques for CLAT
| 1. What are some shortcuts and tricks for solving mensuration problems? |  |
| 2. How can I quickly calculate the area of a circle? |  |
| 3. What is the trick to finding the surface area of a cube? |  |
| 4. How can I find the volume of a cylinder quickly? |  |
| 5. Are there any shortcuts for finding the volume of irregular shapes? |  |
















