Percentage: Shortcut & Tricks | Quantitative Techniques for CLAT PDF Download
Definition:
The percent is derived from the Latin word ‘Centum’ which means for ‘every 100’ or ‘per hundredth.’
“Percentage is the representation of a number, ratio, fraction, or decimal as a fraction of 100.”
Representing number, fraction, ratio and decimal in the form of Percentage
1. Number: To represent a number ‘N’ into Percentage, just simply multiply the number with 100.
Example: Convert ‘4’ into Percentage.
Sol: Representation of 4 in Percentage will be
= 4 × 100 = 400%
2. Fraction: To represent a fraction into Percentage, just simply multiply the fraction with 100 and to convert Percentage into fraction just simply divide the Percentage by 100.
Example: Convert the fraction 3/5 into Percentage
Sol: Representation of 3/5 into Percentage will be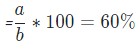
3. Ratio: To convert the ratio into Percentage, first convert the ratio into a fraction and then multiply the fraction with 100.
Example: Convert the ratio 2 : 5 into Percentage?
Sol: Converting ratio into fraction we get
Now, the representation of 2/5 into Percentage will be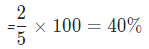
4. Decimal: To represent a decimal into Percentage just simply multiply the decimal with 100 and to convert Percentage into decimal just simply divide the Percentage by 100.
Example: Convert 0.773 into percentage
Sol: Representation of 0.773 into percentage will be
=0.773×100=77.3%0.773×100=77.3%
To solve the questions based on Percentage, one should learn some important conversion of Percentages into Fractions.
Let us represent some fractions in terms of Percentage in the tabular form for you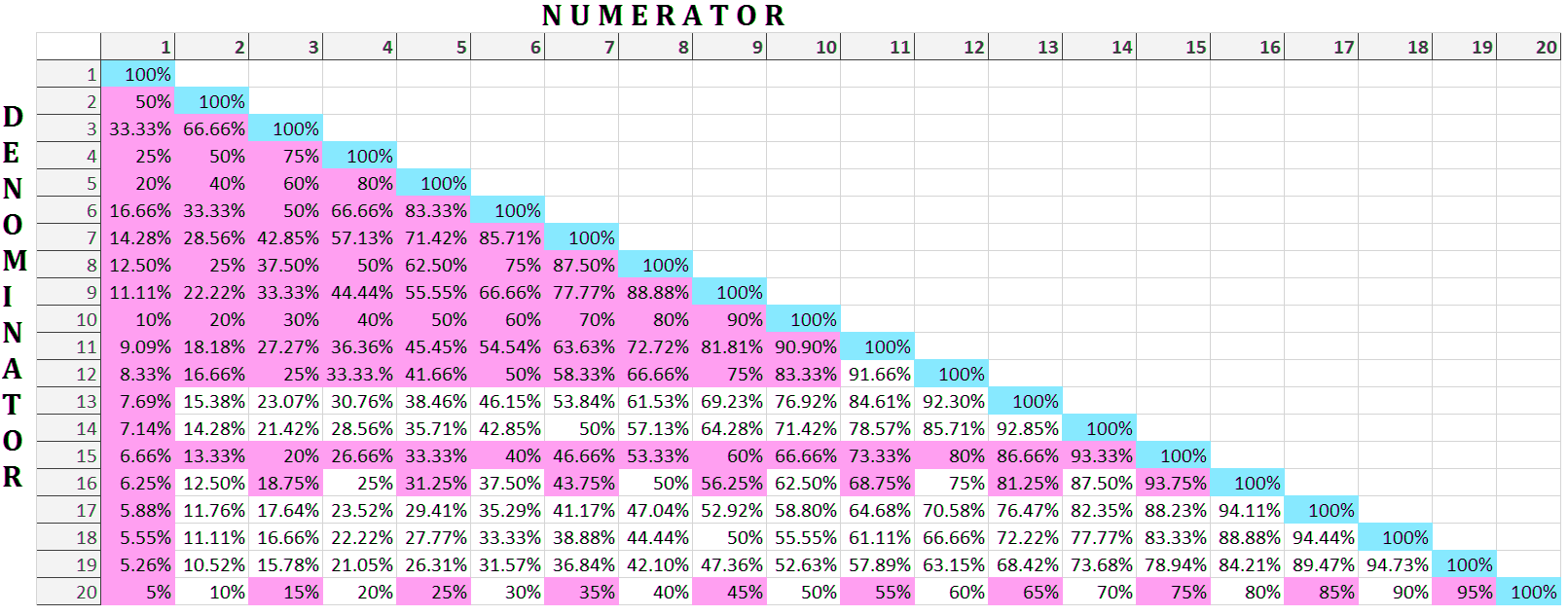
Some other important fraction values in terms of Percentage are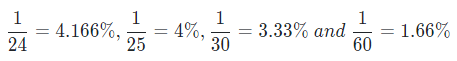
NOTE: learning all the important fractions will save you a lot of Time.
- If there is 0.11, 022, ……., 0.88, and 0.99 in the Percentage, then the fraction corresponding to the Percentage will have 9 or multiple of 9 in the denominator.
- If there is 0.33 and 0.66 in the Percentage, then the fraction corresponding to the Percentage will have 3 or multiple of 3 in the denominator.
- If there is 0.1428, 0.2856, 0.4285, 0.5713, 0.7142 and 0.8571 in the Percentage, then the fraction corresponding to the Percentage will have 7 or multiple of 7 in the denominator.
Increase/Decrease in Percentage
Percentage increase/decrease is the ratio of the change in number/quantity with respect to the original number/quantity.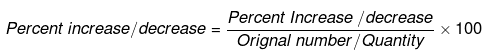
When A is increased by x%, then a new number B is obtained. To obtain the number A again, we have to decrease the number B by
When A is decreased by y%, then a new number B is obtained. To obtain the number A again, we have to increase the number B by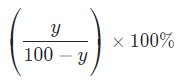
Let us understand the above concept through questions
Example: Raghu has 20% more toffee than Pinki. How much percent less toffees Pinki have as compared to Raghu?
Solution:
Here, the quantity of toffees with Raghu is 20% more than Pinki, i.e., the value of x is 20%
So, Percentage of toffees with Pinki as compared to Raghu will be less by: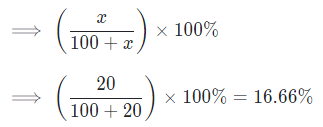
Note: When ‘percentage increased/decreased by X%’ is given for a quantity, then the actual increase/decrease in the quantity is (100±X%)
While when ‘percentage increase/decrease to X%’ is given for a quantity, then the actual increase/decrease in the quantity is (±X%)
For example, if the salary of a person is decreased by 20%, then the final salary of the person will be 80% of the original salary while if the salary of a person is decreased to 20% of the final salary of the person will be 20% of the original salary.
Concept of Product constancy
Product constancy involves the problems with two dependent quantities whose product is the third quantity. Thus, if there is an increase in the first quantity, then to make the third quantity constant, we have to increase/decrease the second quantity.
NOTE:
If there is an inverse relationship between the first and second quantity, then on the increase of the first quantity, we have to decrease the second quantity and vice versa.
- If there is an increase of x% in first quantity, then for the third quantity to remain constant, we have to decrease the second quantity by a factor
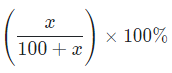
- If there is a decrease of y% in first quantity, then for the third quantity to remain constant, we have to increase the second quantity by a factor
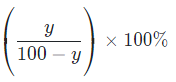
- If there is a direct relationship between first and second quantity, then on the increase/decrease of first quantity by x%, the second quantity will be increased/decreased by x%.
Some relations from which questions on product constancy are asked are:
- Expenditure = Price * Consumption
- Price = Rate * Quantity
- Distance = Speed * Time
- Work done = Time taken * Efficiency
- Area of Rectangle = Length * Breadth
Example: The price of sugar is increased by 25%. If a family does not want to increase/decrease their expenditure, then by what percent should it decrease their consumption?
Sol: We know, Expenditure = Price * Consumption
As, price is increased by 25%
So, here x = 25%
Thus, to remain the expenditure constant we should decrease the consumption by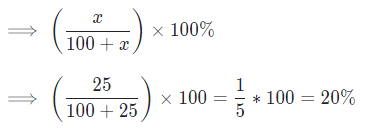
Quantities having relation in the form of C = A + B
In three quantities having a relation of C = A + B, quantity A is increased by x%. If we wish to maintain C as constant, then the B should be reduced by =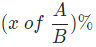 and vice versa in case of a decrease.
and vice versa in case of a decrease.
Example: The saving of a person is 20% of his income. If his expenditure increases by 10% without any increase in his income, then by how much percent he has to decrease his saving?
Solution:
Let us assume income of the person be 100
So, initial savings of the person = 20% of 100 = 20
We know, Income = Expenditure + Saving
Expenditure of person = 100 – 20 = 80
According to the question,
Final expenditure of person = 110% of 80 = 88
As, income is constant so final income = 100
Final Saving = 100 – 88 = 12
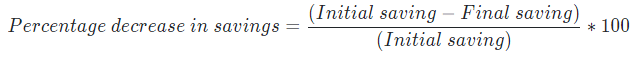
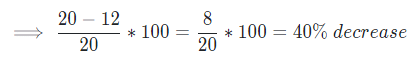
Successive Percentage increase/decrease
If a number N undergoes a successive percentage increase/decrease of a%, b%, c% and so on then after a net change in the number, the final value of number will be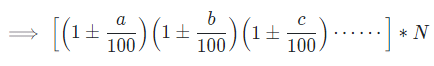
Application of Percentage on Population increase/decrease
If there is an r% increase/decrease in population of a place in a year, then
The Population of a place n years later will be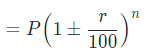
And, population of a place n years ago will be
And, population of a place n years ago will be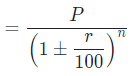
Type of questions asked from Percentage
Type 1: The population of a town increases by 20% each year. If the population of the town 3 years ago was 2500, then what is the present population of the town?
Sol: Let us assume the present population of the town is P
We know,
The population of a place n years ago will be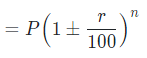
According to the question, 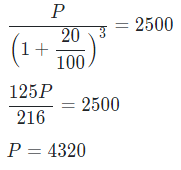
Thus, the present population of the town is 4320.
Type 2: In an examination, out of 400 students, 54% of boys and 70% of girls pass. If the total pass percentage was 60%. Find the total number of girls.
Sol: Let the number of girls be x
Thus, number of boys will be 400 – x
According to the question
Number of boys who pass = 54% of (400 – x)
Number of girls who pass = 70% of x
Total number of students who pass = 60% of 400
Thus,
60% of 400 = 54% of (400 – x) + 70% of x
240 = 216 – 0.54x + 07x
0.16x = 24
x = 150
Type 3: A salesman gets a 10% commission on the sales up to ₹ 25,000. On sales above ₹ 25,000, he gets a total commission of 15%. If he deposited a total sum of ₹ 86,250 in the company, then what will be the total earnings of the salesman?
Solution: If the company would have given 15% of commission instead of 10% on the sale up to ₹ 25000 also, then the company would receive some less amount which will be equal to
Loss of company = 5% of 25000 = ₹ 1250
The amount received by company = ₹ 86250
If the salesman would have given 15% of commission on all the sales, the amount received by the company will be
= ₹ 86250 - ₹1250 = ₹ 85000
We know,
15% = 3/20
Thus, on the sale of 20 units, he will earn 3 units
So, earnings of company will be = 20 – 3 = 17 units
Here, 17 units correspond to ₹ 85000
So, 1 unit will correspond to ₹ 5000
Now, earning of a salesman if he would have given 15% of the commission will be = 3 * 5000 = ₹15000But, in actual he has been given only 10% commission for starting ₹ 25,000
So, we can say that the actual earning of salesman = ₹ 15000 – ₹ 1250 = ₹13750
|
49 videos|179 docs|73 tests
|
FAQs on Percentage: Shortcut & Tricks - Quantitative Techniques for CLAT
| 1. What are some common shortcuts for calculating percentages? |  |
| 2. How can I calculate a percentage increase or decrease? |  |
| 3. What is the shortcut to calculate 20% of a number? |  |
| 4. How can I calculate a percentage of a percentage? |  |
| 5. Is there a shortcut to find 75% of a number? |  |





















