Class 5 Maths Chapter 7 Important Question Answers - Chapter 7 - Can you see the pattern
Q1: Construct a 5 × 5 magic square using all even number from 1 to 50
Ans: Using all the even numbers from 1 to 50 , a 3 × 3 magic square is constructed as shown above:
Considering the above drawn magic square, the magic sum is 26 × 5 = 130.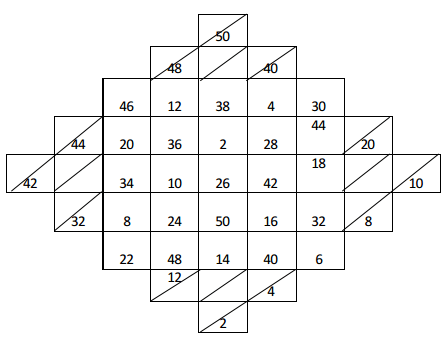
Q2: Using the numbers from 5 to 13 , construct a 3 × 3 magic square. What is the magic sum here? What relation is there between the magic sum and the number in the central cell?
Ans: Using the numbers from 5 to 13 , a 3 × 3 magic square is constructed as shown above:
Considering the above drawn magic square, the magic sum is 9 × 3 = 27 .
Hence, the relation between the magic sum and the number in the central cell is that if we multiply the middle number to 3 (middle number × 3), then we get the magic sum.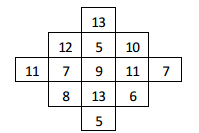
Q3: Construct a 3 × 3 magic square using all odd number from 1 to 17
Ans: Using all the odd numbers from 1 to 17, a 3 × 3 magic square is constructed as shown above:
Considering the above drawn magic square, the magic sum is 9 × 3 = 27.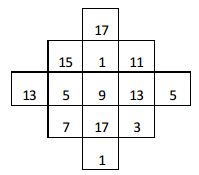
Q4: Starting with the middle cell in the bottom row of the square and using numbers from 1 to 9, construct a 3 × 3 magic square
Ans: Using the numbers from 1 to 9, a 3 × 3 magic square is constructed as shown above:
Considering the above drawn magic square, the magic sum is 5 × 3 = 15.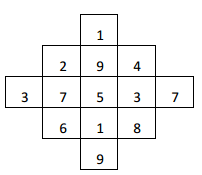
Q5: Write an algorithm to check if a number is even or odd, using both pseudocode and flowchart.
Ans: pseudocode:
take Number
remainder = Number%2
if remainder==0;
print even
else
print odd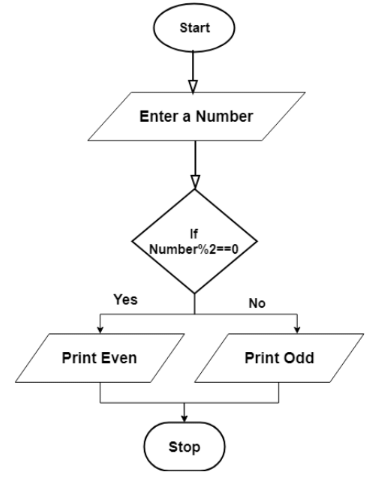
Q6: What relation is there between the magic sum and the number in the central cell?
Ans: (1) If we take sum of numbers in any row, in any column and in any diagonal, it comes up to be 27
(2) Number in the central cell is 9
(3) 9 × 3 = 27
Thus, we can say that magic sum is three times the number in the central cell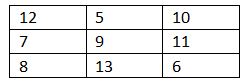
Q7: Construct a 5 × 5 magic square using all even numbers from 1 to 50.
Ans: As shown in the figure, magic sum is 130
Number in the central cell is 26
26 × 5 = 120
Thus, magic sum is five times the number in central cell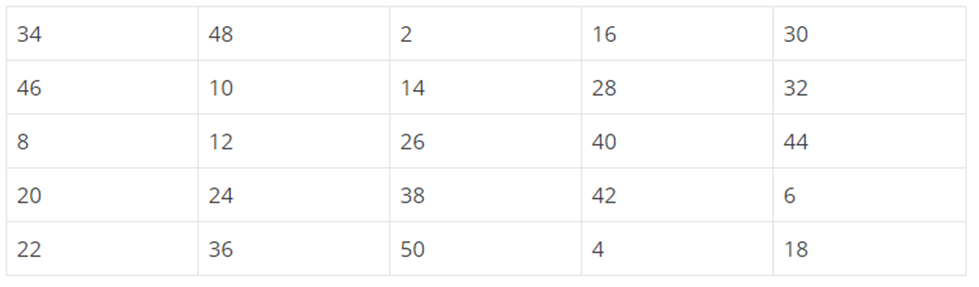
Q8: Complete the following magic square:
Ans: Row wise sum is as follows:
4 + 9 + 8 = 21,
11 + 7 + 3 = 21,
6 + 5 + 10 = 21.
Column wise sum is as follows:
4 + 11 + 6 = 21,
9 + 7 + 5 = 21,
8 + 3 + 10 = 21.
Diagonal wise sum is as follows:
4 + 7 + 10 = 21,
8 + 7 + 6 = 21.
Hence, the magic square is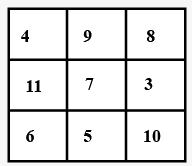
Q9: Starting with the middle cell in the bottom row of the square and "using numbers from 1 to 9 construct a 3 × 3 magic square.
Ans: Figure shows 3 × 3 magic square in which magic sum is 15 and central cell contains 5
We know that 5 × 3 = 15
Thus, magic sum is 3 times the number in central cell.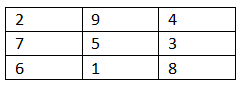
Q10: Solve the following riddles, you may yourself construct such riddles. Who am I?
Go round a square counting every corner Thrice and no more! Add the count to me To get exactly thirty-four!
Ans: There are 4 comers in a square
Thrice the number of comers in the square will be 3 × 4 = 12
When this result i,e 12 , is added to the number if Comes to be 34 . therefore the number will be the difference of 34 and 12 i.e 34 − 12 = 22.
|
31 videos|290 docs|45 tests
|
FAQs on Class 5 Maths Chapter 7 Important Question Answers - Chapter 7 - Can you see the pattern
| 1. What is the pattern in Class 5? |  |
| 2. How do you identify patterns in Class 5? |  |
| 3. Why is it important to understand patterns in Class 5? |  |
| 4. Can you provide an example of a pattern in Class 5? |  |
| 5. How can patterns be applied in real-life situations for Class 5 students? |  |
















