NEET Exam > NEET Notes > Physics Class 12 > Important Derivations: Electrostatic Potential and Capacitance
Important Derivations: Electrostatic Potential and Capacitance | Physics Class 12 - NEET PDF Download
Derivations Related to Potential due to an Electric Dipole
Derivation 1: Electric potential due to electric dipole at a point on its axial line.
Sol: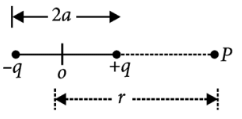
Let ‘P’ be an axial point at distance ‘r’ from the centre of the dipole. Electric potential at point P will be
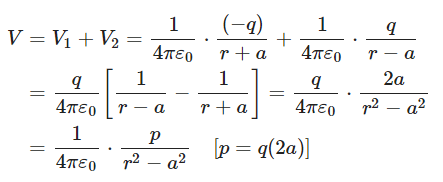For a far away point, r>>a
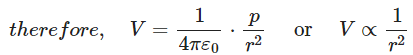Thus, due to a dipole potential at a point is
Derivations Related to Potential Energy of System of Charges
Derivation 2: Expression for electric potential energy of a system of three charges
Sol: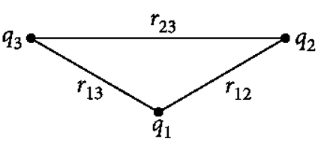 
To bring q1 from infinity to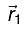 
, no work is required. Work done is bringing charge q2 from infinity to 
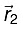is
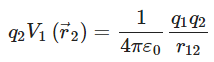
The charges q1 and q2 produce a potential, which at any point p is given by
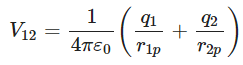Work done next in bringing q3 from infinity to the point 
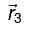is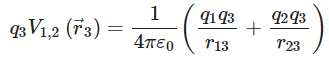
The total work done in assembling the charges at the given location is obtained by adding the work done in steps (i) and (ii) is
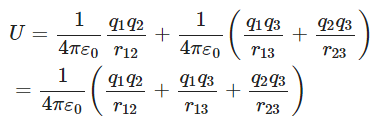
The document Important Derivations: Electrostatic Potential and Capacitance | Physics Class 12 - NEET is a part of the NEET Course Physics Class 12.
All you need of NEET at this link: NEET
74 videos|330 docs|92 tests |
FAQs on Important Derivations: Electrostatic Potential and Capacitance - Physics Class 12 - NEET
| 1. What is the electric potential due to an electric dipole? |  |
Ans. The electric potential due to an electric dipole at a point in space is given by the equation V = k * p * cosθ / r^2, where V is the electric potential, k is the electrostatic constant, p is the magnitude of the dipole moment, θ is the angle between the dipole moment and the line connecting the point to the dipole, and r is the distance between the point and the dipole.
| 2. How can the potential energy of a system of charges be calculated? | |
Ans. The potential energy of a system of charges can be calculated by using the equation U = k * q1 * q2 / r, where U is the potential energy, k is the electrostatic constant, q1 and q2 are the magnitudes of the charges, and r is the distance between the charges.
| 3. What are some important derivations related to electrostatic potential and capacitance? | |
Ans. Some important derivations related to electrostatic potential and capacitance include the derivation of the formula for the electric potential due to a point charge, the derivation of the formula for the electric potential due to an electric dipole, the derivation of the formula for the electric potential due to a uniformly charged spherical shell, and the derivation of the formula for the capacitance of a parallel plate capacitor.
| 4. How is the electric potential due to a point charge derived? | |
Ans. The electric potential due to a point charge can be derived by considering the work done to bring a test charge from infinity to a point in the electric field of the point charge. By integrating the work done formula, which is given by W = q * V, where W is the work done, q is the test charge, and V is the electric potential, the equation V = k * q / r can be derived, where k is the electrostatic constant and r is the distance between the point charge and the test charge.
| 5. What is the formula for the capacitance of a parallel plate capacitor? | |
Ans. The formula for the capacitance of a parallel plate capacitor is given by C = ε * A / d, where C is the capacitance, ε is the permittivity of the material between the plates, A is the area of each plate, and d is the distance between the plates.
About this Document
4.69/5 Rating
Feb 07, 2026 Last updated
Document Description: Important Derivations: Electrostatic Potential and Capacitance for NEET 2026 is part of Physics Class 12 preparation. The notes and questions for Important Derivations: Electrostatic Potential and Capacitance have been prepared according to the NEET exam syllabus. Information about Important Derivations: Electrostatic Potential and Capacitance covers topics like and Important Derivations: Electrostatic Potential and Capacitance Example, for NEET 2026 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Important Derivations: Electrostatic Potential and Capacitance.
Introduction of Important Derivations: Electrostatic Potential and Capacitance in English is available as part of our Physics Class 12 for NEET & Important Derivations: Electrostatic Potential and Capacitance in Hindi for Physics Class 12 course. Download more important topics related with notes, lectures and mock test series for NEET Exam by signing up for free. NEET: Important Derivations: Electrostatic Potential and Capacitance | Physics Class 12 - NEET
Description
Full syllabus notes, lecture & questions for Important Derivations: Electrostatic Potential and Capacitance | Physics Class 12 - NEET - NEET | Plus exercises question with solution to help you revise complete syllabus for Physics Class 12 | Best notes, free PDF download
Information about Important Derivations: Electrostatic Potential and Capacitance
In this doc you can find the meaning of Important Derivations: Electrostatic Potential and Capacitance defined & explained in the simplest way possible. Besides explaining types of Important Derivations: Electrostatic Potential and Capacitance theory, EduRev gives you an ample number of questions to practice Important Derivations: Electrostatic Potential and Capacitance tests, examples and also practice NEET tests
Related Searches
Extra Questions, Objective type Questions, mock tests for examination, study material, pdf , Previous Year Questions with Solutions, Sample Paper, Semester Notes, Viva Questions, Important questions, MCQs, Important Derivations: Electrostatic Potential and Capacitance | Physics Class 12 - NEET, Summary, past year papers, Important Derivations: Electrostatic Potential and Capacitance | Physics Class 12 - NEET, Free, ppt, Important Derivations: Electrostatic Potential and Capacitance | Physics Class 12 - NEET, Exam, video lectures, shortcuts and tricks, practice quizzes;