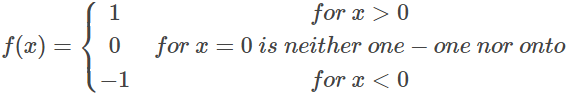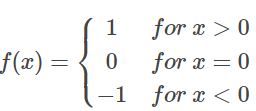Q1: Let A = R {3} and B = R – {1}. Consider the function f: A →B defined by f (x) = (x- 2)/(x -3). Is f one-one and onto? Justify your answer.
Ans: Given function:
f (x) = (x- 2)/(x -3)
Checking for one-one function:
f (x1) = (x1– 2)/ (x1– 3)
f (x2) = (x2-2)/ (x2-3)
Putting f (x1) = f (x2)
(x1-2)/(x1-3)= (x2-2 )/(x2 -3)
(x1-2) (x2– 3) = (x1– 3) (x2-2)
x1 (x2– 3)- 2 (x2 -3) = x1 (x2– 2) – 3 (x2– 2)
x1 x2 -3x1 -2x2 + 6 = x1 x2 – 2x1 -3x2 + 6
-3x1– 2x2 =- 2x1 -3x2
3x2 -2x2 = – 2x1 + 3x1
x1= x2
Hence, if f (x1) = f (x2), then x1 = x2
Thus, the function f is one-one function.
Checking for onto function:
f (x) = (x-2)/(x-3)
Let f(x) = y such that y B i.e. y ∈ R – {1}
So, y = (x -2)/(x- 3)
y(x -3) = x- 2
xy -3y = x -2
xy – x = 3y-2
x (y -1) = 3y- 2
x = (3y -2) /(y-1)
For y = 1, x is not defined But it is given that. y ∈ R – {1}
Hence, x = (3y- 2)/(y- 1) ∈ R -{3} Hence, f is onto.
Q2: Let A = N × N and * be the binary operation on A defined by (a, b) * (c, d) = (a + c, b + d). Show that * is commutative and associative. Find the identity element for * on A, if any.
Ans: Check the binary operation * is commutative:
We know that, * is commutative if (a, b) * (c, d) = (c, d) * (a, b) ∀ a, b, c, d ∈ R
L.H.S =(a, b) * (c, d)
=(a + c, b + d)
R. H. S = (c, d) * (a, b)
=(a + c, b + d)
Hence, L.H.S = R. H. S
Since (a, b) * (c, d) = (c, d) * (a, b) ∀ a, b, c, d ∈ R
* is commutative (a, b) * (c, d) = (a + c, b + d)
Check the binary operation * is associative :
We know that * is associative if (a, b) * ((c, d) * (x, y)) = ((a, b) * (c, d)) * (x, y) ∀ a, b, c, d, x, y ∈ R
L.H.S = (a, b) * ( (c, d) * (x, y) ) = (a+c+x, b+d+y)
R.H.S = ((a, b) * (c, d)) * (x, y) = (a+c+x, b+d+y)
Thus, L.H.S = R.H.S
Since (a, b) * ( (c, d) * (x, y) ) = ((a, b) * (c, d)) * (x, y) ∀ a, b, c, d, x, y ∈ R
Thus, the binary operation * is associative
Checking for Identity Element:
e is identity of * if (a, b) * e = e * (a, b) = (a, b)
where e = (x, y)
Thus, (a, b) * (x, y) = (x, y) * (a, b) = (a, b) (a + x, b + y)
= (x + a , b + y) = (a, b)
Now, (a + x, b + y) = (a, b)
Now comparing these, we get:
a+x = a
x = a -a = 0
Next compare: b +y = b
y = b-b = 0
Since A = N x N, where x and y are the natural numbers. But in this case, x and y is not natural number. Thus, the identity element does not exist.
Therefore, operation * does not have any identity element.
Q3: Show that the Signum Function f: R → R, given by
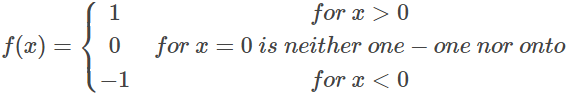
Ans: Check for one to one function:
For example:
f(0) = 0
f(-1) = -1
f(1) = 1
f(2) = 1
f(3) = 1
Since, the different elements say f(1), f(2) and f(3), shows the same image, then the function is not one to one function.
Check for Onto Function:
For the function, f: R →R
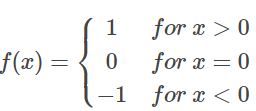
In this case, the value of f(x) is defined only if x is 1, 0, -1For any other real numbers(for example y = 2, y = 100) there is no corresponding element x.
Thus, the function “f” is not onto function.
Hence, the given function “f” is neither one-one nor onto.
Q4: Let f : N → Y be a function defined as f (x) = 4x + 3, where, Y = {y ∈ N: y = 4x + 3 for some x ∈ N}. Show that f is invertible. Find the inverse.
Ans: Checking for Inverse:
f(x) = 4x + 3
Let f(x) = y
y = 4x + 3
y – 3 = 4x
4x = y – 3
x = (𝑦 − 3)/4
Let g(y) = (𝑦 − 3)/4
where g: Y → N
Now find gof:
gof= g(f(x))
= g(4x + 3) = [(4𝑥 + 3) − 3]/4
= [4𝑥 + 3 − 3]/4
=4x/4
= x = IN
Now find fog:
fog= f(g(y))
= f [(𝑦 − 3)/4]
=4[(𝑦 − 3)/4] +3
= y – 3 + 3
= y + 0
= y = Iy
Thus, g of = IN and fog = Iy,
Hence, f is invertible
Also, the Inverse of f = g(y) = [𝒚 – 3]/ 4
Q5: If f: R → R is defined by f(x) = x2 − 3x + 2, find f(f(x)).
Ans: Given function:
f(x) = x2 − 3x + 2.
To find f(f(x))
f(f(x)) = f(x)2 − 3f(x) + 2.
= (x2 – 3x + 2)2 – 3(x2 – 3x + 2) + 2
By using the formula (a-b+c)2 = a2 + b2 + c2-2ab +2ac-2ab, we get
= (x2)2 + (3x)2 + 22– 2x2 (3x) + 2x2(2) – 2x2(3x) – 3(x2 – 3x + 2) + 2
Now, substitute the values
= x4 + 9x2 + 4 – 6x3 – 12x + 4x2 – 3x2 + 9x – 6 + 2
= x4 – 6x3 + 9x2 + 4x2 – 3x2 – 12x + 9x – 6 + 2 + 4
Simplify the expression, we get,
f(f(x)) = x4 – 6x3 + 10x2 – 3x