Worksheet: Units and Measurements | Physics Class 11 - NEET PDF Download
Section A. Fill in the Blanks
Q1: The standard unit of time in the International System of Units (SI) is ____________.
Q2: The diameter of a circle is a ___________ quantity.
Q3: The Vernier scale is used for measuring ________.
Q4: The dimensions of the coefficient of viscosity (η) are _________.
Q5: The precision of a measurement is determined by the number of ____________.
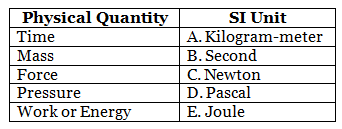
Section B. Match the Column
Section C. Multiple Choice Questions
Q1: Which of the following is a base unit in the International System of Units (SI)?
(a) Newton
(b) Kilogram
(c) Joule
(d) Pascal
Q2: The least count of a Vernier caliper is 0.01 cm. If the main scale reading is 2.3 cm and the Vernier scale reading is 0.08 cm, the correct measurement is:
(a) 2.31 cm
(b) 2.32 cm
(c) 2.38 cm
(d) 2.4 cm
Q3: The dimension of speed is:
(a) [M0L1T-1]
(b) [M0L0T-1]
(c) [M-1L0T-1]
(d) [M1L1T-1]
Q4: Which of the following is not a derived unit?
(a) Newton (N)
(b) Meter (m)
(c) Watt (W)
(d) Pascal (Pa)
Q5: A car travels a distance of 400 meters in 20 seconds. What is its average speed?
(a) 20 m/s
(b) 40 m/s
(c) 5 m/s
(d) 2 m/s
Section D. Assertion Reason
Q1: Assertion: The dimensions of angular velocity are [M0L0T-1].
Reason: Angular velocity is a scalar quantity.
Q2: Assertion: Two physical quantities having the same dimensions are always equal. Reason: Dimensions are just labels and do not affect the numerical value of a quantity.
Section E. Case Based Questions
Case 1: A student measures the length of a pencil using two different rulers. Ruler A has a least count of 0.1 cm, and ruler B has a least count of 0.01 cm. The student obtains measurements of 7.2 cm using ruler A and 7.25 cm using ruler B. Calculate the percentage error in each measurement and discuss the precision of each ruler.
Case 2: A student measures the time taken for a pendulum to complete 10 oscillations. He records three sets of measurements as follows: 14.5 s, 14.3 s, and 14.4 s. Calculate the mean time and the absolute error in the measurement.
Section F. Short Answer Type
Q1: Define dimensional analysis. How is it useful in physics? (Word Limit: 100-120 words)
Q2: Explain the difference between precision and accuracy in measurements. (Word Limit: 100-120 words)
Q3: Differentiate between scalar and vector quantities with examples. (Word Limit: 100-120 words)
Q4: State and explain the principle of the Vernier caliper. (Word Limit: 100-120 words)
Q5: Explain the concept of relative error in measurements. (Word Limit: 100-120 words)
Section G. Long Answer Type
Q1: Discuss the importance of units and measurements in scientific research. (Word Limit: 150-200 words)
Q2: Explain the principle of the Vernier scale in detail and provide a step-by-step procedure for using a Vernier caliper to measure the length of an object. (Word Limit: 150-200 words)
Q3: Explain the concept of significant figures in measurements. Provide examples of how to determine the number of significant figures in various measurements. (Word Limit: 150-200 words)
Q4: Discuss the process of dimensional analysis with an example. (Word Limit: 150-200 words)
Q5: Explain the concept of the International System of Units (SI) and its importance in scientific measurements. Provide examples of SI units for various physical quantities. (Word Limit: 150-200 words)
Section H. Numericals
Q1: Find the dimensions of (a/b) in the equation:  where P is pressure, x is distance and t is time.
where P is pressure, x is distance and t is time.
Q2: Find an expression for viscous force F acting on a tiny steel ball of radius r moving in a viscous liquid of viscosity η with a constant speed ν by the method of dimensional analysis.
Q3: Suppose there existed a planet that went around the sun twice as fast as the earth. What would be its orbital size as compared to that of the earth?
Q4: A great physicist of this century (P.A.M. Dirac) loved playing with numerical values of Fundamental constants of nature. This led him to an interesting observation. Dirac found that from the basic constants of atomic physics (c, e, mass of electron, mass of proton) and the gravitational constant G, he could arrive at a number with the dimension of time. Further, it was a very large number, its magnitude being close to the present estimate on the age of the universe (15 billion years). From the table of fundamental constants in the book, try to see if you too can construct this number (or any other interesting number you can think of). If its coincidence with the age of the universe were significant, what would this imply for the constancy of fundamental constants?
You can access the solutions to this worksheet here.
|
119 videos|494 docs|98 tests
|
FAQs on Worksheet: Units and Measurements - Physics Class 11 - NEET
| 1. What are the basic units of measurement in the metric system? |  |
| 2. How do you convert between different units of measurement? |  |
| 3. What is the difference between mass and weight? |  |
| 4. Why is it important to use standard units of measurement? |  |
| 5. How can I measure irregular objects accurately? |  |





















