Overview: Mixture & Alligations | Quantitative Techniques for CLAT PDF Download

Mixture and Alligation

Mixture and Alligation: Quantitative Aptitude is a very important section for government recruitment exams like SSC, railway, and banking. In this article, we are going to discuss one of the most important topic of the quantitative aptitude section i.e. rule of mixtures and alligations. Mixture and alligation is a mathematical technique used to solve problems related to mixing different ingredients or components at different ratios to obtain a desired mixture with a specified property (e.g., concentration, price, etc.). The rule of alligation enables us to find the ratio in which two or more ingredients at the given price must be mixed to produce a mixture of the desired price.

• Mixture: An aggregate of two or more two types of quantities gives us a mixture.
• Alligation: It is a method of solving arithmetic problems related to mixtures of ingredients. This rule enables us to find the ratio in which two or more ingredients at the given price must be mixed to produce a mixture of the desired price.
  

Formula Of Mixture and Alligation

It is a modified form of finding the weighted average. If 2 ingredients are mixed in a ratio and the cost price of the unit quantity of the mixture, called the Mean Price is given then,

The above formula can be represented with the help of a diagram which is easier to understand. Here ‘d’ is the cost of a dearer ingredient, ‘m’ is the mean price, and ‘c’ is the cost of a cheaper ingredient.

Quantity of Cheaper element /Quantity of Dearer element = CP of 1 unit of dearer element – Mean Price /Mean Price CP of 1 unit of cheaper element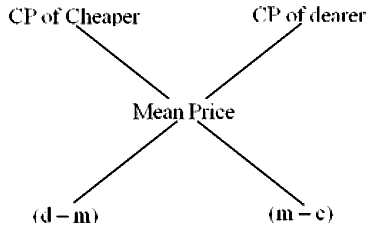

Thus, (Cheaper quantity) : (Dearer quantity) = (d – m) : (m – c).

Example 1: A container contains 40 liters of milk. From this container, 4 liters of milk were taken out and replaced by water. This process was repeated further two times. How much milk is now contained in the container?
(a) 26 liters
(b) 29.16 liters
(c) 28 liters
(d) 28.2 litres
Ans: (c)
Sol: Assume that a container contains x of liquid from which y units are taken out and replaced by water. After n operations, the quantity of pure liquid =x(1-y/x)ⁿ
Hence milk now contained by the container = 40(1-4/40)³ =40(1-1/10)³
=40×9/10×9/10×9/10 =(4×9×9×9)/100 =29.16

Example 2: A vessel is filled with liquid, 3 parts of which are water and 5 parts syrup. How much of the mixture must be drawn off and replaced with water so that the mixture may be half water and half syrup?
(a) 1/3
(b) 1/4
(c) 1/5
(d) 1/7
Solution: (c)
Suppose the vessel initially contains 8 liters of liquid.
Let x liters of this liquid be replaced with water.
Quantity of water in new mixture = (3 – 3x/8 + x) litre
Quantity of syrup in new mixture = (5 – 5x/8) litres
So  (3 – 3x/8 + x)  = (5 – 5x/8) litres
⇒ 5x + 24 = 40 – 5x
⇒10x = 16
⇒ x = 8/5 .So, part of the mixture replaced = (8/5 x 1/8) = 1/5