Overview: Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT PDF Download
What are Cubes?
Suppose a number is raised to power 3. Then, we call it a cube of that number. In other words, if a number multiplies itself 3 times, then we call it a cube of that number.
Example: 23 = 2 × 2 × 2 = 8
⇒ The cube of 2 is 8 .
Cubes of Natural Numbers
The cube of a natural number is that natural number raised to power 3.
Thus, if n is a natural number, then, n3 is the cube of n , and we have n3 = n × n × n
Perfect Cube Numbers
A number is a perfect cube if it is a cube of some natural number.
Example: 27 is a perfect cube because there is a natural number 3 such that 27 = 3 × 3 × 3. But, 12 is not a perfect cube because there is no natural number whose cube is 12.
There are only 10 perfect cubes from 1 to 1000 . They are listed below.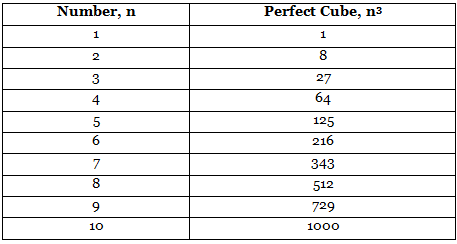
Properties of Cubes of Natural Numbers
- Cubes of all even natural numbers are even.
- Cubes of all odd numbers are odd.
- The sum of the cubes of first n natural numbers is equal to the square of their sum.
That is, 13 + 23 + 33 +……+ n3 = (1 + 2 + 3 +……+n)2 Cubes of the numbers ending in digits 4, 5, 6 and 9 are the numbers ending in the same digit. - Cubes of numbers ending in digit 2 ends in digit 8 , and the cube of numbers ending in digit 8 ends in digit 2 . The cubes of the numbers ending in digits 3 and 7 ends in digits 7 and 3 , respectively.
- If a prime number p divides m , then p × p × p will divide m × m × m , i.e., p3 will divide m3. Thus, if a prime number p divides a perfect cube, then p3 also divides this perfect cube.
Finding Cube of a Two-Digit Number by Column Method
This method is based upon an old Indian practice of multiplying two numbers. It is convenient for finding squares of two-digit numbers only. As the number of digits increases, this method becomes difficult and time-consuming. So, we shall discuss it for two-digit numbers only.
This method uses the identity (a+b)3 = a3+ b3 + 3a2b + 3ab2 for finding the cube of the two-digit number ab where a is the tens digit and b is the units digit, be a two-digit natural number.
Example: Find a cube of 42 by using the column method.
Sol: Let a = 4 and b = 2
- Step 1: Make four columns and write the values of a3, 3a2b, 3ab2 and b3 respectively in these columns.
- Step 2: Underline the unit digits of b3 and add its tens digit, if any, to column III.
- Step 3: Underline the unit digits of 3ab2 and add its tens digit, if any, to column II
- Step 4: Underline the unit digits of 3a2b and add its tens digit, if any, to column I.
- Step 5: Underline the number in column I.
- Step 6: Write the underlined digits at the bottom of each column to obtain the cube of the given number.

Therefore, 423 = 74088
Cubes of Negative Integers
The cube of a negative integer is always negative. In general, if m is a positive integer, then:
(−m)3= −m × −m × −m
Example: (−2)3 = −2 × −2 × −2 = −8
Cubes of Rational Number
Let a = m/n be a rational number, where m and n are non-zero integers, then a cube of a is defined as a3 = a × a × a or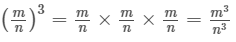
A number m is the cube root of a number n if n = m3. In other words, the cube root of a number n is that number m whose cube gives n.
The cube root of a number n is denoted by ∛n. ∛n is also called a radical, n is called the radicand, and 3 is called the radical index.
The below table provides all the cube roots upto 1000.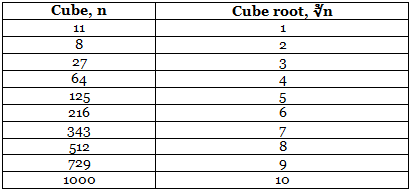
Cube Roots Formula
The cube root formula is used to find the cube root of any number stated in radical form with the sign ∛3.
Cube Root of Natural Numbers
A natural number m is the cube root of a natural number n if n = m3 and we write it as ∛n = m
Cube Root of a Number Using Its One’s Place
The units digit of a cube of a natural number depends upon the unit digit of the given number. The following are the rules to be followed, they are;
- Look at the digit at the units place and determine the digit at the units place in the cube root.
- Make groups of three digits, beginning with an extreme right digit of the given number. For example, we can group 15625 as 15625.
- The first group will be 625 and the second group will be 15. See the digit at the unit’s place in the first group of three digits in the given number and then identify the digit at the unit’s place in the given number’s cube root using the following table.

- So, the unit place of 15625 will be 5 as the unit place in the first group of three digits of 15625 is 5. Strikeout units, tens and hundreds places digits. If no digits are left out, then the digit obtained in step 2 is the required cube root. If digit/digits are left out, proceed further.
- Consider the number left after striking out the three digits in step 2. Identify the largest one-digit number whose cube is less than or equal to this left-out number. This digit will be the tens digit of the required cube root. The number left out in 15625 is 15.
The largest one-digit number whose cube is less than or equal to 12 is 23 = 8. - Now write down the number whose units digit is the number obtained in step 1 and the tens digit is the number obtained in step 3 , then write the required cube root. So,
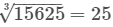
Example: Let us find the cube root of 64 by the method mentioned above.
Sol: In the given number 64 , the unit’s place is 4. Therefore, the digit at the one’s place in the cube root is 4 . Since no number is left after striking out the units and ten’s digit of the number. Therefore, the required cube root is 4 . i.e. ∛64 = 4
Cube Root of a Perfect Cube by Factors
We use the below steps to find the cube root of a perfect cube by factors.
- Obtain the given number
- Resolve it into prime factors
- Group the factors in triples such that all the three factors in each triple are equal.
- Take one factor from each triplet formed in the third step.
- Find the product of factors obtained in the above step. This product is the required cube root.
Cube Root of Product of Integers
For any two integers a and b , we have 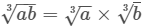
Cube Root of a Rational Number
If x and a are two rational numbers such that x3 = a , then we say that x is the cube root of a and we write it as ∛a =x.
In other words, for any rational number a/b, we have 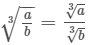
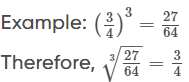
|
49 videos|179 docs|73 tests
|
FAQs on Overview: Squares, Square Roots, Cubes, Cube Roots - Quantitative Techniques for CLAT
| 1. What are cubes? |  |
| 2. What are cubes of natural numbers? |  |
| 3. What are perfect cube numbers? |  |
| 4. How can we find the cube of a two-digit number using the column method? |  |
| 5. What is the relationship between squares, square roots, cubes, and cube roots? |  |
















