Overview: Unitary Method | Quantitative Aptitude for SSC CGL PDF Download
| Table of contents |

|
| Unitary Method |

|
| Types of Unitary Method |

|
| Steps to use Unitary Method |

|
| Unitary Method in Ratio and Proportion |

|
| Uses of Unitary Method |

|
Unitary Method
Definition of Unitary Method : Unitary Method is a mathematical process to calculate the value of a single unit from the value of multiple units and the value of multiple unit rate from the value of a single unit.
- It is a numerical process that we use to calculate any value i.e., cost or speed or anything, of any desired quantity.
- The primary condition to use this method is that we should be provided with the value of certain quantities, and then we can use the Unitary Method to calculate the value of desired quantity.
Example 1: If we have been provided with data where it is said that 3 students can together complete a group project within 5hrs, and we need to calculate how many hours it is required to complete that project if the group has 5 students.
Sol: Here we have a value of a certain quantity i.e., 3 students need 5 hrs to complete, and we need to find the value for a desired quantity i.e., number of hours required by 5 students.
So we can use the Unitary Method here to get the desired value.
So, Number of hours taken by 1 student = 5/3 = 1.6667.
Therefore, Number of hours taken by 5 students = 1.6667×5 = 8.3335
Types of Unitary Method
There are two types of variation that we see while using Unitary Method under coefficient of variation.
Direct Variation
- This is a direct relationship between the value of the given quantity and the value of the required quantity.
- In other words, if the value of one quantity increases, then the value of the other quantity also increases and vice versa. We can also say that one value is directly proportional to the other value.
- For example, with increase in speed of a car, the distance covered also increases and similarly with decrease with the speed of a car, the distance covered decreases.
- This shows Direct Variation between speed, time and distance.
Indirect Variation
- This is an indirect direct relationship between the value of the given quantity and the value of the required quantity.
- In other words, if the value of one quantity increases, then the value of the other quantity decreases and vice versa. We can also say that one value is inversely proportional to the other value.
- For example, with increase in speed of a car, the time taken to cover a distance decreases, whereas with decrease in speed of a car, the time taken to cover the same distance increases.
- This shows Indirect Variation between speed and time.
Steps to use Unitary Method
The steps to use the unitary method are mentioned below.
- Step 1: First we find the value of unit quantity by dividing the given value by the given quantity. Thus we obtain the value of unit quantity.
- Step 2: We then multiply the required quantity with the obtained value. Therefore we get the value of the required quantity.
Example 2: We have been given the cost of buying 10 balls which is Rs 95, and we need to calculate the cost of 7 balls.
Sol: So according to the above mentioned step 1 we first find the value unit quantity i.e, cost of buying one ball = 95/10 = Rs 9.5
Now we can calculate the value of required quantity mentioned in step 2 by multiplying the cost of 1 ball with the obtained value, i.e., 9.5 x 7 = Rs 68.5
Thus we get the cost of 7 balls using unitary method which is Rs 68.5
 |
Download the notes
Overview: Unitary Method
|
Download as PDF |
Unitary Method in Ratio and Proportion
The Unitary Method is also used to find the ratio of one quantity with respect to another quantity. The concepts of ratio-proportion and unitary method are very much inter-related. The sums of ratio and proportion exercises are based on fractions. A fraction is represented as a:b. The terms a and b can be any two integers.
Example 3: The Income of Harish is Rs 20000 per month, and that of Shalini is Rs 191520 per annum. If the monthly expenditure of each of them is Rs 9000 per month, find the ratio of their savings.
Sol:
- Savings of Harish per month = 20000-9000 = 11000.
- Income of Shalini per month = 191520/12 = 15960
- Savings of Shalini per month = 15960-9000 = 6960
- Therefore, ratio of saving of Harish with respect to savings to Shalini = 11000/6960 = 1.58046
Uses of Unitary Method
Unitary Method has vast use in solving various problems in our day-to-day life. The main uses are listed below.
- It is used to calculate the percentage of any quantity.
- We can find the manpower required to complete a given amount of work.
- If the ratio of area and side of a square is given, then we can find the area of that square through the Unitary Method.
- It is used to find the cost of a certain object, if the cost and quantity is provided.
- It also helps us to calculate the speed of a vehicle for a given distance.
Example 4: The cost of 2 notebooks is Rs. 90. Calculate the cost of 10 notebooks.
Sol: We have the given quantity as 2 and the value of these 2 quantities is Rs. 90.
First we find the value of 1 quantity,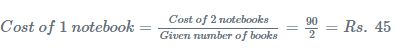
Next we calculate the value of 10 notebooks,
Cost of 10 notebooks = Cost of 1 notebook × Number of 10 books = 45 × 10 = Rs 450
Thus we get the cost of 10 notebooks i.e., Rs. 450
Example 5: Which of the following options is cost effective?
(i) Bottle A costs Rs.55 for 2 Liters
(ii) Bottle B costs Rs.70 for 3 Liters
Sol: We can use the Unitary Method to choose the cost effective option. We can find the cost of 1 liter which will help us to identify the cost effective bottle.
(i) Cost of 1 liter = 55/2 = Rs. 27.5
(ii) Cost of 1 liter = 70/3 = Rs. 23.3
As the cost of 1 liter from bottle B is less than the cost of 1 liter from bottle A.
Thus bottle B is more cost effective.
|
315 videos|182 docs|185 tests
|
















