Overview: Surds | Quantitative Techniques for CLAT PDF Download
| Table of contents |

|
| Surds |

|
| Rules for Surds |

|
| Types of Surds You Need to Focus |

|
| Conclusion |

|
Surds
Surd is a Latin word that means mute or deaf. In the past, Arabian mathematicians referred to rational & irrational numbers as audible & inaudible, respectively. Because surds are formed up of irrational numbers, they were given the Arabic name asamm (deaf, stupid), which was ultimately translated into Latin as surds.
Surds are the square roots of non-trivial numbers. It is impossible to convey accurately in a fraction. In another way, Surd is an irrational root of the whole number. Consider the number √2 ≈1.414213. If we keep it as a surd √2, it will be more correct.
It’s important to keep in mind that an irrational number cannot be stated as a fraction.
Surds are square root values that cannot be easily converted to whole numbers or integers in mathematics.
Rules for Surds
Division of Surds
You can divide surds with various numbers inside the root by combining them into single root & dividing the numbers within the root as long as the indexes of roots are the same.
√a /√b = √a/ b
Example
√14 / √2 = √14/2= √7
Multiplication of Surds
You can multiply surds with various numbers inside the root by combining them into single root & multiplying the numbers within the root as long as the indexes of roots are the same. Factors can also be used to divide a root into many roots.
√a ×√b= √a ×b
Example: √3 ×√5= √3 ×5= √15
Multiplication of Square Root by Itself
You should get the original value if you multiply the square root of an integer by itself.
√a ×√a= √a ×a= √a²=a
Example: √5 ×√5= √5 ×5= √5²=5
Multiplication of Surds containing Brackets
Each term in the 1st bracket should be multiplied by each term in the 2nd bracket in order to multiply brackets containing surds. You can then mix phrases that are similar.
(2+ √3)+(5+√3)=2×5+2√3+5 √3+√3²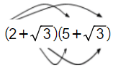
=10+7 √3+√3=1√3+7√3
Multiplication of Number by a Surd
The order of the elements does not matter when multiplying a number by a surd, & the result must be the number followed by surd.
x × √y=√yx=x√y
Example: 3 ×√5=√5×3=3√5
Addition or Subtraction of Surds
The number within the roots should be the same to add or subtract surds. Outside the root, you add and subtract numbers.
a√ x+b√x=(a+b)√x
a √x-b√x=(a-b)√x
Examples: 5 √3+3√3=(5+3)√3=8√3
5 √3-3√3=(5-3)√3=2√3
Types of Surds You Need to Focus
Simple Surds
- A Surd which has a single term is considered as a simple surd. Such as √2, √5, …
Pure Surds
- Surds that are completely irrational are considered as Pure Surds. Such as √3
Similar Surds
- The surds which have the same common Surds factor are termed as similar surds.
Binomial Surds
- A Surd which consists of 2 other surds are termed as Binomial Surds.
Compound Surds
- An expression which is the subtraction or addition of 2 or more Surds are termed as Compound Surds.
Mixed Surds
- Surds which are not complete irrational & Irrational numbers that can be written as a product of a rational and an irrational number.
Conclusion
Surds are expressions which result in an irrational number having infinite decimals when they have a Square Root, Cube Root, or other root. They’ve been left in their original state to better portray them.
The index of roots should be the same to multiply & divide surds with various numbers inside the root.
The number within the roots have to be the same while adding or subtracting surds.
It may be important to simplify surds before subtracting or adding them.
If a square number is a factor in the number within the root of a surd, it can be simplified.
There are following types of surds which are given here;
- Simple Surds
- Pure Surds
- Similar Surds
- Binomial Surds
- Compound Surds
- Mixed Surds.
|
49 videos|179 docs|73 tests
|














