Overview: Statistics | Quantitative Techniques for CLAT PDF Download
| Table of contents |

|
| Understanding Statistical Basics |

|
| Solving Statistics Problems: Concepts and Examples |

|
| Strategies for Tackling Statistics Problems |

|
| Statistical Formula |

|
| Conclusion |

|
Understanding Statistical Basics
Before delving into solving statistics problems, it’s important to grasp the foundational concepts:
- Data: Data refers to information collected from observations, experiments or surveys. It can be in the form of numbers, measurements or categories.
- Variables: Variables are characteristics or attributes that can change. They can be classified as either categorical (qualitative) or numerical (quantitative).
- Mean: The mean, also known as the average, is calculated by summing up all the values and then dividing by the total number of values.
- Median: The median is the middle value in a dataset when arranged in ascending or descending order. It’s a measure of central tendency.
- Mode: The mode is the value that appears most frequently in a dataset.
- Range: The range is the difference between the maximum and minimum values in a dataset.
Solving Statistics Problems: Concepts and Examples
Example 1: Calculating Mean, Median and Mode
(i) Find the mean, median and mode of the following dataset: 12, 15, 18, 22, 22, 25, 30.
Sol:
- Mean: Sum of all values = 12 + 15 + 18 + 22 + 22 + 25 + 30 = 144. Total values = 7. Mean = 144 / 7 ≈ 20.57.
- Median: The middle value is the fourth value (22) since there are seven values. Median = 22.
- Mode: The mode is 22 as it appears most frequently.
Example 2: Calculating Range and Interquartile Range
(i) Calculate the range and interquartile range of the following dataset: 5, 8, 10, 12, 15, 18, 20, 23.
Sol:
- Range: Range = Maximum value – Minimum value = 23 – 5 = 18.
- Interquartile Range (IQR): IQR is the difference between the third quartile (Q3) and the first quartile (Q1). Q1 = 10 and Q3 = 20. IQR = 20 – 10 = 10.
Strategies for Tackling Statistics Problems
Solving statistics problems requires careful analysis and application of mathematical techniques. Here are some strategies to approach statistics problems with confidence:
- Data Organisation: Begin by organising the given data in ascending or descending order. This will help you visualise the data distribution.
- Central Tendency Measures: Understand how to calculate mean, median and mode. Recognise which measure is appropriate for different types of data distributions.
- Range and Spread: Learn to calculate the range and interquartile range. These measures indicate the spread of data values.
- Visualisation: Use graphs and charts like histograms, bar graphs and pie charts to visualise data patterns and relationships.
- Practice Interpretation: Practice interpreting statistical results in the context of real-world situations. This skill is essential for understanding the implications of data analysis.
Statistical Formula
What is statistics?
- Statistics is the study of the collection, analysis, interpretation, presentation, and organization of the large data. The statistical theory defines a statistic as a function of the sample data where the function itself is independent of the sample’s distribution.
- Therefore, Statistics is associated with collecting, classifying, arranging and presenting the numerical data related in some context. It also allows us to interpret many results from it and forecast many possibilities for further applications. Using statistics, we can find various measures of central tendencies and the deviation of different values from the center.
The formula in statistics:
For almost all statistical computations, the basic concepts of mean, median, mode, variance, and standard deviation are the stepping stones.
(i) Mean or Average: Mean in theory is defined as the sum of all the elements of a set divided by the number of elements. We can get a fairly good idea about the whole set of data by calculating its mean. Thus the formula for mean is: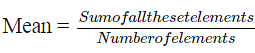
The importance of mean lies in its ability to represent the whole dataset with a single value.
(ii) Median: Median is the middle value of a dataset. So, if a set consists of an odd number of values, then the middle value will be the median of the set. On the other hand, if the set consists of an even number of sets, then the median will be the average of the two middle values.
Thus, the median may be used to separate a set of data into two parts. To find the median of a set, we need to arrange the elements of the set in increasing order. Then find the middle value.
(iii) Mode: The mode in a dataset is the value that is most frequent in the dataset. The mode also summarizes the gdataset with single information.
(iv) Variance: We may want to measure the deviation of a set of data from their mean value. The variance of the particular dataset will always be positive. Variance is used in the calculation of Standard Deviation, which is a very important concept of statistics.
(v) Standard Deviation: The standard deviation is defined as the square rooting of the variance of the data.
Conclusion
Statistics is not just a collection of numbers; it’s a powerful tool for extracting valuable insights from data. By mastering the basics of data analysis, central tendency measures and data spread, you can confidently tackle statistics problems in the CLAT’s Quantitative Aptitude section. Remember to organise data, choose appropriate measures, understand ranges, visualise data and practice interpretation. As you prepare for the CLAT, a solid understanding of statistics will not only enhance your mathematical skills but also equip you with valuable analytical abilities for a wide range of scenarios.
|
57 videos|108 docs|73 tests
|

|
Explore Courses for CLAT exam
|

|
















