NCERT Solutions Class 11 Maths Chapter 10 - Conic Sections
Q1: Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for y2 = 12x
Ans: The given equation is y2 = 12x.
Here, the coefficient of x is positive. Hence, the parabola opens towards the right.
On comparing this equation with y2 = 4ax, we obtain
4a = 12 ⇒ a = 3
∴ Coordinates of the focus = (a, 0) = (3, 0)
Since the given equation involves y2, the axis of the parabola is the x-axis.
Equation of direcctrix, x = –a i.e., x = – 3 i.e., x + 3 = 0
Length of latus rectum = 4a = 4 × 3 = 12
Q2: Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for x2 = 6y
Ans: The given equation is x2 = 6y.
Here, the coefficient of y is positive. Hence, the parabola opens upwards.
On comparing this equation with x2 = 4ay, we obtain
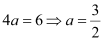
∴ Coordinates of the focus = (0, a) = 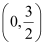
Since the given equation involves x2, the axis of the parabola is the y-axis.
Equation of directrix, 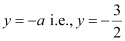
Length of latus rectum = 4a = 6
Q3: Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for y2 = – 8x
Ans: The given equation is y2 = –8x.
Here, the coefficient of x is negative. Hence, the parabola opens towards the left.
On comparing this equation with y2 = –4ax, we obtain
–4a = –8 ⇒ a = 2
∴ Coordinates of the focus = (–a, 0) = (–2, 0)
Since the given equation involves y2, the axis of the parabola is the x-axis.
Equation of directrix, x = a i.e., x = 2
Length of latus rectum = 4a = 8
Q4: Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for x2 = – 16y
Ans: The given equation is x2 = –16y.
Here, the coefficient of y is negative. Hence, the parabola opens downwards.
On comparing this equation with x2 = – 4ay, we obtain
–4a = –16 ⇒ a = 4
∴ Coordinates of the focus = (0, –a) = (0, –4)
Since the given equation involves x2, the axis of the parabola is the y-axis.
Equation of directrix, y = a i.e., y = 4
Length of latus rectum = 4a = 16
Q5: Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for y2 = 10x
Ans: The given equation is y2 = 10x.
Here, the coefficient of x is positive. Hence, the parabola opens towards the right.
On comparing this equation with y2 = 4ax, we obtain
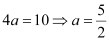
∴ Coordinates of the focus = (a, 0) 
Since the given equation involves y2, the axis of the parabola is the x-axis.
Equation of directrix,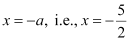
Length of latus rectum = 4a = 10
Q6: Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for x2 = –9y
Ans: The given equation is x2 = –9y.
Here, the coefficient of y is negative. Hence, the parabola opens downwards.
On comparing this equation with x2 = –4ay, we obtain
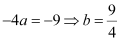
∴ Coordinates of the focus =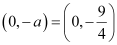
Since the given equation involves x2, the axis of the parabola is the y-axis.
Equation of directrix,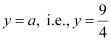
Length of latus rectum = 4a = 9
Q7: Find the equation of the parabola that satisfies the following conditions: Focus (6, 0); directrix x = –6
Ans: Focus (6, 0); directrix, x = –6
Since the focus lies on the x-axis, the x-axis is the axis of the parabola.
Therefore, the equation of the parabola is either of the form y2 = 4ax or
y2 = – 4ax.
It is also seen that the directrix, x = –6 is to the left of the y-axis, while the focus (6, 0) is to the right of the y-axis. Hence, the parabola is of the form y2 = 4ax.
Here, a = 6
Thus, the equation of the parabola is y2 = 24x.
Q8: Find the equation of the parabola that satisfies the following conditions: Focus (0, –3); directrix y = 3
Ans: Focus = (0, –3); directrix y = 3
Since the focus lies on the y-axis, the y-axis is the axis of the parabola.
Therefore, the equation of the parabola is either of the form x2 = 4ay or
x2 = – 4ay.
It is also seen that the directrix, y = 3 is above the x-axis, while the focus
(0, –3) is below the x-axis. Hence, the parabola is of the form x2 = –4ay.
Here, a = 3
Thus, the equation of the parabola is x2 = –12y.
Q9: Find the equation of the parabola that satisfies the following conditions: Vertex (0, 0); focus (3, 0)
Ans: Vertex (0, 0); focus (3, 0)
Since the vertex of the parabola is (0, 0) and the focus lies on the positive x-axis, x-axis is the axis of the parabola, while the equation of the parabola is of the form y2 = 4ax.
Since the focus is (3, 0), a = 3.
Thus, the equation of the parabola is y2 = 4 × 3 × x, i.e., y2 = 12x
Q10: Find the equation of the parabola that satisfies the following conditions: Vertex (0, 0) focus (–2, 0)
Ans: Vertex (0, 0) focus (–2, 0)
Since the vertex of the parabola is (0, 0) and the focus lies on the negative x-axis, x-axis is the axis of the parabola, while the equation of the parabola is of the form y2 = –4ax.
Since the focus is (–2, 0), a = 2.
Thus, the equation of the parabola is y2 = –4(2)x, i.e., y2 = –8x
Q11: Find the equation of the parabola that satisfies the following conditions: Vertex (0, 0) passing through (2, 3) and axis is along x-axis.
Ans: Since the vertex is (0, 0) and the axis of the parabola is the x-axis, the equation of the parabola is either of the form y2 = 4ax or y2 = –4ax.
The parabola passes through point (2, 3), which lies in the first quadrant.
Therefore, the equation of the parabola is of the form y2 = 4ax, while point
(2, 3) must satisfy the equation y2 = 4ax.
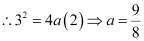
Thus, the equation of the parabola is
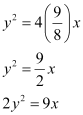
Q12: Find the equation of the parabola that satisfies the following conditions: Vertex (0, 0), passing through (5, 2) and symmetric with respect to y-axis
Ans: Since the vertex is (0, 0) and the parabola is symmetric about the y-axis, the equation of the parabola is either of the form x2 = 4ay or x2 = –4ay.
The parabola passes through point (5, 2), which lies in the first quadrant.
Therefore, the equation of the parabola is of the form x2 = 4ay, while point
(5, 2) must satisfy the equation x2 = 4ay.
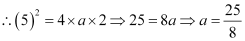
Thus, the equation of the parabola is
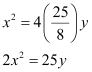
|
172 videos|476 docs|154 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 10 - Conic Sections
| 1. What are conic sections? |  |
| 2. How are conic sections useful in real life? |  |
| 3. What is the general equation of a conic section? |  |
| 4. What is the difference between an ellipse and a hyperbola? |  |
| 5. How can conic sections be used to solve real-world problems? |  |





















