Syllabus: Mathematics for Class 10 | Mathematics (Maths) Class 10 PDF Download
The revised Class 10 Mathematics syllabus aligns with the National Curriculum Framework 2005, focusing on real-life applications and problem-solving. It aims to strengthen algebraic and trigonometric skills, foster logical thinking, and promote awareness of societal issues. Teaching methods include hands-on activities, models, and experiments. Students are encouraged to appreciate mathematics as a problem-solving tool, develop technological skills, and participate in competitions. Before exams, it's crucial to understand the syllabus thoroughly for effective practice.

CBSE Class 10 Mathematics Syllabus 2025-2026
The topic-wise marks distribution and weightage of CBSE Class 10 Maths are given below: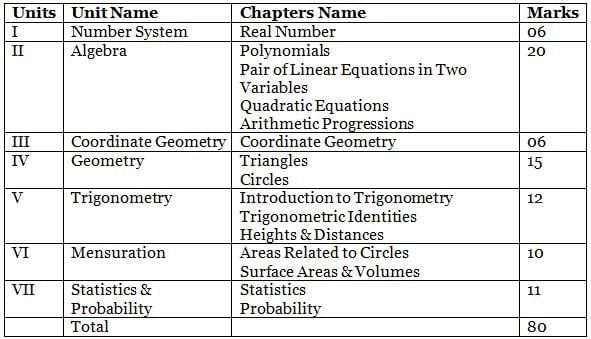
Unit I: Number Systems
- Fundamental Theorem of Arithmetic - statements after reviewing work done earlier, and after illustrating and motivating through examples
- Proofs of irrationality of √2, √3, √5.
Competencies
- Develops understanding of numbers, including the set of real numbers and its properties.
- Extends the understanding of powers (rational powers) and exponents.
- Applies the Fundamental Theorem of Arithmetic to solve problems related to real-life contexts.
Explanation
- Describes the Fundamental Theorem of Arithmetic with examples
- Prove algebraically the Irrationality of numbers like √2, √3 √5, 3 + 2√5 etc.
Unit II: Algebra
- Zeros of a polynomial.
- Relationship between zeros and coefficients of quadratic polynomials.
Competencies
- Develops a relationship between algebraic and graphical methods of finding the zeroes of a polynomial
Explanation
- Find the zeros of polynomial graphically and algebraically and verifying the relation between zeros and coefficients of quadratic polynomials.
2. Pair of Linear Equations in Two Variables
- Pair of linear equations in two variables and graphical method of their solution, consistency/inconsistency.
- Algebraic conditions for number of solutions.
- Solution of a pair of linear equations in two variables algebraically - by substitution, by elimination. Simple situational problems.
Competencies
- Describes plotting a pair of linear equations and graphically finding the solution.
- Models and solves contextualised problems using equations (e.g., simultaneous linear equations in two variables)
Explanation
- Find the solution of a pair of linear equations in two variables graphically and algebraically (substitution and elimination method)
- Standard form of a quadratic equation ax2 + bx + c = 0, (a ≠ 0).
- Solutions of quadratic equations (only real roots) by factorization, and by using the quadratic formula. Relationship between discriminant and nature of roots.
- Situational problems based on quadratic equations related to day-to-day activities are to be incorporated.
Competencies
- Demonstrates strategies for finding roots and determining the nature of roots of a quadratic equation.
Explanation
- Solves quadratic equations using factorization and the quadratic formula
- Determines the nature of roots using discriminant · Formulates and solves problems based on real life context
- Motivation for studying Arithmetic Progression.
- Derivation of the nth term and sum of the first n terms of A.P. and their application in solving daily life problems.
Competencies
- Develops strategies to apply the concept of A.P. to daily life situations.
Explanation
- Applies concepts of AP to find the nth term and sum of n terms.
- Application of AP in real life problems
Unit III: Coordinate Geometry
- Review: Concepts of coordinate geometry, graphs of linear equations. Distance formula.
Section formula (internal division).
Competencies
- Derives formulae to establish relations for geometrical shapes in the context of a coordinate plane, such as, finding the distance between two given points, to determine the coordinates of a point between any two given points.
Explanation
- Solves problems using distance formula and section formula
Unit IV: Geometry
- Definitions, examples, counter examples of similar triangles.
1. (Prove) If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
2. (Motivate) If a line divides two sides of a triangle in the same ratio, the line is parallel to the third side.
3. (Motivate) If in two triangles, the corresponding angles are equal, their corresponding sides are proportional and the triangles are similar.
4. (Motivate) If the corresponding sides of two triangles are proportional, their corresponding angles are equal and the two triangles are similar.
5. (Motivate) If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are proportional, the two triangles are similar.
Competencies
- Works out ways to differentiate between congruent and similar figures.
- Establishes properties for the similarity of two triangles logically using different geometric criteria established earlier, such as, Basic Proportionality Theorem, etc.
Explanation
- Prove the Basic Proportionality theorem and apply the theorem and its converse in solving questions
- Prove the similarity of triangles using different similarity criteria
- Tangent to a circle at the point of contact
1. (Prove) The tangent at any point of a circle is perpendicular to the radius through the point of contact.
2. (Prove) The lengths of tangents drawn from an external point to a circle are equal.
Competencies
- Derives proofs of theorems related to the tangents of circles.
Explanation
- Prove the theorems based on the tangent to a circle.
- Applies the concept of tangents of circle to solve various problems.
Unit V: Trigonometry
1. Introduction to Trigonometry
- Trigonometric ratios of an acute angle of a right-angled triangle. Proof of their existence (well-defined).
- Motivate the ratios that are defined at 0º and 90º. Values of the trigonometric ratios of 30º, 45º and 60º.
- Relationships between the ratios.
Competencies
- Understands the definitions of the basic trigonometric functions (including the introduction of the sine and cosine functions).
Explanation
- Evaluates trigonometric ratios
- Describes trigonometric ratios of standard angles and solving related expressions
- Proof and applications of the identity sin2A + cos2A = 1.
- Only simple identities are to be given.
Competencies
- Uses Trigonometric identities to solve problems.
Explanation
- Proves trigonometric identities using sin2A + cos2A = 1 and other identities
- Simple problems on heights and distances.
- Problems should not involve more than two right triangles.
- Angles of elevation/depression should be only 30°, 45°, and 60°.
Competencies
- Applies Trigonometric ratios in solving problems in daily life contexts, like finding the heights of different structures or the distance from them.
Explanation
- Find heights and distances in real-life word problems using trigonometric ratios
Unit VI: Mensuration
- Area of sectors and segments of a circle.
- Problems based on areas and perimeter or circumference of the above-mentioned plane figures. (In calculating area of a segment of a circle, problems should be restricted to central angles of 60°, 90°, and 120° only)
Competencies
- Derives and uses formulae to calculate areas of plane figures.
Explanation
- Visualises and evaluates areas of sector and segment of a circle
- Surface areas and volumes of combinations of any two of the following: cubes, cuboids, spheres, hemispheres, and right circular cylinders/cones.
Competencies
- Visualises and uses mathematical thinking to discover formulae to calculate surface areas and volumes of solid objects (cubes, cuboids, spheres, hemispheres, right circular cylinders/cones, and their combinations).
Explanation
- Evaluates the surface areas and volumes of combinations of solids by visualisation
Unit VII: Statistics And Probability
- Mean, median and mode of grouped data (bimodal situation to be avoided).
Competencies
- Calculates mean, median, and mode for different sets of data related to real-life contexts.
Explanation
- Computes the mean of a grouped frequency distribution using the direct, assumed mean, and step deviation method.
- Computes the median and mode of a grouped frequency distribution using the algebraic method.
- Classical definition of probability.
- Simple problems on finding the probability of an event.
Competencies
- Applies concepts from probability to solve problems on the likelihood of everyday events.
Explanation
- Determines the probabilities in simple real-life problems
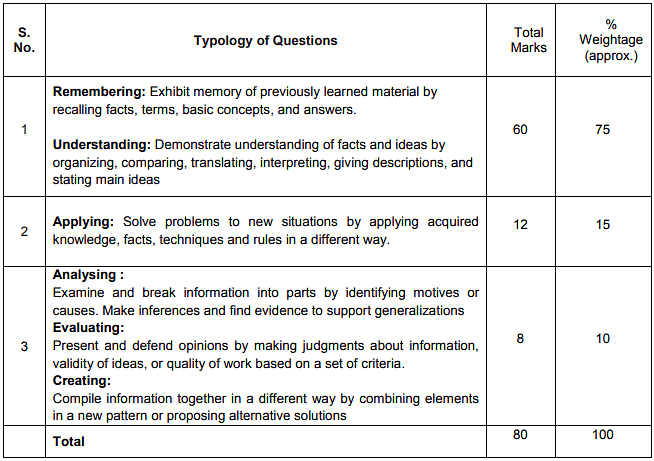
Question Paper Design: Standard
- Time: 3 hours
- Max. marks: 80


Question Paper Design: Basic
- Time: 3 hours
- Max. marks: 80

Prescribed Books:
1. Mathematics - Textbook for class IX - NCERT Publication
2. Mathematics - Textbook for class X - NCERT Publication
3. Guidelines for Mathematics Laboratory in Schools, Class IX - CBSE Publication
4. Guidelines for Mathematics Laboratory in Schools, Class X - CBSE Publication
5. Laboratory Manual - Mathematics, secondary stage - NCERT Publication
6. Mathematics Exemplar Problems for class IX, NCERT publication.
7. Mathematics Exemplar Problems for class X, NCERT publication.
If you want guidance on how to prepare for mathematics, do check out the document How to Prepare for Class 10 Mathematics?
|
127 videos|584 docs|79 tests
|
FAQs on Syllabus: Mathematics for Class 10 - Mathematics (Maths) Class 10
| 1. What are the main topics included in the CBSE Class 10 Mathematics syllabus? |  |
| 2. How is the Question Paper designed for Class 10 Mathematics? |  |
| 3. What is the difference between the Standard and Basic question papers in Class 10 Mathematics? |  |
| 4. How can students effectively prepare for the Class 10 Mathematics exam? |  |
| 5. What resources can students use to study for the CBSE Class 10 Mathematics exam? |  |






















