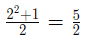Tips and Tricks : Number Series | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
Introduction
- Number series questions test a candidate’s ability to identify patterns, apply mathematical reasoning, and solve problems efficiently under time constraints.
- This document provides tips, tricks, and shortcuts for solving various types of number series, including arithmetic, geometric, perfect square, perfect cube, ratio, and mixed series.

Identifying Patterns
To solve number series questions efficiently, follow these steps:
Check Differences: Calculate the difference between consecutive terms to identify arithmetic or step-up patterns.
Test Ratios: Divide consecutive terms to check for geometric or ratio series.
Look for Squares/Cubes: Verify if terms are perfect squares (1, 4, 9, …) or cubes (1, 8, 27, …).
Examine Prime Numbers: Check if terms follow prime numbers (2, 3, 5, …) or their squares.
Consider Mixed Patterns: Look for alternating operations (e.g., add then multiply) in complex series.
Use Visual Aids: Plot terms on a number line or graph to visualise trends.
Number Series Tips, Tricks and Shortcuts
1. Perfect Square Series
- Comprising a sequence of numbers that are perfect squares arranged in a specific order, the series has one number omitted.
- Our task is to identify the underlying pattern in the series and fill in the blank by determining that missing number.
Example: 100,121,144,__, 196
Sol: This series consists of a perfect square of consecutive numbers 10, 11, 12, 13
Hence 169 will come in the blank.
2. Perfect Cube Series
- It comprises a sequence of numbers arranged in a specific order, where each number is the cube of a given value, and the sequence involves continuously adding these cubic values.
Example: 9,64, 125, __, 343
Sol: This series consists of a series of numbers with perfect cubes that is (3 x 3 x 3), (4 x 4 x 4), (5 x 5 x 5), (6 x 6 x 6), (7 x 7 x 7)
Hence, 216 will be coming in the blank, as the series is following a trend of cubes of numbers in sequential order.
3. Ratio Series
- This series is composed of numbers organised sequentially, adhering to a specific trend, whether it be an increase or decrease.
- Our objective is to identify this trend (which may involve *, /, +, or -) for each number in the series with respect to a constant value.
- This entails determining the proportional difference between consecutive numbers in the series.
Example: 3, 6, 9, 12, __, 18, 21
Sol: Here the series is following an increasing trend in which three is added to each number of the series.
3
6 (3+3)
9 (6+3)
12 (9+3)
15 (12+3)
18 (15+3)
21 (18+3)
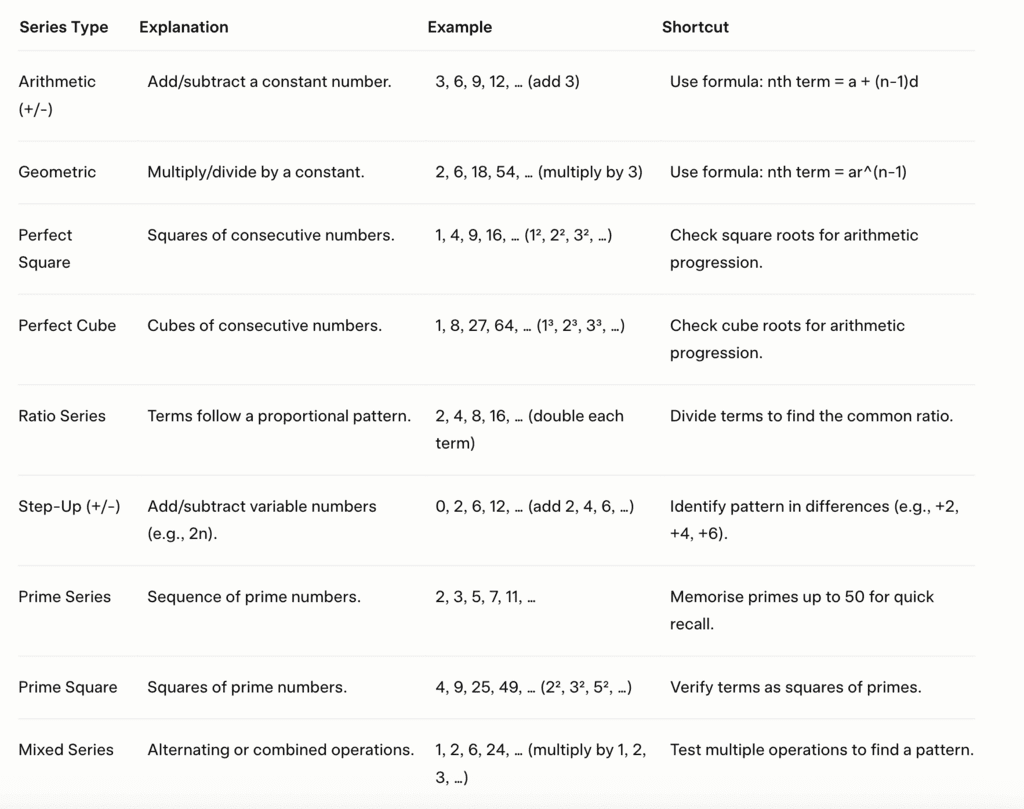
4. Arithmetic series
- In sequences of this nature, each number is derived by either adding or subtracting a constant number from each term.
- The formula for an arithmetic sequence (AS) is given by {a, a+d, a+2d, ...}, where:
a represents the first term of the series,
d is the common difference between consecutive terms.
Example: 3, 6, 9 , 12
Sol: Here a = 3(first term of the series)
d = 3
Hence we get:
3 + 3 = 6
6 + 3 = 9
9 + 3 = 12
12 + 3 = 15
5. Geometric series
In sequences of this type, each number is obtained by multiplying or dividing each term by a constant number.
The formula for a geometric sequence (GS) is represented as {a, ar, ar2, ar3, ...}, where:
- a denotes the first term of the series,
- r is the factor or difference between terms, commonly known as the common ratio.
Example: 1, 2, 4, 8, 16, 32
Sol: Here a = 1 (first term of the series)
r = 2 (a standard number that is multiplied with the consecutive number of the series)
Hence, we get:
1
1 x 2
1 x 22
1 x 23, ….)
6. Mixed series
- In these series, when computing the difference, two steps may be required to obtain the next consecutive number in the series.
- Therefore, we must adhere to the same pattern to determine subsequent numbers in the series.
Example: 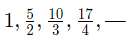
(a) 26/5
(b) 24/5
(c) 21/5
(d) 5
Sol: Here we’ve to observe the trend that this series is following, as each term is divided by a specific number, i.e., 1 then 2 then3 then 4 and so on. Hence, we can make out that the denominator must be 5.
Now comes the numerator, where the 1’st number is 1.
Then comes 5, now how can we get 5 from the term number 2. It can come by
Next comes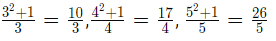
Solved Examples
Q1: 1, 9, 25, 49, ?
A: 81
B: 64
C: 100
D: 36
Ans: A
Sol:
Here the series is squares of odd numbers i.e., 1², 3², 5², 7² and so on.
∴ The next term will be 9² = 81.
Hence, option (a).
Q2: 0, 1, 1, 2, 3, 5, 8, ?
A: 16
B: 13
C: 25
D: 20
Ans: B
Sol:
Here each term is the sum of preceding two terms.
∴ The next term will be = 5 + 8 = 13.
Hence, option (b).
Q3: 17, 29, 53, 89, 137, ?
A: 197
B: 209
C: 185
D: 180
Ans: A
Sol:
Here each subsequent term increases by consecutive multiples of 12 i.e., +12, +24, +36, +48 and so on.
∴ The next term will be = 137 + 60 = 197.
Hence, option (a).
Q4: 13, 26, 23, 46, 43, 86, ?
A: 242
B: 269
C: 253
D: 287
Ans: A
Sol:
Here the pattern is × 2, - 3, × 2, - 3, × 2, - 3 and so on.
∴ The next term will be = 86 – 3 = 83.
Hence, option (a).
Q5: 14, 31, 65, 133, ?
A: 242
B: 269
C: 253
D: 287
Ans: B
Sol:
Here each term of the series is the preceding number multiplied by 2 and then increased by 3 i.e.,
31 = 2 × 14 + 3,
65 = 2 × 31 + 3,
133 = 2 × 65 + 3 and so on.
∴ The next term will be = 133 × 2 + 3 = 269.
Hence, option (b).
Q6: 6, 18, 55, 167, 504, ?
A: 1581
B: 1585
C: 1556
D: 1516
Ans: D
Sol:
Here the series is: 18 = 6 × 3 + 0, 55 = 18 × 3 + 1, 167 = 55 × 3 + 2, 504 = 167 × 3 + 3… and so on. ∴ The next term will be = 504 × 3 + 4 = 1516. Hence, option (d).
Q7: 1200, 240, 60, 20, ?
A: 14
B: 10
C: 12
D: 2
Ans: B
Sol:
Here the series is:
1200 ÷ 5 = 240,
240 ÷ 4 = 60,
60 ÷ 3 = 20, and so on.
∴ The next term will be = 20 ÷ 2 = 10.
Hence, option (b).
Common Mistakes to Avoid
Misidentifying Series Type: Assuming an arithmetic series when ratios indicate a geometric series (e.g., 2, 4, 8 is geometric, not arithmetic).
Ignoring Mixed Patterns: Overlooking alternating operations in mixed series (e.g., 1, 2, 6, 24 requires multiplying by increasing numbers).
Calculation Errors: Miscomputing differences or ratios due to haste (e.g., 3, 6, 9 has a difference of 3, not 2).
Forgetting Formulas: Not applying arithmetic or geometric formulas for nth term or sum, leading to manual errors.
Overcomplicating Simple Series: Treating a perfect square series as a complex pattern (e.g., 1, 4, 9 is simply n²).
|
77 videos|180 docs|96 tests
|
FAQs on Tips and Tricks : Number Series - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What are some tips and tricks for solving number series involving perfect squares? |  |
| 2. How can I solve number series involving perfect cubes? |  |
| 3. What shortcuts can I use to solve ratio series in number sequences? |  |
| 4. How can I approach arithmetic series in number sequences? |  |
| 5. What tips and tricks can I use for solving geometric series in number sequences? |  |