Types of Functions | Mathematics (Maths) Class 12 - JEE PDF Download

Introduction

Functions are defined as the relations which give a particular output for a particular input value. A function has a domain and codomain (range). f(x) usually denotes a function where x is the input of the function. In general, a function is written as y = f(x).

What is a Function?

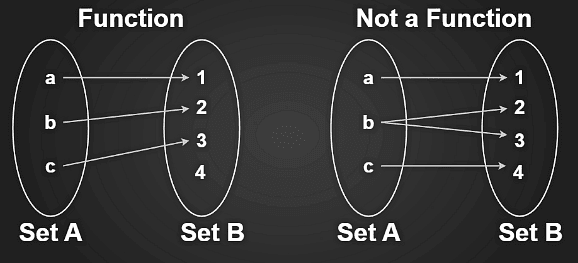
• A function is a relation between two sets set A and set B. Such that every element of set A has an image in set B and no element in set A has more than one image in set B.
• Let A and B be two nonempty sets. A function or mapping f from A to B is written as f: A -> B is a rule by which each element a ∈ A is associated with a unique element b ∈ B
  

Condition for a Function

• A function is a relation in which a particular input gives a particular output i.e. every input value has a particular output and no input value has more than one output. Now, for any two non-empty sets A and B, a function f: A->B denotes that f is a function from A to B, where A is a domain and B is a co-domain.
• For any element, a ∈ A, a unique element, b ∈ B is there such that (a,b) ∈ f.
  The unique element b which is related to a is denoted by f(a) and is read as f of a.

Vertical Line Test

Vertical line test is used to determine whether a curve is a  function or not. If any curve cuts a vertical line at more than one point then the curve is not a function.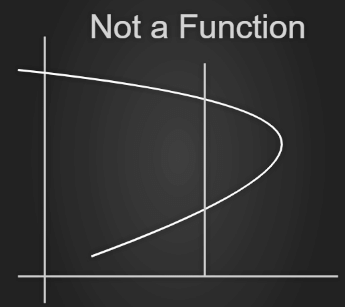

When will Function Not Exist? 

• The condition when the function does not exists is when all the elements of the domain are not mapped with the codomain element if any one of the elements will be left to be mapped with the codomain then the function will not exist.
  
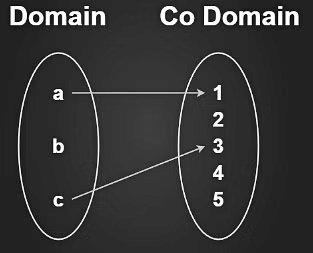
• From the above example, we can see that all the elements of the domain are not mapped b element is left to be mapped so in this condition our function does not exist for this particular domain.

Function in Algebra

Function in algebra is an equation that gives a relation between a particular value of input say x with the particular value of output say y. A function is written as,

y = f(x)

where

• x is the independent variable,
• y is the dependent variable

Example: Some functions in algebra are:

• y = x+ 2,
• y = x² + x + 1, etc

Domain, Codomain, and Range of a Function

The elements of set X are called the domain of f and the elements of set Y are called the codomain of f. The images of the elements of set X are called the range of function, which is always a subset of Y. The image given below demonstrates the domain, codomain, and range of the function.

The image demonstrates the domain, co-domain, and range of the function. Remember the element which is mapped only will be counted in the range as shown in the image. The domain, codomain, and range of the above function are

• Domain = {a, b, c}
• Codomain = {1, 2, 3, 4, 5}
• Range = {1, 2, 3}

Types of Functions in Maths

• An example of a simple function is f(x) = x³. In this function, f(x) takes the value of “x” and then cubes it to find the value of the function. For example, if the value of x is taken to be 2, then the function gives 8 as output i.e. f(2) = 8.
• Some other examples of functions are: f(x) = cos x, f(x) = 5x² + 9, f(x) = 1/x³, etc.

There are several types of functions in maths. Some of the important types are:

• One to One (Injective) function
• Many to One function
• Onto (Surjective) Function
• Into Function

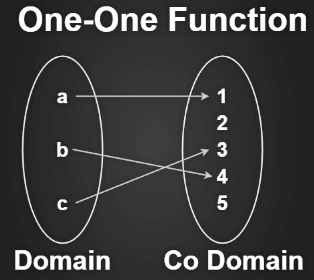
One to One (Injective) function

A function f: X -> Y is said to be a one-to-one function if the images of distinct elements of X under f are distinct. Thus, f is one to one if f(x₁) = f(x₂)

• Property: A function f: A -> B is one-to-one if f(x₁) = f(x₂) implies x₁ = x₂, i.e, an image of a distinct element of A under f mapping (function) is distinct.
• Condition to be One-to-One function: Every element of the domain has a single image with a codomain after mapping.
  

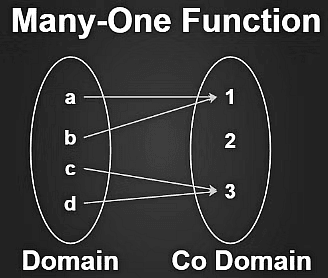
Many to One function

If the function is not one to one function then it should be many to one function means every element of the domain has more than one image at codomain after mapping.

• Property: One or more elements having the same image in the codomain
• Condition to be Many to One function: One or more than one element in the domain having a single image in the codomain.
  

Onto (Surjective) Function

A function f: X -> Y is said to be an onto function if every element of Y is an image of some element of set X under f, i.e for every y ∈ Y there exists an element x in X such that f(x) = y.

Properties:

• The range of functions should be equal to the codomain.
• Every element of B is the image of some element of A.

Condition to be Onto function: The range of function should be equal to the codomain.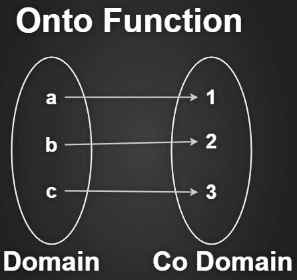

As we see in the above two images, the range is equal to the codomain means that every element of the codomain is mapped with the element of the domain, as we know that elements that are mapped in the codomain are known as the range. So these are examples of the Onto function.

Into Function

• A function f: X -> Y is said to be an into a function if there exists at least one element or more than one element in Y, which does not have any pre-images in X, which simply means that every element of the codomain are not mapped with elements of the domain.
  
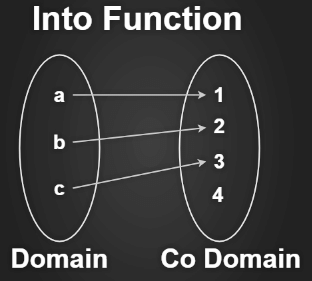
• From the above image, we can clearly see that every element of the codomain is not mapped with elements of the domain means the 10th element of the codomain is left unmapped. So this type of function is known as Into function.

Properties: 

• The Range of function is the proper subset of B
• The Range of functions should not equal B, where B is the codomain.

Solved Examples on Function

Example 1: Check whether the function f(x) = 2x + 3, is one-to-one or not if Domain = {1, 2, 1/2} and Codomain = {5, 7, 4}
Solution:
Putting 1, 2, 1/2 in place of x in f(x) = 2x + 3, we get
f(1) = 5,
f(2) = 7,
f(1/2) = 4
As, for every value of x we get a unique f(x) thus, we can conclude that our function f(x) is One to One.

Example 2: Check whether the function is one-to-one or not: f(x) = 3x – 2
Solution:
To check whether a function is one to one or not, we have to check that elements of the domain have only a single pre-image in codomain or not. For checking, we can write the function as,
f(x₁) = f(x₂)
3x₁ – 2 = 3x₂ – 2
3x₁ = 3x₂ 
x₁ = x₂ 
Since both x₁ =  x₂ which means that elements of the domain having a single pre-image in its codomain. Hence the function f(x) = 3x – 2 is one to one function.

Example 3: Check whether the function is one-to-one or not: f(x) = x² + 3.
Solution: 
To check whether the function is One to One or not, we will follow the same procedure. Now let’s check, we can write the function as,
f(x₁) = f(x₂)
(x₁)² + 3 = (x₂)² + 3
(x₁)² = (x₂)² 
Since (x₁)² = (x₂)² is not always true.
Hence the function f(x) = x² + 3 is not one to one function.

Example 4: If N: -> N, f(x) = 2x + 1 then check whether the function is injective or not.
Solution:
In question N -> N, where N belongs to Natural Number, which means that the domain and codomain of the function is a natural number. For checking whether the function is injective or not, we can write the functions as,
Let, f(x₁) = f(x₂)
2x₁ + 1= 2x₂ + 1
2x₁ = 2x₂ 
x₁ = x₂
Since x₁ = x₂, means all elements of the domain are mapped with a single element of the codomain. Hence function f(x) = 2x + 1 is Injective (One to One).

Example 5: f(x) = x², check whether the function is Many to One or not.
Solution:
Domain = {1, -1, 2, -2}, let’s put the elements of the domain in the function
f(1) = 1² = 1
f(-1) = (-1)² = 1
f(2) = (2)² = 4
f(-2) = (-2)² = 4
Thus, we can see that more than one element of the domain have similar image after mapping. So this is Many to One function.

Example 6: If f(x) = 2x + 1 is defined on R:-> R. Then check whether the following function is Onto or not
Solution: 
For checking the function is Onto or not, Let’s first put the function f(x) equal to y
f(x) = y
y = 2x + 1
y – 1 = 2x
x = (y – 1) / 2
Now put the value of x in the function f(x), we get,
f((y – 1) / 2) = 2 × [(y – 1) / 2] +1
Taking LCM 2, we get
= [2(y – 1) + 2] / 2
= (2y – 2 + 2) / 2
= y
Since we get back y after putting the value of x in the function. Hence the given function f(x) = 2x + 1 is Onto function.

Example 7: If f:N -> N is defined by f(x) = 3x + 1. Then prove that function f(x) is Surjective.
Solution:
To prove that the function is Surjective or not, firstly we put the function equal to y. Then find out the value of x and then put that value in the function. So let’s start solving it.
Let f(x) = y
3x + 1 = y
3x = y – 1
x = (y – 1) / 3
Now put the value of x in the function f(x), we get
f((y – 1) / 3) = {3 (y – 1) / 3} + 1
= y – 1 + 1
= y
Since we get back y after putting the value of x in the function. Hence the given function f(x) = (3x + 1) is Onto function.

Example 8: If A = R – {3} and B = R – {1}. Consider the function f: A -> B defined by f(x) = (x – 2)/(x – 3), for all x ∈ A. Then show that the function f is bijective.
Solution:
To show the function is bijective we have to prove the given function both One to One and Onto.
Let’s first check for One to One:
Let x₁, x₂ ∈  A such that f(x₁) = f(x₂)
Then, (x₁ – 2) / (x₁ – 3) = (x₂ – 2) / (x₂ – 3)
(x₁ – 2) ( x₂ – 3) = (x₂ – 2) (x₁ – 3)
x₁ . x₂ – 3x₁ – 2x₁ + 6 = x₁ . x₂ – 3x₂ -2x₁ + 6
-3x₁ – 2x₂ = -3x₂ – 2x₁
-3( x₁ – x₂) + 2( x₁ – x₂) = 0
-( x₁ – x₂) = 0
x1 – x₂  = 0
⇒ x₁ = x₂
Thus, f(x₁) = f(x₂) ⇒ x₁ = x₂, ∀ x1, x2  ∈ A
So, the function is a One to One
Now let us check for Onto:
Let y ∈ B = R – {1} be any arbitrary element.
Then, f(x) = y
⇒ (x – 2) / (x – 3) = y
⇒ x – 2 = xy – 3y
⇒ x – xy = 2 – 3y
⇒ x(1 – y) = 2 – 3y
⇒ x =  (2 – 3y) / (1 – y) or x = (3y – 2) / (y – 1)
Now put the value of x in the function f(x)
f((3y – 2) / (y – 1)) = { (3y – 2) / (y – 1) } – 2 / { (3y – 2) / (y – 1) – 3 }
= (3y – 2 – 2y + 2) / (3y – 2 – 3y + 3)
= y
Hence f(x) is Onto function. Since we proved both One to One and Onto this implies that the function is Bijective.

Example 9: A = {1, 2, 3, 4}, B = {a, b, c, d} then the function is defined as f = {(1, a), (2, b), (3, c), (4, d)}. Check whether the function is One to One Onto or not.
Solution: 
To check whether the function is One to One Onto or not. We have to check for both one by one.
Let’s check for One to One:

• As we know the condition for One to One that all the elements of the domain are having a single image in the codomain. As we see in the mapping that all the elements of set A are mapped with set B and each having a single image after mapping. 
• So the function is One to One.

Now let’s check for Onto:

• As we know the condition for the function to be Onto is that, Range = Codomain means all the elements of codomain are mapped with domain elements, in this case, codomain will equal to the domain. As we see in the mapping that the condition of the function to be Onto is satisfied. 
• So the function is Onto. 
• Since we had proved that the function is both One to One and Onto. 
• Hence function is One to One Onto (Bijective).

Example 10: A = {1, 2, 3, 4}, B = {a, b, c, d}. The function is defined as f = {(1, a), (2, b), (3, c), (4, c)}. Check whether the function is Many to One Into or not.
Solution:
To check the function is Many to One Into or not. We have to check for both one by one.

Let’s first check for Many to One function:
As we know the condition for Many to One function is that more than one element of domain should have more same image in codomain. From the above mapping we can see that the elements of A {3, 4 } are having same image in B { c }, so the function is Many to One.

Now let’s check for Into function:
As we know the condition for Into function is that the Range of function should be the subset of codomain and also not equal to codomain. Let’s check both the conditions are satisfied or not.

• Range of function = {a, b, c}
• Codomain of function = {a, b, c, d}

Range of function ≠ Codomain of function
As we check that the range of function is not equal to codomain of the function. Hence we can say that the function is Into function. As we prove that the function is Many to One and Into.
Hence the function is Many to One Into.