Formulas: Probability | Quantitative Aptitude for SSC CGL PDF Download
Formula & Definition for Probability
- Probability is a numerical representation indicating the likelihood or possibility of a specific event occurring.
- Probability signifies the degree to which events happen. When events occur, such as throwing a ball or selecting a card from a deck, there is a corresponding probability associated with each event.
- In mathematical terms, probability is defined as the ratio of favorable outcomes to the total number of possible outcomes. The theory of probability encompasses three approaches: the Classical Approach, Relative Frequency Approach, and Subjective Approach.
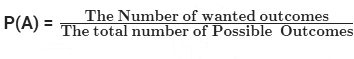

Basic Definition and Formula
- Random Event: If an experiment is repeated numerous times under similar conditions and does not yield the same result each time, but the outcome in a trial is one of several possible outcomes, then such an experiment is termed a random event or a probabilistic event.
- Elementary Event: The elementary event represents the outcome of each occurrence of a random event. Whenever the random event takes place, each corresponding outcome is referred to as an elementary event.
- Sample Space: The sample space denotes the set of all conceivable outcomes of a random event. For instance, when a coin is tossed, the potential outcomes are heads and tails.
- Event: An event is a subset of the sample space associated with a random event.
- Occurrence of an Event: An event linked to a random event is considered to occur if any of the elementary events within it is an actual outcome.
Basic Probability Formulas
- Probability Range – 0 ≤ P(A) ≤ 1
- Rule of Complementary Events – P(AC) + P(A) =1
- Rule of Addition – P(A∪B) = P(A) + P(B) – P(A∩B)
- Disjoint Events – Events A and B are disjoint if P(A∩B) = 0
- Conditional Probability –
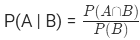
- Bayes Formula –
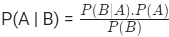
- Independent Events – Events A and B are independent if. P(A∩B) = P(A) ⋅ P(B).
Sample Probability Based Questions
Q1: In a bag, there are 7 red marbles, 5 blue marbles, and 4 green marbles. Two marbles are randomly selected from the bag without replacement. What is the probability that both of them are blue?
Sol:
For the first draw, Probability of selecting a blue marble is 5/16 (5 blue marbles out of 16 total marbles).
After the first marble is drawn, there are 4 blue marbles left out of 15 total marbles.
For the second draw, the probability of selecting a blue marble is 4/15.
To calculate the probability of both marbles being blue => 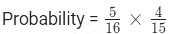
Probability = 20/24 = 1/22
Q2: In a bag, there are 3 green bulbs, 4 orange bulbs, and 5 white bulbs. A bulb is randomly picked from the bag. What is the probability of selecting either a green bulb or a white bulb?
Sol:
Total number of bulbs in the bag is 3 green + 4 orange + 5 white = 12 bulbs
Number of green bulbs is 3, and the number of white bulbs is 5
Probability of selecting either a green or a white bulb, we add the number of green bulbs and the number of white bulbs, and then divide it by the total number of bulbs.
Probability = (Number of green bulbs + Number of white bulbs) / Total number of bulbs
Probability = 8/12
Probability = 2/3
Q3: Joey Tribbiani organized a rack race with two participants. The probability of the first participant winning is 2/7, and the probability of the second participant winning is 3/5. What is the probability that one of them will win?
Sol:
Let’s denote:
P(A) = Probability of the first participant winning = 2/7
P(B) = Probability of the second participant winning = 3/5
The probability of both participants winning simultaneously (a tie) is zero since there can only be one winner. Therefore, the probability that one of them will win is:
P(one of them wins) = P(A) + P(B) – P(A and B)
P(one of them wins) = P(A) + P(B) – 0 (since P(A and B) = 0)
P(one of them wins) = P(A) + P(B)
Substituting the given probabilities: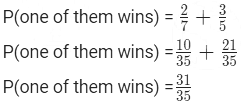
Q4: In a drawer, there are 4 black pens, 3 blue pens, and 5 red pens. A pen is drawn at random from the drawer. What is the probability that it is either black or blue?
Sol:
We have calculate the probability of drawing a black or blue pen from the drawer
The total no. of pens in the drawer is 4 black + 3 blue + 5 red = 12 pens
Probability of drawing a black pen is 4/12
Probability of drawing a blue pen is 3/12 = 1/4
Hence, The probability of drawing either a black or blue pen, we add the individual probabilities:
Probability = 4/12 + 3/12
Probability = 7/12
Q5: Sylvester Stallone brought a box of balloons for a group of students. The box contains 3 balloons of Shape A, 4 balloons of Shape B, and 5 balloons of Shape C. If three balloons are randomly drawn from the box, what is the probability that all three balloons are of different shapes?
Sol:
Total No. of Balloons = 3 Balloons of Shape A +4 Balloons of Shape B + 5 Balloons of Shape C = 12
n(s)= 12C3 = 220
n(e)= 3C1 ∗ 4C1 ∗ 5C1 = 60
P= 60/220 = 3/11
|
342 videos|298 docs|185 tests
|
FAQs on Formulas: Probability - Quantitative Aptitude for SSC CGL
| 1. What is the definition of probability? |  |
| 2. How is probability calculated? |  |
| 3. Can the probability of an event be greater than 1? |  |
| 4. What is the meaning of mutually exclusive events in probability? |  |
| 5. How do you calculate the probability of independent events? |  |
















