Solved Examples: Height & Distance | Quantitative Aptitude for SSC CGL PDF Download
| Table of contents |

|
| Height |

|
| Distance |

|
| Terms |

|
| Solved Examples |

|
Height
The measurement of an object vertically known as Height.
Distance
Distance is the measurement of an object from a particular point in the horizontal direction.
Terms
 |
MCQ: Height & Distance - 1
|
Start Test |
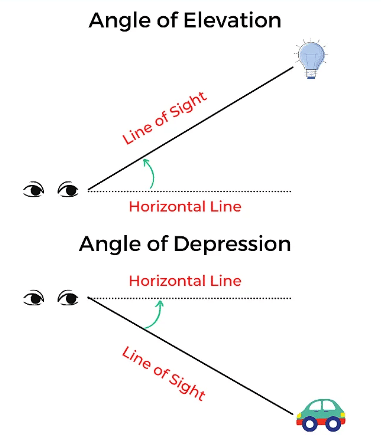
The angle of Elevation
The concept becomes clearer when examining a scenario where an individual stands on the ground, gazing at an object positioned at an elevated point, such as the pinnacle of a building. In this instance, the connecting line from the person's eye to the building's top is termed the "line of sight." The angle formed between the line of sight and the horizontal line is referred to as the "angle of elevation."
The angle of Depression
In a different scenario, when an individual is positioned at an elevated point relative to an object being observed, the line connecting the person's eye to the bottom of the building is termed the "line of sight" as well. The angle formed by this line of sight and the horizontal line is identified as the "angle of depression."
 |
Download the notes
Solved Examples: Height & Distance
|
Download as PDF |
Solved Examples
Example 1: The angles of depression of the top and bottom of a tree, as observed from the top of a building, which is 90mtrs high are 300 and 600. What is the height of the tree?
(a) 60 m
(b) 20 m
(c) 10 m
(d) 50 m
Ans: (a)
Let the tower be AB of height 90mtr
Let the tree be = CD
In the above triangle ABC, tan 600 = AB/AC
AC = 30√3
Hence, DE = AC = 30√3
In the given triangle DEB,
Tan 300 = BE/DE
1/√3 = BE/ 30√3
BE = 30m
Hence, CD = AE
= 90 - 30 = 60m
Example 2: A ground has two poles of height 30mtrs and 10mtrs on the ground. A wire connects both these poles of length 40mtrs. What is the angle made by the wire with the horizontal?
(a) 80 degree
(b) 30 degree
(c) 45 degree
(d) 90 degree
Ans: (b)
Let the two poles be AB and CD.
Let the angle made by the wire and the horizontal axis be φ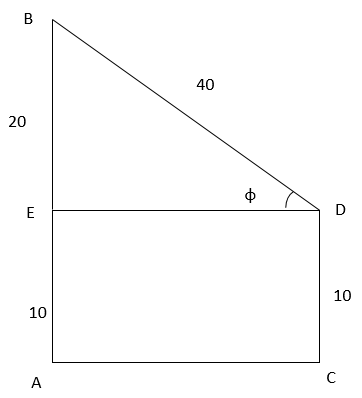
In the above triangle DEB,
Sin φ = BE/BD
= 20/40
= ½
Or, we can say
Sin φ = 300
Example 3: A building which is 20 meters high, a man is flying a kite. He is using a thread that is 75m long to keep the kite in the air. If the thread is making an angle of 450 with the horizontal, then calculate the height of the kite from the ground.
(a) 70.36 m
(b) 78.3 m
(c) 56.3 m
(d) 63.3 m
Ans: (d)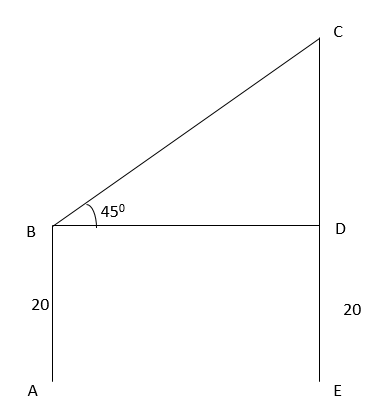
Let AB be the height of the building 20m.
Let the string be BC
In triangle BDC, the value of sin 450 = CD/BC
Or,
1/√2 = CD/BC
1/√2 = CD/ 75
CD = 43.3m
Therefore, the height of the kite is 20 + 43.3 = 63.3mtr
Example 4: A lighthouse is 80m high, a person observes two ships. The angles of elevation of both these ships as observed from the lighthouse are 450 and 300, What is the distance between the two ships?
(a) 40.36m
(b) 58.56m
(c) 89.36m
(d) None of the above
Ans: (b)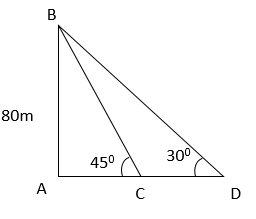
We can say that BA is the height of the lighthouse and the ships are present at points C and D.
Let CD = x
tan 450 = Perpendicular/ Hypotenuse
1 = 80/AC
AC = 80m
Therefore, AD = 80 + x
In the triangle BAD = tan 300 = AB/AD
1/√3 = 80/ (80 + x)
(80 + x) = 80√3
Therefore, x = 58.56m
Example 5: A girl is standing on the ground at a point P. If she looks at the topmost point of the building, the angle of elevation is 600. If the point P is 32 m from the building, what is its height?
(a) 30√5
(b) 20√2
(c) 32√3
(d) 90√2
Ans: (c)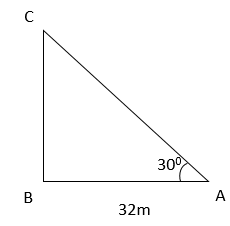
Let the building be CB, and the girl is standing at A.
AB = 32 m
In the above triangle ABC, tan 300= BC/AB
√3 = BC/AB
BC = 32√3
Therefore, the height of the building is 32√3.
Example 6: A tower is 50m high. The elevation angle to the top of the tower from the point on A on the ground is 300. Calculate the distance from the bottom of the tower and point A.
(a) 50√3
(b) 20√3
(c) 26
(d) 50√4
Ans: (a)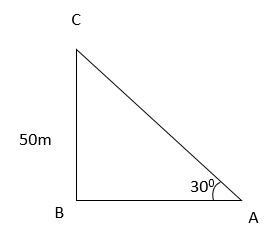
The tower of height 50m.
We have to determine the distance AB
In the given ABC, tan 300 = BC/AB
1/ √3 = 50/AB
AB = 50√3
Example 7: From the top of a building, which is 75m high, the angles of depression of the top and the bottom of a pole which is present on the same plane as the building are 300 and 450, What is the pole’s height?
(a) 75m
(b) 28.3m
(c) 32m
(d) 31.7m
Ans: (d)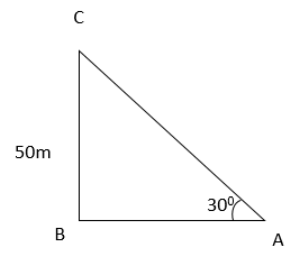
The tower of height 50m.
We have to determine the distance AB
In the given ABC, tan 300 = BC/AB
1/ √3 = 50/AB
AB = 50√3
Example 8: Raj is standing on the top of a building which is 60 meters high. The angle of elevation and depression to the top and the foot of another building are α and β. What is the height of the second building?
(a) cot β tan α
(b) 60 (1 + cot β tan α)
(c) 60 (1 + tan α)
(d) None of the above
Ans: (b)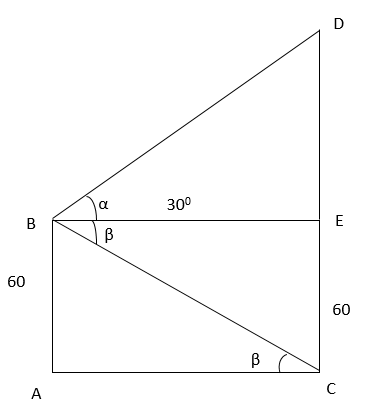
In the above figure,
ΔBAC tan β = 60/ AC
BE = AC
60/ tan β = 60 cot β
Also, in the above ΔBED
tan α = DE/ BE
tan α= DE/ 60 cot β
DE= 60 cot β tan α
Therefore, the height of the building = CD = CE + ED
= 60 + 60 cot β tan α
= 60 (1 + cot β tan α)
Example 9: A boy is standing on a riverbank. His angle of elevation from the treetop, which is on the opposite bank is 450. When he walks 20 meters away from his place, his angle of elevation becomes 300. What is the height of the tree?
(a) 7 m
(b) 5(√3 + 2)m
(c) 10(√3 + 1)m
(d) None of the above
Ans: (c)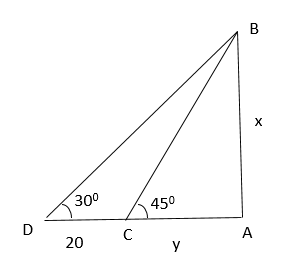
Let BA = x (height of the tree)
AC = y (river)
Let the angle of elevation at point C = 450
Angle of elevation at point D = 300
CD = 20mts
Also, in the above ΔACB,
tan 450 = x/y
1 = x/y
X = y
Also, in the given above ΔADB,
tan 300 = AB/AD
1/ √3 = x / (20 + y)
1/ √3 = x / (20 + x) (because of 1)
20 + x = √3 x
(√3– 1) x = 20
X = 20 / (√3– 1)
X = 10(√3 + 1) m
Example 10: A man is standing in his balcony, which is on the third floor of the building and is at the height of 10m. His angle of elevation at the top of the opposite building is 600, and the angle of depression of the base is 300. Determine the height of the building opposite to him?
(a) 40 mtrs
(b) 50 mtrs
(c) 70 mtrs
(d) 100 mtrs
Ans: (a)
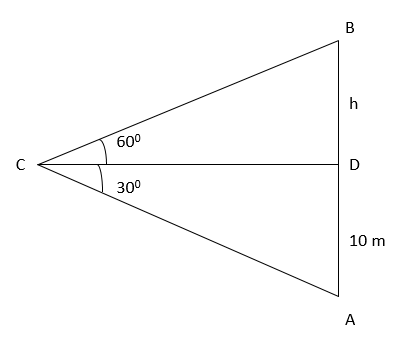 Let AB the building opposite to the man.
Let AB the building opposite to the man.
Let us assume he is standing at point C
Therefore, we can say that ∠BCD = 600
∠ACD = 300
Let BD = h
In the given ADC, tan 300 = 10/CD
1/√3= 10/CD
CD = 10 √3
Also, in the given ΔDBC, we can say that
Tan 600 = h/ CD
√3 = h/ 10 √3
H = 30 mtrs
Therefore, the height of the opposite building is
AB = BD + DA
AB = 10 + 30
AB = 40 mtrs
|
315 videos|182 docs|185 tests
|
FAQs on Solved Examples: Height & Distance - Quantitative Aptitude for SSC CGL
| 1. What is the concept of height and distance in mathematics? |  |
| 2. How can I calculate the height of a tall building using the concept of height and distance? |  |
| 3. Can height and distance be used to determine the distance between two objects? |  |
| 4. How is the concept of height and distance applied in real-life situations? |  |
| 5. Are there any practical applications of the concept of height and distance in engineering? |  |




















