Tips and Tricks: Arithmetic Progressions | Quantitative Aptitude for SSC CGL PDF Download
Arithmetic Progression Tricks
For an arithmetic progression with an initial term 'a' and a common difference 'd' between successive members, the n-th term of the sequence is expressed as
an = a+(n−1)d, where ,…n = 1,2,… and so forth.

Tips and Tricks for Arithmetic Progression To Solve Arithmetic Progression in Aptitude
An Arithmetic Progression, also known as an Arithmetic Sequence, is a sequence of numbers or terms where the difference between consecutive terms remains constant. Below are some straightforward tips and tricks to help you swiftly, easily, and efficiently solve Arithmetic Progression questions in competitive exams.
An Arithmetic Progression is Represented in the form a, (a + d), (a + 2d), (a + 3d), …
where a = the first term, and d = the common difference.
n is number of Terms
General form, Tn = a + (n-1)d
Where Tn is nth term of an Arithmetic Progression
Properties of Arithmetic Progression
- If a fixed number is added or subtracted from each term of an AP, then the resulting sequence is also an AP and it has the same common difference as that of the original AP.
- If each term in an AP is divided or multiply with a constant non-zero number, then the resulting sequence is also in an AP.
- If nth term is in linear expression then the sequence is in AP.
- If a1, a2, a3, …, an and b1, b2, b3, …, bn, are in AP. then a1+b1, a2+b2, a3+b3, ……, an+bn and a1–b1, a2–b2, a3–b3, ……, an–bn will also be in AP.
- If nth term of a series is Tn = An + B, then the series is in AP
- Three terms of the A.P whose sum or product is given should be assumed as a-d, a, a+d.
- Four terms of the A.P. whose sum or product is given should be assumed as a-3d, a-d, a+d, a+3d.
Type 1: Find nth term of series tn = a + (n − 1)d
Example 1: Find 10th term in the series 1, 3, 5, 7, …
(a) 20
(b) 19
(c) 15
(d) 21
Ans: (b)
tn = a + (n – 1)d
where tn = nth term,
a= the first term ,
d= common difference,
n = number of terms in the sequence
In the given series,
a (first term) = 1
d (common difference) = 2 (3 – 1, 5 – 3)
Therefore, 10th term = t10 = a + (n-1) d
t10 = 1 + (10 – 1) 2
t10 = 1 + 18
t10 = 19
Example 2: Find last term in the series if there are 8 term in this series 13 , 17 , 21 ,25….
(a) 33
(b) 41
(c) 37
(d) 39
Ans: (b)
We know that,
tn = a + (n – 1)d
where tn = nth term,
a = the first term ,
d = common difference,
n = number of terms in the sequence
In the given series,
a (first term) = 13
d (common difference) = 4(17 – 13, 21 – 17)
Therefore, 8th term = t8 = a + (n-1) d
t8 = 13 + (8 – 1) 4
t8 = 13 + 28
t8 = 41
Type 2: Find number of terms in the series n = 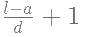
Example 1: Find the number of terms in the series 7, 11, 15, . . .71
(a) 12
(b) 25
(c) 22
(d) 17
Ans: (d)
We know that, 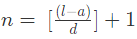
where n = number of terms,
a= the first term,
l = last term,
d= common difference
In the given series,
a (first term) = 7
l (last term) = 71
d (common difference) = 11 – 7 = 4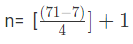
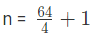
n = 16 + 1
n = 17
Example 2: Find the number of terms if First term = 22 ,Last term = 50 and common difference is 4
(a) 10
(b) 9
(c) 8
(d) 7
Ans: (c)
We know that,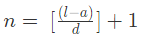
where n = number of terms,
a = the first term,
l = last term,
d = common difference
In the given series,
a (first term) = 22
l (last term) = 50
d (common difference) = 4
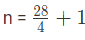
n = 7+ 1
n = 8
 |
Download the notes
Tips and Tricks: Arithmetic Progressions
|
Download as PDF |
Type 3: Find sum of first ‘n’ terms of the series
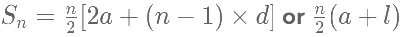
Example 1: Find the sum of the series 1, 3, 5, 7…. 201
(a) 12101
(b) 25201
(c) 22101
(d) 10201
Ans: (d)
We know that,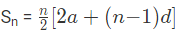
OR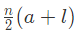
where,
a = the first term,
d= common difference,
l = tn = nth term = a + (n-1)d
In the given series,
a = 1, d = 2, and l = 201
Since we know that, l = a + (n – 1) d
201 = 1 + (n – 1) 2
201 = 1 + 2n -2
202 = 2n
n = 101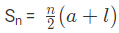
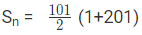
Sn = 50.5 (1 + 201)
Sn = 50.5 x 202
Sn = 10201
Example 2: Find the sum of the Arithmetic series if First term of this series is 45 , common difference is 5 and number of terms in this series is 8.
(a) 500
(b) 300
(c) 400
(d) 200
Ans: (a)
We know that,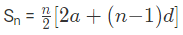
OR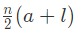
where, a = the first term,
d = common difference,
l = tn = nth term = a + (n-1)d
In the given series,
a = 45, d = 5, and n = 8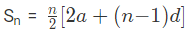
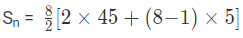
Sn = 4 (90 + 35)
Sn = 4 x 125
Sn = 500
Type 4: Find the arithmetic mean of the series. b = 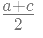
Example 1: Find the arithmetic mean of first five prime numbers.
(a) 6.6
(b) 3.6
(c) 5.6
(d) 7.6
Ans: (c)
We know that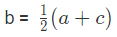
Here, five prime numbers are 2, 3, 5, 7 and 11
Therefore, their arithmetic mean (AM) 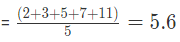
Example 2: Find Second Number if arithmetic mean of two numbers is 24 and First number is 10.
(a) 32
(b) 38
(c) 34
(d) 36
Ans: (b)
We know that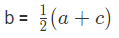
Let second Number is b
Therefore, their arithmetic mean (AM) 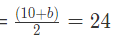
b = 38
|
315 videos|182 docs|185 tests
|
FAQs on Tips and Tricks: Arithmetic Progressions - Quantitative Aptitude for SSC CGL
| 1. What is an arithmetic progression? |  |
| 2. How can I find the nth term of an arithmetic progression? |  |
| 3. What is the formula to find the sum of an arithmetic progression? |  |
| 4. How can I determine if a given sequence is an arithmetic progression? |  |
| 5. Are there any tricks to quickly identify the common difference in an arithmetic progression? |  |


























