What are Fractions | Elementary Mathematics for CDS PDF Download
Fractions
Definition 1: A fraction represents a numerical value, which defines the parts of a whole.
Definition 2: A fraction is a number that represents a part of a whole.
Generally, the fraction can be a portion of any quantity out of the whole thing and the whole can be any specific things or value.
The basics of fractions explain the top and bottom numbers of a fraction. The top number represents the number of selected or shaded parts of a whole whereas the bottom number represents the total number of parts.
Suppose a number has to be divided into four parts, then it is represented as x/4. So the fraction here, x/4, defines 1/4th of the number x. Hence, 1/4 is the fraction here. It means one in four equal parts. It can be read as one-fourth or 1/4. This is known as fraction.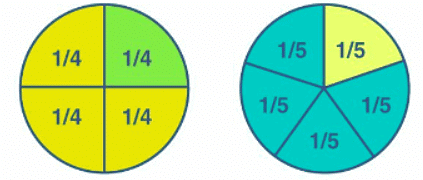
Fractions play an important part in our daily lives. There are many examples of fractions you will come across in real life. We have to willingly or unwillingly share that yummy pizza amongst our friends and families. Three people, four slices. If you learn and visualize fractions in an easy way, it will be more fun and exciting. For example, slice an apple into two parts, then each part of the sliced apple will represent a fraction (equal to 1/2).
Parts of Fractions
The fractions include two parts, numerator and denominator.
- Numerator: It is the upper part of the fraction, that represents the sections of the fraction
- Denominator: It is the lower or bottom part that represents the total parts in which the fraction is divided.
Example: If 3/4 is a fraction, then 3 is the numerator and 4 is the denominator.
Properties of Fractions
Similar to real numbers and whole numbers, a fractional number also holds some of the important properties. They are:
- Commutative and associative properties hold true for fractional addition and multiplication
- The identity element of fractional addition is 0, and fractional multiplication is 1
- The multiplicative inverse of a/b is b/a, where a and b should be non zero elements
- Fractional numbers obey the distributive property of multiplication over addition
Types of Fractions
Based on the properties of numerator and denominator, fractions are sub-divided into different types. They are:
- Proper fractions
- Improper fractions
- Mixed fractions
- Like fractions
- Unlike fractions
- Equivalent fractions
Proper Fractions
The proper fractions are those where the numerator is less than the denominator. For example, 8/9 will be a proper fraction since “numerator < denominator”.
Improper Fractions
The improper fraction is a fraction where the numerator happens to be greater than the denominator. For example, 9/8 will be an improper fraction since “numerator > denominator”.
Mixed Fractions
A mixed fraction is a combination of the integer part and a proper fraction. These are also called mixed numbers or mixed numerals. For example: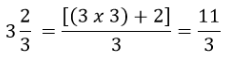
Like Fractions
Like fractions are those fractions, as the name suggests, that are alike or same.
For example, take ½ and 2/4; they are alike since if you simplify it mathematically, you will get the same fraction.
Unlike Fractions
Unlike fractions, are those that are dissimilar.
For example, ½ and 1/3 are unlike fractions.
Equivalent Fractions
Two fractions are equivalent to each other if after simplification either of two fractions is equal to the other one.
For example, ⅔ and 4/6 are equivalent fractions.
Since, 4/6 = (2×2)/(2×3) = 2/3
Unit Fractions
A fraction is known as a unit fraction when the numerator is equal to 1.
- One half of whole = 1/2
- One-third of whole = 1/3
- One-fourth of whole = 1/4
- One-fifth of whole = 1/5
Fraction on a Number Line
We have already learned to represent the integers, such as 0, 1, 2, -1, -2, on a number line. In the same way, we can represent fractions on a number line.
For example, if we have to represent 1/5 and 3/5 parts of a whole, then it can be represented as shown in the below figure.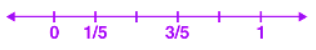
Since the denominator is equal to 5, thus 1 is divided into 5 equal parts, on the number line. Now the first section is 1/5 and the third section is 3/5.
Similarly, you can practice marking more of the fractions on the number line, such as 1/2, 1/4, 2/11, 3/7, etc.
Rules for Simplification of Fractions
There are some rules we should know before solving the problems based on fractions.
- Rule #1: Before adding or subtracting fractions, we should make sure that the denominators are equal. Hence, the addition and subtraction of fractions are possible with a common denominator.
- Rule #2: When we multiply two fractions, then the numerators are multiplied as well as the denominators are multiplied. Later simplify the fraction.
- Rule #3: When we divide a fraction from another fraction, we have to find the reciprocal of another fraction and then multiply with the first one to get the answer.
Adding Fractions
The addition of fractions is easy when they have a common denominator.
For example, ⅔ + 8/3 = (2+8)/3 = 10/3
Hence, we need to just add the numerators here.
Adding Fractions with Different Denominators
If the denominators of the two fractions are different, we have to simplify them by finding the LCM of denominators and then making it common for both fractions.
Example: ⅔ + ¾
Ans: The two denominators are 3 and 4
Hence, LCM of 3 and 4 = 12
Therefore, multiplying ⅔ by 4/4 and ¾ by 3/3, we get;
8/12 + 9/12
= (8 + 9)/12
= 17/12
Subtracting Fractions
The rule for subtracting two or more fractions is the same as for addition. The denominators should be common to subtract two fractions.
Example: 9/2 – 7/2 = (9-7)/2 = 2/2 = 1
Subtracting with Different Denominators
If the denominators of the two fractions are different, we have to simplify them by finding the LCM of denominators and then making it common for both fractions.
Example: ⅔ – ¾
Ans: The two denominators are 3 and 4
Hence, LCM of 3 and 4 = 12
Therefore, multiplying ⅔ by 4/4 and ¾ by 3/3, we get;
8/12 – 9/12
= (8 - 9)/12
= -1/12
Multiplication of Fractions
As per rule number 2, we have discussed in the previous section, when two fractions are multiplied, then the top part (numerators) and the bottom part (denominators) are multiplied together.
If a/b and c/d are two different fractions, then the multiplication of a/b and c/d will be:
(a/b) x (c/d) = (axc)/(bxd) = (ac/bd)
Example: Multiply ⅔ and 3/7.
Ans: (⅔) x (3/7) = (2×3)/(3×7) = 2/7
Division of Fractions
If we have to divide any two fractions, then we will use here rule 3 from the above section, where we need to multiply the first fraction to the reciprocal of the second fraction.
If a/b and c/d are two different fractions, then the division a/b by c/d can be expressed as:
(a/b) ÷ (c/d) = (a/b) x (d/c) = (ad/bc)
Example: Divide ⅔ by 3/7.
(⅔) ÷ (3/7) = (⅔) x (7/3) = (2×7)/(3×3) = 14/9
Real-Life Examples of Fractions
Let us visualize some of the fractions examples:
- Imagine a pie with four slices. Taking two slices of pie for yourself would mean that you have two out of the four. Hence, you represent it as 2/4.
- Fill half a glass of water. What do you see? 1/2 glass is full. Or 1/2 glass is empty. This 1/2 is fractions where 1 is the numerator that is, the number of parts we have. And 2 is the denominator, the number of parts the whole glass is divided into.
How to Convert Fractions To Decimals?
As we already learned enough about fractions, which are part of a whole. The decimals are the numbers expressed in a decimal form which represents fractions, after division.
For example, Fraction 1/2 can be written in decimal form as 0.5.
The best part of decimals are they can be easily used for any arithmetic operations such as addition, subtraction, etc. Whereas it is difficult sometimes to perform operations on fractions. Let us take an example to understand;
Example: Add 1/6 and 1/4.
Ans: 1/6 = 0.17 and 1/4 = 0.25
Hence, on adding 0.17 and 0.25, we get;
0.17 + 0.25 = 0.42
How to Simplify Fractions?
To simplify a fraction efficiently, start by listing the factors of both the numerator and denominator. Identify the largest factor shared by both. Divide both the numerator and denominator by this greatest common factor (GCF) to obtain the reduced fraction, which represents the simplest form of the original fraction. Let's take an example to illustrate this process.
For example, take the fraction, 16/48
So, the factors of 16 are 1, 2, 4, 8, 16.
Similarly, the factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
Thus, the greatest common factor for 16 and 48 is 16.
i.e. GCF (16, 48) = 16.
Now, divide both the numerator and denominator of the given fraction by 16, we get
16/48 = (16/16) / (48/16) = 1/3.
Hence, the simplest form of the fraction 16/48 is 1/3.
Solved Examples on Fractions
Example 1: Which of the following fraction is the largest?
(a) 29/23
(b) 29/27
(c) 29/25
(d) 29/30
Ans: To find whether the largest fractions among the given options, first convert the fractional value to the decimal value.
(a) 29/23 = 1.261
(b) 29/27 = 1.074
(c) 29/25 = 1.16
(d) 29/30 = 0.967
Thus, 29/23 is the largest fraction among the given options.
Hence, option (a) 29/23 is the correct answer.
Example 2: Reduce the fraction 15/65 to the simplest form.
Ans: Given fraction: 15/65.
Factors of 15: 1, 3, 5 and 15
Factors of 65: 1, 5, 13, and 65
Hence, the greatest common factor of 15 and 65 is 5.
i.e. GCF (15, 65) = 5.
Now, divide both the numerator and the denominator of the given fraction (16/65) by 5, we get
15/65 = (15/5) / (65/5) = 3/13.
Hence, the simplest form of the fraction 15/65 is 3/13.
Example 3: Is 12/6 a fraction?
Ans: Yes, it is. It is called an improper fraction.
Example 4: Convert 130.1200 into a fraction.
Ans: Here will use the concept of how to convert decimals into fractions
130.1200 = 130.1200/10000
= 13012/100
Example 5: Add 3/ 5 and 10/15.
Ans: 3 /5 + 10/15
LCM of 5 and 15 is 15
= (9 + 10)/15
= 19/15
|
165 videos|95 docs|127 tests
|
















