Lattice Energy & Born-Haber cycle | Chemistry Optional Notes for UPSC PDF Download
| Table of contents |

|
| Introduction |

|
| Considerations |

|
| What Is the Born Haber Cycle? |

|
| Solved Examples |

|
Introduction
- The Born Haber process, more commonly referred to as the Born Haber cycle, is a method that allows us to observe and analyse energies in a reaction. It mainly helps in describing the formation of ionic compounds from different elements. The methodology further enables us to understand the overall reaction process through a series of steps.
- The Born Haber cycle was introduced in the year 1919 by German scientists Fritz Haber and Max Born. The Born Haber cycle is mainly used to calculate the lattice energy. It also involves several steps or processes, such as electron affinity, ionization energy, sublimation energy, the heat of formation and dissociation energy.
Considerations
- The reaction of electropositive metals with electronegative nonmetals produces ionic solids. Alkali and alkaline earth metals react with chalcogen or halogen family elements to form compounds, which are crystalline ionic solids. Ionic compounds being stabilized by the electrostatic force of attraction between positive and negative charges are expected to have similar physical properties.
- But physical properties like stability and the water solubility of these ionic compounds differ much. The difference is attributed to the difference in an enthalpy called ‘Lattice energy’ between the ionic solids.
- Lattice energy is the energy that keeps together the cations and anions of the compound in fixed positions in a crystalline solid state. Lattice energy can be defined as either energy released when gaseous ions form one mole of a solid ionic compound or as the energy required to convert one mole ionic solid into its gaseous ions. There is no way to measure this lattice energy experimentally. Hess’s law of heat summation is the only indirect way of estimating the lattice energy.
- Application of Hess’s law of heat summation to the formation of solid ionic compounds involves enthalpy of all processes that are necessary for the formation of the solid ionic compound from the elemental state of the constituent atoms in a form cycle such that the total energy on summation is zero.
What Is the Born Haber Cycle?
The Born Haber cycle is a cycle of enthalpy change of process that leads to the formation of a solid crystalline ionic compound from the elemental atoms in their standard state and of the enthalpy of formation of the solid compound such that the net enthalpy becomes zero.
 |
Download the notes
Lattice Energy & Born-Haber cycle
|
Download as PDF |
Solved Examples
Example 1: Born Haber cycle of sodium chloride NaCl (or any AB-type Mono-valent ionic solid).
The heat of the formation of sodium chloride (ΔHf0) from the sodium metal and chlorine gas can be experimentally measured.
Na (s) + (1/2)Cl2 (g) → NaCl(s) ΔHf0 = -411kJ/mol
The formation of ionic solid sodium chloride from solid sodium metal and gaseous chlorine is not a single-step process but goes through several processes. Heat changes of all the processes except the lattice energy can be experimentally measured.
The processes or steps in the formation of sodium chloride are as follows:
- Solid sodium atom sublimes to gaseous atom by absorbing heat energy (∆Hsub).
Na (s) → Na (g),
Sublimation energy ΔHsub = + 107kJ/mol - Gaseous sodium atom absorbs the ionization energy to release one electron and forms a gaseous sodium ion.
Na(g) → Na+(g) + 1e– ,
Ionization energy ∆HIE = +502kJ/mol - Diatomic gaseous chlorine breaks into two individual atoms by absorbing bond energy, such that each chlorine atom absorbs half of the bond energy of the chlorine molecule.
Cl2(g) → 2Cl(g) (1/2)
Bond dissociation energy of chlorine = (1/2) ∆Hdiss= (1/2) 242 = +121kJ/mol - Chlorine atom accepts an electron to form a chloride ion and releases energy equivalent to electron affinity.
Cl(g) + 1e– → Cl– (g)
Electron affinity = ∆HEA = -355kJ/mol - Gaseous sodium ion and gaseous chloride ion combine to form a solid sodium chloride molecule and releases energy equivalent to lattice energy.
Na+(g) + Cl– (g) → Na+ Cl– (s)
Lattice energy = ∆HLE = U = ?
The summation of enthalpy of all the processes (from step 1 to step 5) give the net enthalpy of the formation of solid crystalline sodium chloride from sodium and chlorine in their standard conditions of solid and gas, respectively. This should be equal to the experimentally measured enthalpy of the formation of solid sodium chloride. The enthalpies are represented as a cycle in the figure.
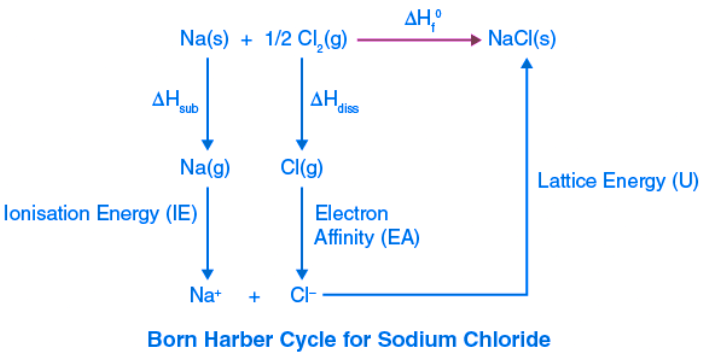
So, ΔHf0 = ΔHsub + ∆HIE + (1/2) ∆Hdis + ∆HEA + U or ΔHf0 – (ΔHsub + ∆HIE + (1/2) ∆Hdis + ∆HEA + U)=0
411 + 107 + 502 +121 -355 +U = 0
Here, except lattice energy, all other enthalpies can be experimentally measured.
The lattice energy of the sodium chloride solid = U = ΔHf0 – (ΔHsub + ∆HIE + ½ ∆Hdis + ∆HEA).
= -411 -107 -502 -121 +355
= – 786kJ/mol
Example 2: Lattice energy of magnesium oxide (or any AB-type Divalent ionic solid).
The heat of the formation of magnesium oxide (ΔHf0) from the magnesium metal and oxygen gas can be experimentally measured.
Mg (s) + (1/2) O2 (g) → MgO(s)
ΔHf0 = -602kJ/mol
The processes or steps in the formation of magnesium oxide are as follows:
- Solid magnesium atom sublimes to a gaseous atom by absorbing heat energy (∆Hsub).
Mg (s) → Mg (g), Sublimation energy ΔHsub = + 136kJ/mol - Gaseous magnesium atom releases two electrons in two steps with corresponding ionization energies.
Mg(g) → Mg+(g) + 1e–, ionization energy ∆H1IE= +738kJ/mol
Mg+(g) → Mg2+(g) + 1e–, ionization energy ∆H2IE= +1450kJ/mol
So energy of ionization = ∆HIE = 738 + 1450 = 2188kJ/mol. - Diatomic oxygen breaks into two individual atoms by absorbing bond energy, such that each chlorine atom absorbs half of the bond energy of the chlorine molecule.
O2(g) → 2O(g) (1/2) bond dissociation energy of oxygen = (1/2) ∆Hdiss= (1/2) 498 = +249kJ/mol - Oxygen atom accepts two electrons to form an oxide ion and releases energy equivalent to two-electron affinities.
O(g) + 1e– → O– (g) Electron affinity = ∆H1EA = -142kJ/mol
O–(g) + 1e– → O2- (g) Electron affinity = ∆H2EA = +798kJ/mol
The total energy released as electron affinity by the oxygen atom is = ∆HEA = +656kJ/mol - Gaseous magnesium ion and gaseous oxide ion combine to form a solid magnesium oxide molecule and releases energy equivalent to lattice energy.
Mg2+(g) + O2- (g) → Mg2+O2- (s) Lattice energy = ∆HLE = U = ?
The summation of enthalpy of all the processes from the starting step to the final step gives the net enthalpy of the formation of solid crystalline magnesium oxide from magnesium and oxygen in their standard conditions of solid and gas, respectively. This should be equal to the experimentally measured enthalpy of the formation of solid magnesium oxide. The enthalpies are represented as a cycle in the figure.
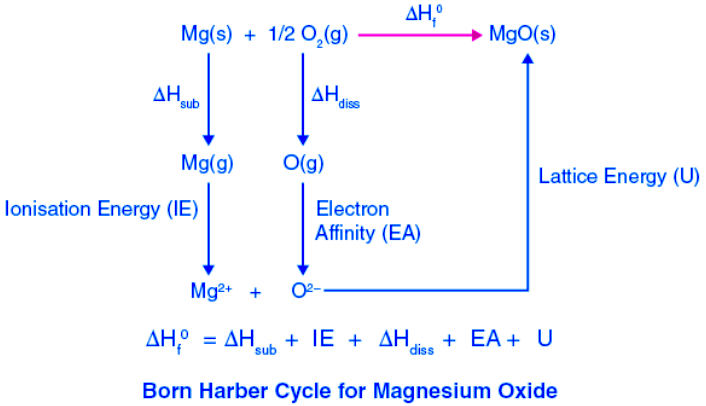
So, ΔHf0 = ΔHsub + ∆HIE + (1/2) ∆Hdis + ∆HEA + U or ΔHf0 – (ΔHsub + ∆HIE + (1/2) ∆Hdis + ∆HEA + U) = 0
602 + 136 + 2188 + 249 +656 + U = 0
Here, except lattice energy, all other enthalpies can be experimentally measured.
The lattice energy of the magnesium oxide solid = U = ΔHf0 – (ΔHsub + ∆HIE + (1/2) ∆Hdis + ∆HEA).
= -602 – 136 – 2188 – 249 -656 = -3831kJ/mol
FAQs on Lattice Energy & Born-Haber cycle - Chemistry Optional Notes for UPSC
| 1. What is the significance of the Born Haber cycle in understanding lattice energy? |  |
| 2. How does the Born Haber cycle help in determining the lattice energy of a compound? |  |
| 3. Can the Born Haber cycle be used to predict the stability of an ionic compound? |  |
| 4. What are the factors that influence the lattice energy of an ionic compound? |  |
| 5. Can the Born Haber cycle be applied to covalent compounds as well? |  |


















