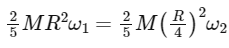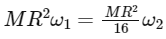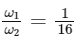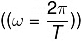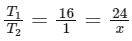[JEE Mains MCQs]
Q1: Two identical particles each of mass 'm' go round a circle of radius a under the action of their mutual gravitational attraction. The angular speed of each particle will be:
(a) 
(b) 
(c)
(d) 
Ans: (d)
The gravitational force between two particles of mass m separated by a distance r is given by:

where G is the gravitational constant. In this problem, the two particles are moving in a circular orbit of radius a under the influence of their mutual gravitational attraction. Therefore, the gravitational force between the two particles provides the necessary centripetal force to keep them in circular motion.
The centripetal force required for a particle of mass m moving in a circle of radius a with angular speed ω is given by:
Fcentripetal = mω2a
Setting the gravitational force equal to the centripetal force, we get:

Substituting r = 2a (since the two particles are separated by a distance equal to twice the radius of the circle), we get:

Simplifying, we get:

Taking the square root of both sides, we get:

Therefore, the angular speed of each particle is 
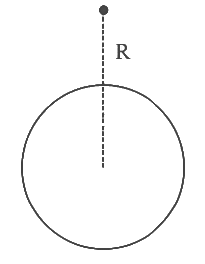
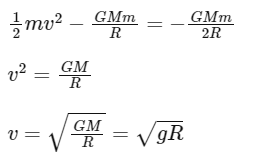
Q2: A body is released from a height equal to the radius (R) of the earth. The velocity of the body when it strikes the surface of the earth will be (Given g = acceleration due to gravity on the earth.)
(a) 
(b) 
(c) 
(d) 
Ans: (d)
 By conservation of mechanical energy
By conservation of mechanical energy

Q3: Given below are two statements:
Statement I : For a planet, if the ratio of mass of the planet to its radius increases, the escape velocity from the planet also increases.
Statement II : Escape velocity is independent of the radius of the planet.
In the light of above statements, choose the most appropriate answer form the options given below
(a) Both Statement I and Statement II are correct
(b) Statement I is correct but statement II is incorrect
(c) Both Statement I and Statement II are incorrect
(d) Statement I is incorrect but statement II is correct
Ans: (b)
Statement I suggests that the escape velocity of a planet increases with an increase in the ratio of its mass to its radius. This statement is consistent with the formula for escape velocity, which shows that the escape velocity of a planet is directly proportional to the square root of its mass and inversely proportional to the square root of its radius.
On the other hand, Statement II suggests that the escape velocity is independent of the radius of the planet. This statement is not consistent with the formula for escape velocity, which clearly shows that the escape velocity is inversely proportional to the square root of the radius of the planet.
Hence, the most appropriate answer is: Statement I is true, but Statement II is false.
Q4: Two planets A and B of radii R and 1.5 R have densities ρ and ρ/2 respectively. The ratio of acceleration due to gravity at the surface of B to A is:
(a) 2 : 1
(b) 2 : 3
(c) 4 : 3
(d) 3 : 4
Ans: (d)
The acceleration due to gravity at the surface of a planet is given by the formula:

where G is the gravitational constant, M is the mass of the planet, A and R is the radius of the planet. In this problem, we are given two planets A and B, with radii RA and RB = 1.5 RA, and densities ρA and ρB = ρA/2 , respectively. We can use the formula above to calculate the acceleration due to gravity at the surface of each planet:


To find the ratio of the accelerations due to gravity at the surfaces of planets A and B, we can divide the expression for gB by the expression for gA:

So, we can see that the acceleration due to gravity at the surface of planet B is 3/2 times larger than that at the surface of planet A.
However, the question asks for the ratio of the gravitational accelerations at the surfaces of the planets, which is equal to the ratio of the densities times the ratio of the radii:

Therefore, the ratio of the gravitational accelerations at the surfaces of the planets is 3/4, which is our final answer.
Q5: A planet having mass 9 Me and radius 4Re, where Me and Re are mass and radius of earth respectively, has escape velocity in km / s given by: (Given escape velocity on earth Ve = 11.2 × 103 m /s)
(a) 33.6
(b) 11.2
(c) 16.8
(d) 67.2
Ans: (c)
The escape velocity on a planet is given by the following formula:

where vesc is the escape velocity, G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.
For Earth, we are given that ve = 11.2 × 103 m/s. We know that the mass of the planet in question is 9Me and its radius is 4Re. Let's find the escape velocity of this planet:

Divide both sides by the Earth's escape velocity formula:

Simplify:

Now, solve for vesc:


Converting this to km/s, we get:
vesc = 16.8 km/s
Q6: The ratio of escape velocity of a planet to the escape velocity of earth will be:-
Given: Mass of the planet is 16 times mass of earth and radius of the planet is 4 times the radius of earth.
(a) 1 : 4
(b) 1 : √2
(c) 4 : 1
(d) 2 : 1
Ans: (d)
The escape velocity of a planet or a celestial body is given by:

where G is the gravitational constant, M is the mass of the planet, and r is the radius of the planet.
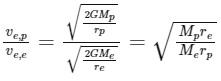
Let the subscripts "p" and "e" denote the planet and earth, respectively. Then, we have:

Substituting the given values, we get:

Therefore, the ratio of the escape velocity of the planet to that of earth is 2 : 1.
Q7: Two satellites A and B move round the earth in the same orbit. The mass of A is twice the mass of B. The quantity which is same for the two satellites will be
(a) Potential energy
(b) Kinetic energy
(c) Total energy
(d) Speed
Ans: (d)
The quantity which is same for the two satellites will be speed.
The orbital speed of a satellite is independent of the mass of the satellite, but it depends on the radius of the orbit. Potential energy, kinetic energy and total energy depend on the mass of the the satellite.
Therefore, the only quantity that is the same for the two satellites is speed.
Q8: A space ship of mass 2 × 104 kg is launched into a circular orbit close to the earth surface. The additional velocity to be imparted to the space ship in the orbit to overcome the gravitational pull will be (if g = 10 m / s2 and radius of earth = 6400 km):
(a) 7.9 (√2 − 1) km/s
(b) 11.2 (√2 − 1) km/s
(c) 7.4 (√2 − 1) km/s
(d) 8 (√2 − 1) km/s
Ans: (d)
To find the additional velocity required to overcome the gravitational pull and launch the spaceship into orbit, we first need to find the orbital velocity. The formula for orbital velocity (v) is given by:

where G is the gravitational constant, M is the mass of Earth, and r is the distance from the center of the Earth to the spaceship (which is the sum of the Earth's radius and the altitude of the spaceship's orbit).
In this problem, the spaceship is orbiting close to Earth's surface, so we can approximate r as the Earth's radius. Given that g = 10 m/s² and Earth's radius R = 6400 km, we can relate the gravitational constant G and the mass of Earth M through the formula:

Now, we can find the orbital velocity:

Converting the Earth's radius to meters:

Plugging in the values:

Now, we need to find the additional velocity required to overcome the gravitational pull. To do this, we can use the formula for escape velocity:

Finding the additional velocity required:

Plugging in the values:

Converting the velocity to km/s:

Thus, the additional velocity required to overcome the gravitational pull and launch the spaceship into orbit is: 8 (√2 − 1) km/s
Q9: If V is the gravitational potential due to sphere of uniform density on it's surface, then it's value at the center of sphere will be:-
(a) 3V/2
(b) V/2
(c) 4/3 V
(d) V
Ans: (a)
The gravitational potential (V) due to a sphere of uniform density at a distance r from its center is given by:

At the surface of the sphere (r = R), the gravitational potential is:

Now, let's find the gravitational potential at the center of the sphere (r = 0):

The gravitational potential at the center of the sphere is 3/2 times the potential at the surface of the sphere. Therefore: V(0) = 3V/2
Q10: The radii of two planets 'A' and 'B' are 'R' and '4R' and their densities are ρ and ρ/3 respectively. The ratio of acceleration due to gravity at their surfaces (gA : gB) will be:
(a) 3 : 16
(b) 4 : 3
(c) 1 : 16
(d) 3 : 4
Ans: (d)
The acceleration due to gravity at the surface of a planet can be expressed as: g ∝ ρR
Now let's find the ratio of acceleration due to gravity at the surfaces of planets A and B:

Given that the densities are ρ and ρ/3 and the radii are R and 4R for planets A and B, respectively, we have:

So, the ratio of acceleration due to gravity at their surfaces is 3 : 4
Q11: The time period of a satellite, revolving above earth's surface at a height equal to R will be
(Given g = π2 m/s2 , R = radius of earth)
(a) 
(b) 
(c) 
(d) 
Ans: (a)
For a satellite orbiting the Earth at a height equal to Earth's radius, its distance from the center of the Earth will be 2R, where R is the radius of the Earth.
Using the formula for the gravitational force:

where F is the gravitational force, G is the gravitational constant, M is the mass of the Earth, m is the mass of the satellite, and r is the distance from the center of the Earth.
The centripetal force acting on the satellite is given by:

Equating the gravitational force and the centripetal force, we get:

Solving for the orbital speed v, we get:

The circumference of the satellite's orbit is given by:

The time period T of the satellite's orbit can be calculated as the ratio of the circumference to the orbital speed:

Given that the acceleration due to gravity at the Earth's surface is g = π2 m/s2, we can express the gravitational constant G in terms of the Earth's radius R and mass M:

Substituting the expression for GM into the equation for the time period T, we get:

Multiplying the numerator and denominator by √2, we get:

Q12: Given below are two statements:
Statement I : Rotation of the earth shows effect on the value of acceleration due to gravity (g)
Statement II : The effect of rotation of the earth on the value of 'g' at the equator is minimum and that at the pole is maximum.
In the light of the above statements, choose the correct answer from the options given below
(a) Statement I is false but statement II is true
(b) Statement I is true but statement II is false
(c) Both Statement I and Statement II are true
(d) Both Statement I and Statement II are false
Ans: (b)
Statement I: The rotation of the Earth does indeed have an effect on the value of acceleration due to gravity (g). The rotational motion of the Earth causes a centrifugal effect which reduces the net acceleration due to gravity slightly. This effect is most pronounced at the equator and least pronounced at the poles due to the geometry of Earth's rotation.
Statement II: This statement is incorrect. The effect of Earth's rotation on the value of 'g' is maximum at the equator, not minimum. This is because the centrifugal force due to Earth's rotation is directed outward and is maximal at the equator, where the rotational speed is greatest. This outward force reduces the net gravitational acceleration one would experience at the equator. At the poles, there is no centrifugal force due to rotation, so the acceleration due to gravity is not reduced. Hence, the net effect of Earth's rotation on 'g' is least (essentially zero) at the poles, not maximum.
Q13: Two satellites of masses m and 3m revolve around the earth in circular orbits of radii r & 3r respectively. The ratio of orbital speeds of the satellites respectively is
(a) 3 : 1
(b) √3 : 1
(c) 1 : 1
(d) 9 : 1
Ans: (b)
The orbital speed of an object moving in a circular orbit around Earth (or any other celestial body) is given by the formula:

where (v) is the orbital speed, (G) is the gravitational constant, (M) is the mass of the central body (Earth, in this case), and (r) is the radius of the orbit.
For the two satellites of masses (m) and (3m) in orbits of radii (r) and (3r) respectively, the ratio of their orbital speeds (v1 / v2) is:

So, the ratio of the orbital speeds of the satellites is (√3 : 1), which corresponds to Option B.
This calculation is independent of the masses of the satellites, as the mass of the satellite does not affect its orbital speed. The orbital speed is determined by the mass of the central body (Earth) and the radius of the orbit.
Q14: Assuming the earth to be a sphere of uniform mass density, the weight of a body at a depth d = R/2 from the surface of earth, if its weight on the surface of earth is 200 N, will be:
(Given R = radius of earth)
(a) 100 N
(b) 400 N
(c) 300 N
(d) 500 N
Ans: (a)
The gravitational field strength, or equivalently, the weight of an object, decreases linearly from its surface value to zero at the center of a sphere of uniform mass density. This is because only the mass inside the radius at which the object is located contributes to the gravitational force at that location.
If (d = R/2) is the depth below the surface of the Earth, then the radius of the sphere contributing to the gravitational force at that depth is ( )
)
Since the gravitational force (or weight) decreases linearly with the radius in a sphere of uniform density, the weight of the object at depth (d = R/2) is half its weight at the surface of the Earth.
So, if the weight of the body on the surface of the Earth is 200 N, its weight at depth (d = R/2) is half of that, or 100 N.
Therefore, the correct answer is 100 N.
Q15: The acceleration due to gravity at height h above the earth if h << R (Radius of earth) is given by
(a) 
(b) 
(c) 
(d) 
Ans: (a)
The acceleration due to gravity (g) at the surface of Earth is approximately m/s 9.81 m/s2. This acceleration decreases as we move away from the Earth's surface because gravity is a force that attracts objects towards the center of the Earth. This force decreases with the square of the distance from the center of the Earth, due to the inverse square law.
However, if we are at a height (h) much less than the radius of the Earth (R), we can use a linear approximation to calculate the new acceleration due to gravity (g′) at this height. This is because for small heights compared to the radius of Earth, the decrease in g can be approximated to be linear. This is represented by the following formula:

Here's how this formula is derived:
The force of gravity (F) is given by the universal law of gravitation:

where:
G is the gravitational constant, m1 and m2 are the masses of the two objects (in this case, the Earth and the object we're considering), d is the distance between the centers of the two objects.
If we consider an object of mass m at the surface of Earth, the force it experiences due to gravity is:

where:
M is the mass of Earth,
R is the radius of Earth,
 is the acceleration due to gravity at the Earth's surface.
is the acceleration due to gravity at the Earth's surface.
Now, if the object is at a height h above the Earth's surface, the force it experiences is:

We can write and because h << R , we can use the binomial approximation (1 + x)2 ≈ 1 + 2x for small x to get:
and because h << R , we can use the binomial approximation (1 + x)2 ≈ 1 + 2x for small x to get:

Equating the forces F = mg and F′ = mg′ gives us:

Q16: The orbital angular momentum of a satellite is L, when it is revolving in a circular orbit at height h from earth surface. If the distance of satellite from the earth centre is increased by eight times to its initial value, then the new angular momentum will be -
(a) 9L
(b) 8L
(c) 4L
(d) 3L
Ans: (d)
If we take the velocity (v) of the satellite to be  , where G is the gravitational constant, M is the mass of the Earth, and r is the distance from the center of the Earth to the satellite, then the orbital angular momentum (L) is:
, where G is the gravitational constant, M is the mass of the Earth, and r is the distance from the center of the Earth to the satellite, then the orbital angular momentum (L) is:

If the distance (r) from the Earth's center is increased by a factor of 8, the new angular momentum L′ is: 
However, the distance from the earth's surface is given, so we have to take into account the radius of the Earth (R) in our calculations. When the height from the earth's surface is increased eight times, the distance from the earth's center is r = R + 8h, which is approximately 9R (because the height of the satellite above the Earth is generally much less than the radius of the Earth).
So, the new angular momentum (L'') is:

Q17: Given below are two statements:
Statement I: If E be the total energy of a satellite moving around the earth, then its potential energy will be E/2.
Statement II: The kinetic energy of a satellite revolving in an orbit is equal to the half the magnitude of total energy E.
In the light of the above statements, choose the most appropriate answer from the options given below
(a) Both Statement I and Statement II are incorrect
(b) Statement I is incorrect but Statement II is correct
(c) Statement I is correct but Statement II is incorrect
(d) Both Statement I and Statement II are correct
Ans: (a)
A satellite in orbit around a planet is subject to two main forces: gravitational force, which is trying to pull it towards the planet, and its own kinetic energy or inertia, which is trying to keep it moving in a straight line. The balance of these two forces results in the satellite moving in a circular or elliptical orbit.
The gravitational potential energy (U) of the satellite is given by the formula:

where G is the gravitational constant, M is the mass of the Earth, m is the mass of the satellite, and R is the radius of the orbit.
The negative sign indicates that work would have to be done to remove the satellite from the Earth's gravitational influence.
The kinetic energy (K) of the satellite is given by the formula:

This is obtained from the fact that for a satellite in stable orbit, the gravitational force must be equal to the centripetal force required to keep the satellite moving in a circle. From this, we can derive an expression for the velocity of the satellite, and hence its kinetic energy.
The total mechanical energy (E) of the satellite, which is the sum of its kinetic and potential energy, is therefore:

So the potential energy U is − 2E , and the kinetic energy K is − E. Thus, the statement "If E be the total energy of a satellite moving around the earth, then its potential energy will be 2E" is correct, and the statement "The kinetic energy of a satellite revolving in an orbit is equal to the half the magnitude of total energy E" is incorrect.
Q18: The weight of a body on the earth is 400 N. Then weight of the body when taken to a depth half of the radius of the earth will be:
(a) 300 N
(b) 200 N
(c) 100 N
(d) Zero
Ans: (b)
The gravitational field inside a uniform spherical body varies linearly with distance from the center. If we consider the Earth to be such a body, then the gravitational field strength (and hence weight) of an object would decrease linearly as we go deeper inside the Earth.
The weight of an object at a depth d from the Earth's surface is given by:

where:
Wd is the weight at depth d ,
We is the weight at the Earth's surface (i.e., the weight of the object), and
R is the radius of the Earth.
In this case, we're given that We = 400 N , and we're asked to find the weight at a depth of d = R/2. Substituting these values into the formula, we get:

Therefore, the weight of the body when taken to a depth half of the radius of the Earth is 200 N.
Q19: The weight of a body on the surface of the earth is 100 N. The gravitational force on it when taken at a height, from the surface of earth, equal to one-fourth the radius of the earth is:
(a) 50 N
(b) 64 N
(c) 25 N
(d) 100 N
Ans: (b)
To find the gravitational force on the body when taken at a height equal to one-fourth the radius of the Earth, we can use the formula for gravitational force:

where F is the gravitational force, G is the gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between their centers.
The weight of the body on the surface of the Earth is given as N 100 N , which is also the gravitational force acting on it:

When the body is taken to a height equal to one-fourth the radius of the Earth, the distance between the centers of the body and the Earth becomes

Now the gravitational force acting on the body at this new height is:

To find the ratio between the new gravitational force and the original force on the surface, we can write:

Canceling out the common terms, we get:

Now, since the weight of the body on the surface is N 100 N , we can find the new gravitational force as:

So, the gravitational force on the body when taken at a height equal to one-fourth the radius of the Earth is N 64 N.
Q20: Choose the incorrect statement from the following:
(a) The linear speed of a planet revolving around the sun remains constant.
(b) When a body falls towards earth, the displacement of earth towards the body is negligible.
(c) The speed of satellite in a given circular orbit remains constant.
(d) For a planet revolving around the sun in an elliptical orbit, the total energy of the planet remains constant.
Ans: (a)
The linear speed of a planet revolving around the sun does not remain constant, as planets follow an elliptical orbit around the sun. According to Kepler's second law, the areal velocity of a planet remains constant, which means that the planet moves faster when it is closer to the sun (at perihelion) and slower when it is farther away (at aphelion).
Q21: Given below are two statements : one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: Earth has atmosphere whereas moon doesn't have any atmosphere.
Reason R: The escape velocity on moon is very small as compared to that on earth. In the light of the above statements, choose the correct answer from the options given below:
(a) A is false but R is true
(b) Both A and R are correct but R is NOT the correct explanation of A
(c) Both A and R are correct and R is the correct explanation of A
(d) A is true but R is false
Ans: (c)
The assertion (A) is true: Earth does have an atmosphere, while the Moon does not have a significant atmosphere.
The reason (R) is also true: The escape velocity on the Moon is indeed smaller than that on Earth. The escape velocity is the minimum velocity an object must have to escape the gravitational pull of a planet or moon. A smaller escape velocity means it's easier for particles (such as the particles that make up an atmosphere) to escape into space.
Additionally, the reason (R) is a correct explanation for the assertion (A). The fact that the Moon's escape velocity is smaller than the Earth's is a major reason why the Moon doesn't have a significant atmosphere. Over time, particles that could have made up an atmosphere have escaped the Moon's gravitational pull and dispersed into space.
Q22: A planet has double the mass of the earth. Its average density is equal to that of the earth. An object weighing W on earth will weigh on that planet:
(a) 22/3 W
(b) W
(c) 2 W
(d) 21/3 W
Ans: (d)
The weight of an object on a planet is given by the equation W = mg, where m is the mass of the object and g is the acceleration due to gravity.
The acceleration due to gravity on a planet is given by the equation where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.
where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.
In this case, the mass of the planet is double that of Earth (M = 2ME), but the density is the same. Density is defined as mass divided by volume, so if the mass is doubled and the density stays the same, the volume must also double.
Since the volume of a sphere (like a planet) is given by the equation  a doubling of the volume implies that the radius of the planet is
a doubling of the volume implies that the radius of the planet is 
Substituting these values back into the equation for g, we get:

So the weight of the object on the planet is

Q23: The escape velocities of two planets A and B are in the ratio 1 : 2. If the ratio of their radii respectively is 1 : 3 , then the ratio of acceleration due to gravity of planet A to the acceleration of gravity of planet B will be:
(a) 4/3
(b) 2/3
(c) 3/4
(d) 3/2
Ans: (c)
The escape velocity of a planet is given by the formula:

where G is the gravitational constant, M is the mass of the planet, and R is its radius.
If the escape velocity of planet A is vA and the escape velocity of planet B is vB, then we can write the following relationship:

We know, The acceleration due to gravity on a planet can be calculated using the formula:

where G is the gravitational constant, M is the mass of the planet, and R is its radius.

Q24: For a body projected at an angle with the horizontal from the ground, choose the correct statement.
(a) Gravitational potential energy is maximum at the highest point.
(b) The vertical component of momentum is maximum at the highest point.
(c) The horizontal component of velocity is zero at the highest point.
(d) The Kinetic Energy (K.E.) is zero at the highest point of projectile motion.
Ans: (a)
At highest point height is maximum and vertical component of velocity is zero.
So momentum is zero.
At highest point horizontal component of velocity will not be zero but vertical component of velocity is equal to zero and because of this K.E. will not be equal to zero.
Gravitational potential energy is maximum at highest point and equal to mgH = 
Q25: If earth has a mass nine times and radius twice to that of a planet P. Then  will be the minimum velocity required by a rocket to pull out of gravitational force of P , where ve is escape velocity on earth. The value of x is
will be the minimum velocity required by a rocket to pull out of gravitational force of P , where ve is escape velocity on earth. The value of x is
(a) 1
(b) 3
(c) 2
(d) 18
Ans: (c)
ME =9MP
RE = 2RP


Q26: Given below are two statements:
Statement I: Acceleration due to gravity is different at different places on the surface of earth.
Statement II: Acceleration due to gravity increases as we go down below the earth's surface. In the light of the above statements, choose the correct answer from the options given below
(a) Both Statement I and Statement II are true
(b) Both Statement I and Statement II are false
(c) Statement I is false but Statement II is true
(d) Statement I is true but Statement II is false
Ans: (d)
Statement I is true. The acceleration due to gravity varies slightly over the surface of the Earth, being affected by factors such as latitude (because of the Earth's oblate shape or its equatorial bulge), altitude (it decreases with height above the Earth's surface), and local geological variations in the Earth's density.
Statement II is false. The acceleration due to gravity actually decreases as we go down below the Earth's surface. This is because the mass that is "above" or outside the location begins to pull the object away from the Earth's center, and the net gravitational acceleration decreases.
Therefore, Option D: Statement I is true but Statement II is false, is the correct answer.
Q27: A body weight W, is projected vertically upwards from earth's surface to reach a height above the earth which is equal to nine times the radius of earth. The weight of the body at that height will be:
(a) W/91
(b) W/3
(c) W/100
(d) W/9
Ans: (c)
The weight of an object varies with altitude due to the change in gravitational force. The force of gravity decreases with the square of the distance from the center of the Earth.
The gravitational force (weight) at a height h from the surface of the Earth is given by:

where:
W' is the weight at height h,
W is the weight at the Earth's surface,
R is the radius of the Earth,
h is the height above the Earth's surface.
In this problem, the height h is given as nine times the radius of the Earth (h = 9R). Substituting h = 9R into the equation gives:

Simplifying this gives:
W' = W/100
Therefore, the weight of the body at that height will be 1/100th of its weight on the surface of the Earth.
The correct answer is Option C: W/100.
Q28: At a certain depth "d " below surface of earth, value of acceleration due to gravity becomes four times that of its value at a height 3 R above earth surface. Where R is Radius of earth (Take R = 6400 km). The depth d is equal to
(a) 5260 km
(b) 2560 km
(c) 640 km
(d) 4800 km
Ans: (d)
The acceleration due to gravity g at a distance d below the surface of the earth is given by:

where G is the gravitational constant and M is the mass of the Earth.
At a height 3R above the surface of the Earth, the acceleration due to gravity gh is given by:

Given, gd = 4gh, so we can write:



⇒ d = 4800 km
Q29: An object is allowed to fall from a height R above the earth, where R is the radius of earth. Its velocity when it strikes the earth's surface, ignoring air resistance, will be
(a) 
(b) 
(c) 
(d) 
Ans: (b)

⇒ Energy conservation

Q30: If the gravitational field in the space is given as . Taking the reference point to be at r = 2 cm with gravitational potential V = 10J / kg. Find the gravitational potential at r = 3 cm in SI unit (Given, that K = 6 Jcm / kg)
. Taking the reference point to be at r = 2 cm with gravitational potential V = 10J / kg. Find the gravitational potential at r = 3 cm in SI unit (Given, that K = 6 Jcm / kg)
(a) 9
(b) 11
(c) 10
(d) 12
Ans: (b)

Q31: The time period of a satellite of earth is 24 hours. If the separation between the earth and the satellite is decreased to one fourth of the previous value, then its new time period will become.
(a) 12 hours
(b) 3 hours
(c) 6 hours
(d) 4 hours
Ans: (b)

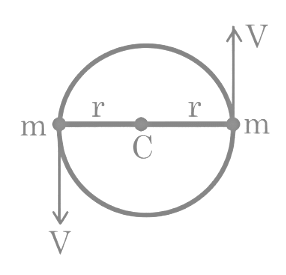
Q32: Two particles of equal mass 'm' move in a circle of radius 'r' under the action of their mutual gravitational attraction. The speed of each particle will be:
(a) 
(b) 
(c) 
(d) 
Ans: (a)



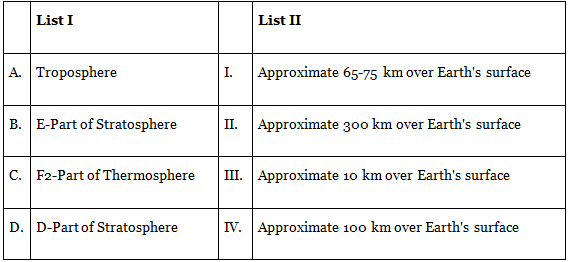
Q33: Match List I with List II
 Choose the correct answer from the options given below:
Choose the correct answer from the options given below:
(a) A-III, B-IV, C-II, D-I
(b) A-III, B-II, C-I, D-IV
(c) A-I, B-IV, C-III, D-II
(d) A-I, B-II, C-IV, D-III
Ans: (a)
→ 10 km over Earth's surface - Troposphere
→ 100 km over Earth's surface - E-part of stratosphere
→ 300 km over Earth's surface − F2 -part of thermosphere
→ 65-75 km over Earth's surface - D-part of stratosphere
Q34: Every planet revolves around the sun in an elliptical orbit :-
A. The force acting on a planet is inversely proportional to square of distance from sun.
B. Force acting on planet is inversely proportional to product of the masses of the planet and the sun.
C. The Centripetal force acting on the planet is directed away from the sun.
D. The square of time period of revolution of planet around sun is directly proportional to cube of semi-major axis of elliptical orbit.
Choose the correct answer from the options given below :
(a) C and D only
(b) B and C only
(c) A and D only
(d) A and C only
Ans: (c)
A. The force acting on a planet is inversely proportional to the square of the distance from the sun. This is known as the inverse square law and is described by Newton's law of gravitation.
B. Force acting on a planet is inversely proportional to the product of the masses of the planet and the sun. This is also described by Newton's law of gravitation, but it is not directly related to the planet's elliptical orbit.
C. The centripetal force acting on the planet is directed towards the sun, not away from it.
D. The square of the time period of revolution of a planet around the sun is directly proportional to the cube of the semi-major axis of the elliptical orbit. This is known as Kepler's third law.
Therefore, only A and D are correct.
Q35: A body of mass is taken from earth surface to the height h equal to twice the radius of earth (Re), the increase in potential energy will be:
(g = acceleration due to gravity on the surface of Earth)
(a) 
(b) 3 mg Re
(c) 
(d) 
Ans: (d)


Q36: Assume that the earth is a solid sphere of uniform density and a tunnel is dug along its diameter throughout the earth. It is found that when a particle is released in this tunnel, it executes a simple harmonic motion. The mass of the particle is 100 g. The time period of the motion of the particle will be (approximately) (Take g = 10 ms−2 , radius of earth = 6400 km)
(a) 12 hours
(b) 1 hour 24 minutes
(c) 24 hours
(d) 1 hour 40 minutes
Ans: (b)
Gravitational acceleration at a distance of r from centre of earth is given by

Where R is the radius of earth


= 5024 sec
= 1 hour 24 minutes (approx.)
Q37: Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: A pendulum clock when taken to Mount Everest becomes fast.
Reason R: The value of g (acceleration due to gravity) is less at Mount Everest than its value on the surface of earth.
In the light of the above statements, choose the most appropriate answer from the options given below (a) Both A and R are correct but R is NOT the correct explanation of A
(b) A is correct but R is not correct
(c) Both A and R are correct and R is the correct explanation of A
(d) A is not correct but R is correct
Ans: (d)
When we go on the Mount Everest the value of gravitational acceleration decreases 
Therefore, the time period of oscillation  increases and the pendulum clock becomes slow thus the assertion is wrong but reason is correct.
increases and the pendulum clock becomes slow thus the assertion is wrong but reason is correct.
Q38: If the distance of the earth from Sun is 1.5 × 106 km. Then the distance of an imaginary planet from Sun, if its period of revolution is 2.83 years is :
(a) 6 × 106 km
(b) 3 × 107 km
(c) 6 × 107 km
(d) 3 × 106 km
Ans: (d)
We can use Kepler's third law to solve this problem. Kepler's third law states that the square of the period of revolution of a planet around the Sun is proportional to the cube of its average distance from the Sun. Let T be the period of revolution of the imaginary planet in years, and let d be its average distance from the Sun in kilometers. We can use the following equation to solve for d:

where T1 and d1 are the period of revolution and an average distance of the Earth from the Sun, respectively, andT2 is the period of revolution of the imaginary planet.
Substituting the given values, we get:

Q39: Given below are two statements:
Statement I: Acceleration due to earth's gravity decreases as you go 'up' or 'down' from earth's surface.
Statement II: Acceleration due to earth's gravity is same at a height 'h' and depth 'd' from earth's surface, if h = d. In the light of above statements, choose the most appropriate answer from the options given below
(a) Statement I is correct but statement II is incorect
(b) Both Statement I and II are correct
(c) Statement I is incorrect but statement II is correct
(d) Both Statement I and Statement II are incorrect
Ans: (a)
Statement I is correct as acceleration due to Earth's gravity decreases as you move away from its surface either upward or downward. This is because the gravity of the Earth follows an inverse square law, which means that the gravitational force decreases as the square of the distance between two objects increases.
However, statement II is incorrect because acceleration due to Earth's gravity is not the same at a height and depth from Earth's surface, even if they are equal in magnitude. This is because the Earth is not a perfect sphere and has a non-uniform distribution of mass, which causes variations in the strength of gravity at different locations. Therefore, the acceleration due to Earth's gravity will be different at a certain height and depth, even if they are equal.
Q40: The weight of a body at the surface of earth is 18 N. The weight of the body at an altitude of 3200 km above the earth's surface is (given, radius of earth Re = 6400 km):
(a) 9.8 N
(b) 4.9 N
(c) 19.6 N
(d) 8 N
Ans: (d)
The weight of an object at a height h from the Earth's surface is given by:

where:
W' is the weight at height h,
W is the weight at the Earth's surface,
R is the radius of the Earth,
h is the height above the Earth's surface.
In this problem, the weight at the Earth's surface W is given as 18 N, the radius of the Earth R is given as 6400 km, and the height h is given as 3200 km. Substituting these values into the equation gives:

Therefore, the weight of the body at an altitude of 3200 km above the Earth's surface is 8 N.
[JEE Mains Numericals]
Q41: If the earth suddenly shrinks to  of its original volume with its mass remaining the same, the period of rotation of earth becomes
of its original volume with its mass remaining the same, the period of rotation of earth becomes  . The value of x is __________.
. The value of x is __________.
Ans: 16
 From the conservation of angular momentum, we have:
From the conservation of angular momentum, we have:

This simplifies to:

From this, we can derive the ratio of the initial and final angular velocities:

Since the angular velocity (ω) is inversely proportional to the period of rotation (T) 

We can express this ratio in terms of the variable (x):

Solving this equation for (x) gives:
x = 16
So, if the Earth suddenly shrinks to (1/64)th of its original volume with its mass remaining the same, the period of rotation of Earth becomes (24/16)h, or 1.5 hours. Therefore, the value of (x) is 16.
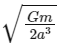
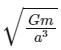
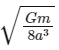
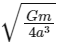
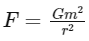
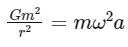
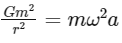
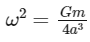
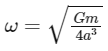
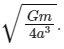
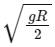
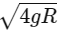
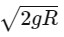
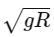
 By conservation of mechanical energy
By conservation of mechanical energy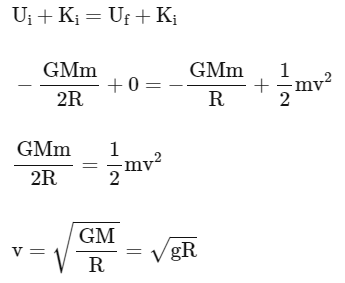
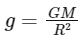
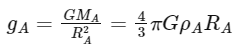
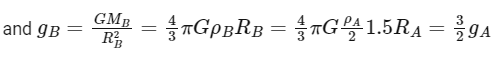
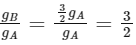
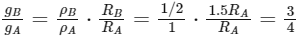
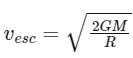
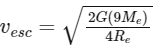
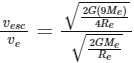
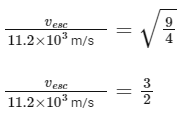
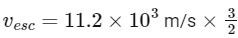
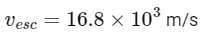
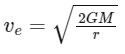
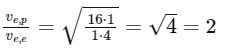
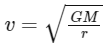
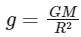
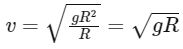
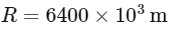
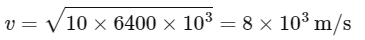
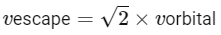

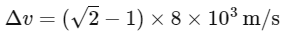

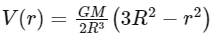
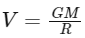
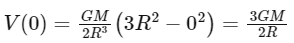
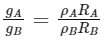

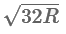
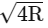
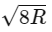
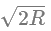
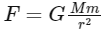
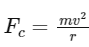

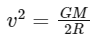
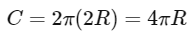
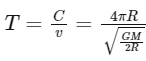
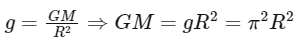
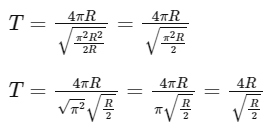
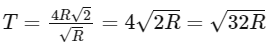
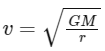
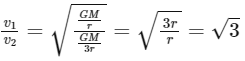
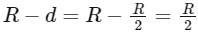 )
)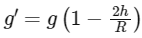
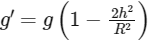
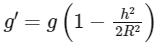
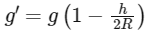
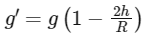
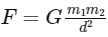
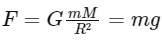
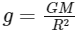 is the acceleration due to gravity at the Earth's surface.
is the acceleration due to gravity at the Earth's surface.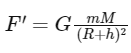
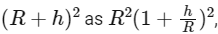 and because h << R , we can use the binomial approximation (1 + x)2 ≈ 1 + 2x for small x to get:
and because h << R , we can use the binomial approximation (1 + x)2 ≈ 1 + 2x for small x to get: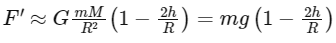
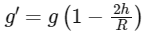
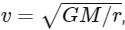 , where G is the gravitational constant, M is the mass of the Earth, and r is the distance from the center of the Earth to the satellite, then the orbital angular momentum (L) is:
, where G is the gravitational constant, M is the mass of the Earth, and r is the distance from the center of the Earth to the satellite, then the orbital angular momentum (L) is: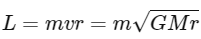
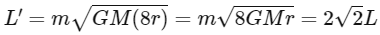
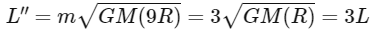
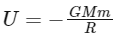
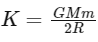
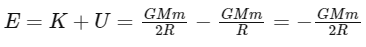
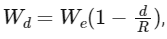
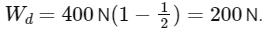
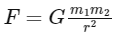
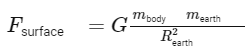
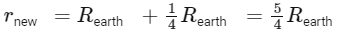
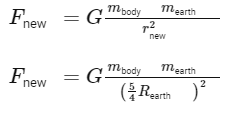
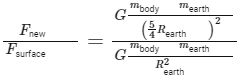
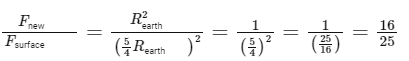
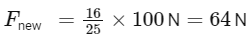
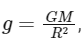 where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.
where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.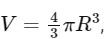 a doubling of the volume implies that the radius of the planet is
a doubling of the volume implies that the radius of the planet is 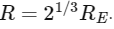
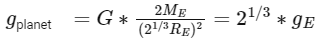
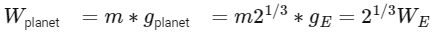
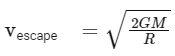
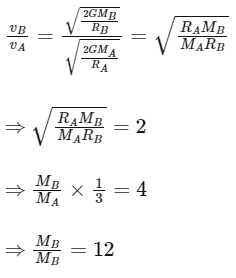
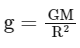
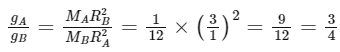
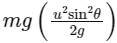
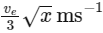 will be the minimum velocity required by a rocket to pull out of gravitational force of P , where ve is escape velocity on earth. The value of x is
will be the minimum velocity required by a rocket to pull out of gravitational force of P , where ve is escape velocity on earth. The value of x is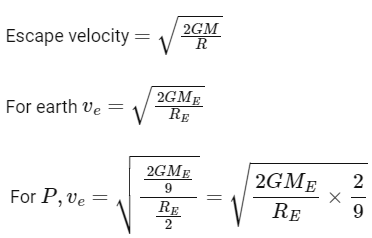
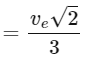
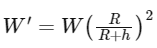
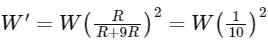
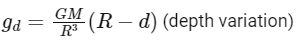
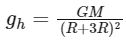
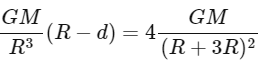
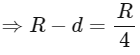
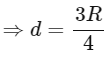
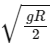
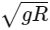
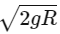
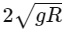
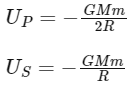
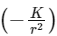 . Taking the reference point to be at r = 2 cm with gravitational potential V = 10J / kg. Find the gravitational potential at r = 3 cm in SI unit (Given, that K = 6 Jcm / kg)
. Taking the reference point to be at r = 2 cm with gravitational potential V = 10J / kg. Find the gravitational potential at r = 3 cm in SI unit (Given, that K = 6 Jcm / kg)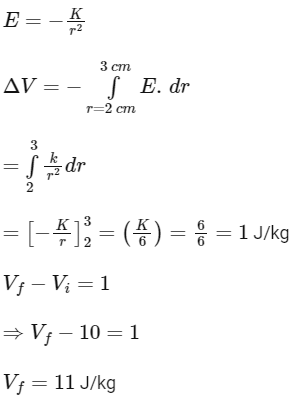
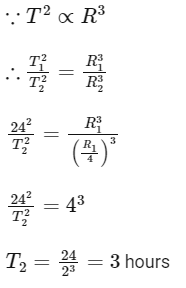
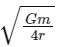
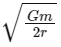
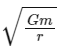
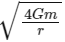
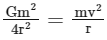
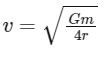
 Choose the correct answer from the options given below:
Choose the correct answer from the options given below: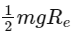
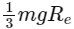
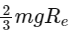

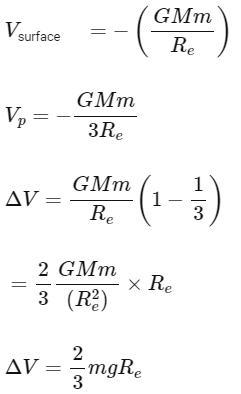
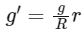
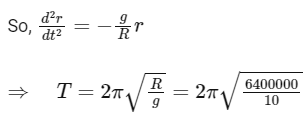
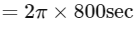
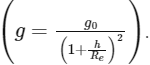
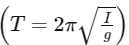 increases and the pendulum clock becomes slow thus the assertion is wrong but reason is correct.
increases and the pendulum clock becomes slow thus the assertion is wrong but reason is correct.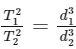
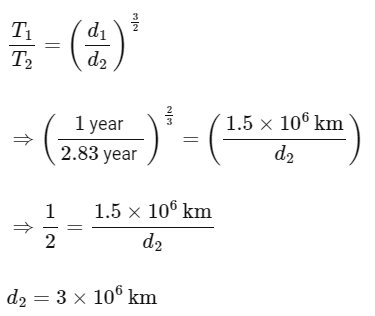
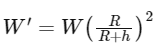
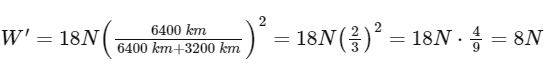
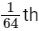 of its original volume with its mass remaining the same, the period of rotation of earth becomes
of its original volume with its mass remaining the same, the period of rotation of earth becomes 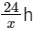 . The value of x is __________.
. The value of x is __________.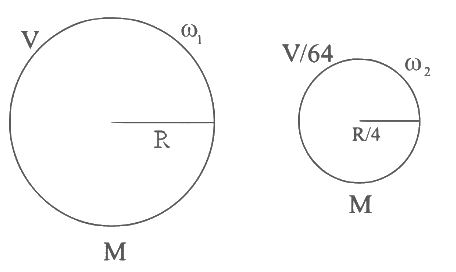 From the conservation of angular momentum, we have:
From the conservation of angular momentum, we have: