JEE Main Previous Year Questions (2023): Some Basic Concepts of Chemistry PDF Download

[JEE Main MCQs]

Q1: A metal chloride contains 55.0% of chlorine by weight. 100 mL vapours of the metal chloride at STP weigh 0.57 g. The molecular formula of the metal chloride is
(Given: Atomic mass of chlorine is 35.5u)
(a) MCl₂
(b) MCl₄
(c) MCl₃
(d) MCI
Ans: (a)
The weight percent of chlorine in the compound is given as 55.0%. This implies that the weight percent of the metal is 45.0%.
Now, we need to find the molar mass of the compound. At STP (standard temperature and pressure), 1 mole of any gas occupies 22.4 L. We know that 100 mL (or 0.1 L) of the metal chloride vapor weighs 0.57 g. Therefore, the molar mass of the compound (MClx) is:
MMCl_x = 0.57g/0.1 L × 22.4 L/mol = 127.68 g/mol
Given the weight percent of the metal and chlorine, we can find the molar mass of the metal (MM) using the equation: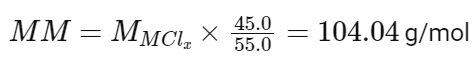

Subtracting the atomic mass of chlorine from the molar mass of the metal gives the molar mass of the metal:
MM - x.33.5 = 104.04 mol
Where 'x' is the number of chlorine atoms in the compound.
Solving this equation for 'x' gives: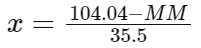
 
We find that 'x' is approximately 2. Therefore, the molecular formula of the compound is MCl₂. So, the correct answer is MCl₂.

Q2: A solution is prepared by adding 2 g of " X " to 1 mole of water. Mass percent of " X " in the solution is:
(a) 20%
(b) 10%
(c) 2%
(d) 5%
Ans: (b)
First, we need to calculate the mass of 1 mole of water (H₂O). The molecular weight of water is 18 g/mol, so 1 mole of water weighs 18 g.
The total mass of the solution is the mass of "X" plus the mass of water, which is 2 g + 18 g = 20 g.
We can calculate the mass percent of "X" in the solution with the following formula:
Mass percent of "X" = (mass of "X" total/mass of solution) × 100 %
Substitute the given values into the formula:
Mass percent of "X" = (2g/20g) × 100 % = 10 %
Therefore, Option B, 10 % , is the correct answer.

Q3: Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason B.
Assertion A: 3.1500 g of hydrated oxalic acid dissolved in water to make 250.0 mL solution will result in 0.1 M oxalic acid solution.
Reason: Molar mass of hydrated oxalic acid is 126 g mol⁻¹
In light of the above statements, choose the correct answer from the options given below.
(a) Both A and R are true but R is NOT the correct explanation of A
(b) A is true but R is false
(c) Both A and R are true and R is the correct explanation of A
(d) A is false but R is true
Ans: (c)

Firstly, let's calculate the molarity of the oxalic acid solution given in the Assertion (A).
The molarity (M) is defined as the number of moles of solute per liter of solution. The number of moles of solute is given by the mass of the solute divided by its molar mass.
So, the number of moles of hydrated oxalic acid is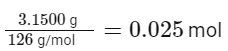
And the volume of the solution is 250.0 mL, or 0.250 L.
Therefore, the molarity of the solution is
This matches the molarity given in the Assertion (A), so the Assertion is true.
The Reason (R) gives the molar mass of hydrated oxalic acid as 126 g/mol, which was used in the calculation above. Therefore, the Reason is also true.
Moreover, the Reason (R) is the correct explanation of Assertion (A), as it provides the necessary information (the molar mass of hydrated oxalic acid) to calculate the molarity of the solution.
So, the correct option is C: Both A and R are true and R is the correct explanation of A.

Q4: Match List I with List II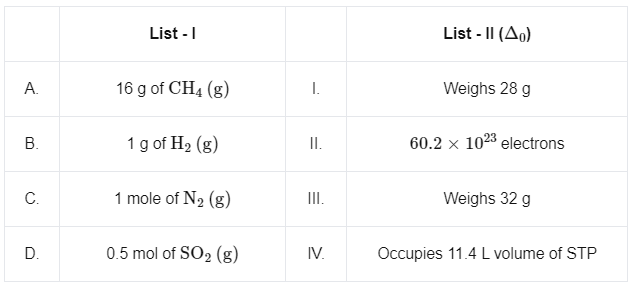

Choose the correct answer from the options given below:
(a) A-II, B-III, C-IV, D-I
(b) A-II, B-IV, C-I, D-III
(c) A-I, B-III, C-II, D-IV
(d) A-II, B-IV, C-III, D-I
Ans: (b)
A. 16 g of CH₄ (g)
The molar mass of CH₄ (Methane) is 16 g/mol. Therefore, 16 g of CH₄ is equivalent to 1 mole of CH₄ . Furthermore, each molecule of CH₄ has 10 electrons (6 from Carbon and 4 from Hydrogen). As a result, 1 mole of CH₄ (or 6.022 × 10²³ molecules of CH₄) would have 10 × 6.022 × 10²³ = 60.2 × 10²³ electrons. This matches with (II).
B. 1 g of H₂ (g)
The molar mass of H₂ (Hydrogen) is 2 g/mol. Therefore, 1 g of H₂ is equivalent to 0.5 moles of H₂. The volume that a given quantity of gas occupies is proportional to the number of moles of gas. At standard temperature and pressure (STP), 1 mole of any ideal gas occupies 22.4 liters. Therefore, 0.5 moles of gas would occupy 0.5 × 22.4 = 11.2 liters. The closest match is (IV) with 11.4 liters (the small discrepancy may be due to rounding or slightly different conditions than STP).
C. 1 mole of N₂ (g)
The molar mass of N₂ (Nitrogen) is 28 g/mol. Therefore, 1 mole of N₂ weighs 28 g. This matches with (I).
D. 0.5 mol of SO₂ (g)
The molar mass of SO₂ (Sulfur Dioxide) is 64 g/mol.
Therefore, 0.5 moles of SO₂ weigh 0.5 × 64 = 32 g. This matches with (III).
Thus, the correct matches are: A - II B - IV C - I D - III

Q5: Number of molecules & moles in 2.8375 litre of O₂ in STP
(a) 1.505 × 10²³ & 0.250
(b) 7.625 × 10²³ and 0.250
(c) 7.625 × 10²² and 0.126
(d) 7.527 × 10²² and 0.125
Ans: (d)
At STP, one mole of any gas occupies 22.4 liters. Therefore, 2.8375 liters of oxygen gas at STP is equal to 0.125 moles. The number of molecules of oxygen gas in 0.125 moles is calculated by multiplying the number of moles by Avogadro's number, which is 6.022 x 10²³ molecules/mol. This gives us a total of 7.527 x 10²² molecules of oxygen gas in 2.8375 liters at STP.
Here is the calculation:
Number of moles of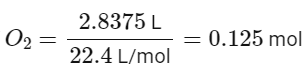
Number of molecules of O₂ = 0.125 mol x 6.022 x 10²³ molecules/mol = 7.527 x 10²² molecules.

Q6: Which of the following have same number of significant figures?
(a) 0.00253
(b) 1.0003
(c) 15.0
(d) 163
Choose the correct answer from the options given below
(a) A, C and D only
(b) B and C only
(c) A, B and C only
(d) C and D only
Ans: (a)
Significant figures are the digits in a number that carry meaningful information about its precision. In other words, they are the numbers that are known with certainty.
Here is how we calculate significant figures for each number:
A. 0.00253: There are 3 significant figures here (253). Leading zeroes do not count as significant figures.
B. 1.0003: There are 5 significant figures here. All non-zero digits are significant, and zeroes between non-zero digits or at the end of the number and after the decimal point are significant.
C. 15.0: There are 3 significant figures here. The zero after the decimal point counts as it indicates the precision of the measurement.
D. 163: There are 3 significant figures here. All non-zero digits are significant.
So, comparing these, we see that options A (0.00253), C (15.0), and D (163) each have 3 significant figures.

Q7: The volume of 0.02 M aqueous HBr required to neutralize 10.0 mL of 0.01 M aqueous Ba (OH)₂ is (Assume complete neutralization)
(a) 7.5 mL
(b) 5.0 mL
(c) 10.0 mL
(d) 2.5 mL
Ans: (c)
The reaction between HBr and Ba(OH)₂ is a neutralization reaction where one Ba(OH)₂ reacts with two HBr to form BaBr₂ and 2H₂O:
Ba(OH)₂ + 2HBr → BaBr₂ + 2H₂O
We can use the stoichiometry of the reaction to find the volume of HBr required.
The number of moles of Ba(OH)2 is given by its molarity times the volume in liters: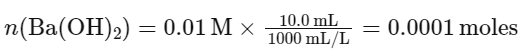

From the balanced equation, we can see that the reaction requires 2 moles of HBr for each mole of Ba(OH)₂: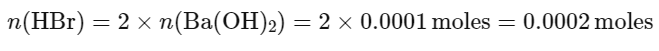
 
Then, we find the volume of the HBr solution by dividing the number of moles by the molarity:
 
Therefore, the volume of the 0.02 M HBr solution required to neutralize the Ba (OH)₂ solution is 10.0 mL.

Q8: When a hydrocarbon A undergoes complete combustion it requires 11 equivalents of oxygen and produces 4 equivalents of water. What is the molecular formula of A ?
(a) C₉H₈
(b) C₁₁H₄
(c) C₅H₈
(d) C₁₁H₈
Ans: (a)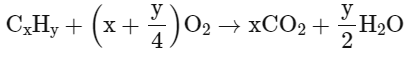

y/2 = 4 ⇒ y = 8
x + 8 4 = 11
⇒ x = 9
∴ Hydrocarbon will be = C₉H₈

Q9: 1 L, 0.02 M solution of [Co(NH₃)₅SO₄]Br is mixed with 1L, 0.02 M solution of [Co(NH₃)₅Br]SO₄. The resulting solution is divided into two equal parts (X) and treated with excess AgNO₃ solution and BaCl₂ solution respectively as shown below.
1 L Solution (X) + AgNO₃ solution (excess) → Y
1 L Solution (X) + BaCl₂ solution (excess) → Z
The number of moles of Y and Z respectively are
(a) 0.01, 0.01
(b) 0.01, 0.02
(c) 0.02, 0.01
(d) 0.02, 0.02 
Ans: (a)
On mixing both [Co(NH₃)₅SO₄]Br and [Co(NH₃)₅Br]SO₄ becomes 0.01 molar.
∴ Moles of y and z formed will also be 0.01 both.

Q10: When a hydrocarbon A undergoes combustion in the presence of air, it requires 9.5 equivalents of oxygen and produces 3 equivalents of water. What is the molecular formula of A?
(a) C₉H₆
(b) C₆H₆
(c) C₈H₆
(d) C₉H₉ 
Ans: (c)

y/2  = 3
y = 6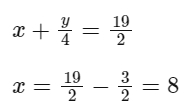

So, the formula is C₈H₆.

Q11: What is the mass ratio of ethylene glycol (C₂H₆O₂, molar mass = 62 g/mol) required for making 500 g of 0.25 molal aqueous solution and 250 mL of 0.25 molar aqueous solution?
(a) 1 : 2
(b) 1 : 1
(c) 2 : 1
(d) 3 : 1
Ans: (c)
For 500 g of 0.25 molal aqueous solution,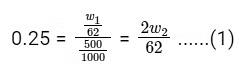

For 250 mL of 0.25 molar aqueous solution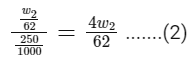

Dividing equation (1) by (2), we get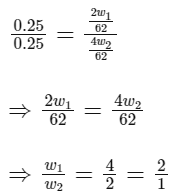

Note:
(1) Molality of solution is defined as number of moles of solute present per kg of solvent.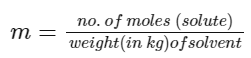

(2) Molarity of solution is defined as number of moles of solute present per litre of solution.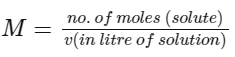


Q12: '25 volume' hydrogen peroxide means
(a) 1 L marketed solution contains 75 g of H₂O₂.
(b) 1 L marketed solution contains 250 g of H₂O₂.
(c) 1 L marketed solution contains 25 g of H₂O₂.
(d) 100 mL marketed solution contains 25 g of H₂O₂.
Ans: (a)
Molarity of H₂O₂ soln =  volume strength/11.2
= 25/11.2 = 2.23 M
∴ amount of H₂O₂ in one litre = 2.23 × 34 = 75 gm

[JEE Main Numericals]

Q13: The volume (in mL ) of 0.1 M AgNO₃ required for complete precipitation of chloride ions present in 20 mL of 0.01 M solution of [Cr(H₂O)₅Cl]Cl₂ as silver chloride is __________.
Ans: 4
The given solution contains a complex ion (Cr(H₂O)5Cl)Cl₂ which contains one chloride ion per complex. Therefore, when this complex is treated with silver nitrate, each mole of the complex will consume 2 moles of silver nitrate to form two moles of silver chloride.
The first step is to write the balanced chemical equation for the reaction between the complex and silver nitrate, as follows:
(Cr(H₂O)₅Cl)Cl₂ + 2AgNO₃ ⟶ (Cr(H₂O)₅Cl ) + 2AgCl + 2NO₃ ⁻ 
From the equation, we can see that 1 mole of the complex consumes 2 moles of silver nitrate to form 2 moles of silver chloride. Therefore, the number of millimoles of chloride ions present in the given solution can be calculated as:
Millimoles of Cl⁻ ions = concentration × volume = 0.01 M × 2 × 10 mL = 0.2 mmol
To calculate the volume of 0.1 M silver nitrate required, we can use the formula:
Millimoles of silver nitrate required = Millimoles of chloride ions × 2 = 0.4 mmol
We can then use the formula:
Volume of silver nitrate solution = Millimoles of silver nitrate required/Molarity of silver nitrate solution
Substituting the values, we get
Volume of silver nitrate solution = 0.4 mmol/0.1 M = 4 mL
Therefore, the volume of 0.1 M silver nitrate required for complete precipitation of chloride ions present in 20 mL of 0.01 M [Cr(H₂O)5Cl]Cl₂ solution as silver chloride is 4 mL .

Q14: 1g of a carbonate (M₂CO₃) on treatment with excess HCl produces 0.01 mol of CO₂ . The molar mass of M₂CO₃ is g mol^-1. (Nearest integer)
Ans: 100
When the carbonate reacts with HCl, it produces CO₂, as shown in the following balanced equation:
M₂CO₃ + 2HCl → 2MCl + H₂O + CO₂ 
From the problem, we know that 1 g of the carbonate produces 0.01 mol of CO₂.
To determine the molar mass of the carbonate, we can use the stoichiometry of the reaction:
1 mol of M₂CO₃ produces 1 mol of CO₂.
So, 0.01 mol of CO2 corresponds to 0.01 mol of M₂ CO₃.
Now, we can find the molar mass of M₂CO₃ :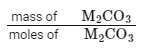
= molar mass of M₂CO₃ g
1g/0.01 mol = 100 g mol⁻¹
So, the molar mass of M₂CO₃ is approximately 100 g/mol.

Q15: An organic compound gives 0.220 g of CO₂ and 0.126 g of H₂O on complete combustion. If the % of carbon is 24 then the % hydrogen is____ x 10^-1. (Nearest integer)
Ans: 56
To find the percentage of hydrogen in the compound, we first need to determine the ratio of moles of carbon and hydrogen in the products.
The moles of CO₂ produced can be calculated by dividing the mass of CO₂ produced by its molar mass (44.01 g/mol):
moles of CO₂ = 0.220 g/44.01 g / mol = 0.005 mol
Since each mole of CO₂ contains one mole of carbon, there are 0.005 moles of carbon in the compound.
Now, let's calculate the moles of H₂O produced:
moles of H₂O = 0.126 g/18.02 g/mol = 0.007 mol
Since each mole of H₂O contains two moles of hydrogen, there are 0.014 moles of hydrogen in the compound.
Now, let's find the masses of carbon and hydrogen in the compound:
Mass of carbon = moles of carbon × molar mass of carbon  
Mass of carbon = 0.005 mol × 12.01 g / mol = 0.060 g
Mass of hydrogen = moles of hydrogen × molar mass of hydrogen
Mass of hydrogen = 0.014 mol × 1.008 g / mol = 0.014 g
Now, we are given that the percentage of carbon is 24%. Let's find the total mass of the compound:
The total mass of compound = Mass of carbon/% of carbon = 0.060 g/0.24 = 0.250 g
Finally, let's find the percentage of hydrogen:

So, the percentage of hydrogen is 5.6% or 56 × 10^-1.

Q16: 20 mL of calcium hydroxide was consumed when it was reacted with 10 mL of unknown solution of H₂SO₄. Also 20 mL standard solution of 0.5 M HCI containing 2 drops of phenolphthalein was titrated with calcium hydroxide the mixture showed pink colour when burette displayed the value of 35.5 mL whereas the burette showed 25.5 mL initially. The concentration of H₂SO₄ is_____M (Nearest integer)
Ans: 1
Reaction with HCI
Ca(OH)₂ + 2HCl → CaCl₂ + 2H₂O
Volume of Ca(OH)₂ = 10 ml
Volume of HCl = 20 ml
Concentration of HCl = 0.5 M.
No. of milli moles of HCl = 10
No. of milli moles of Ca(OH)₂ = 5.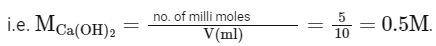

Reaction with H₂SO₄: .
Ca(OH)₂ + H₂SO₄ → CaSO₄ + 2H₂O .
No. of milli moles of Ca(OH)₂ = 20 × 0.5 = 10
i.e. no. of milli moles of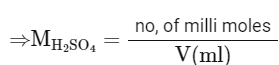

= 10/10
= 1 M
So, the concentration of H₂SO₄ is 1 M.

Q17: The volume of hydrogen liberated at STP by treating 2.4 g of magnesium with excess of hydrochloric acid is _________ × 10⁻² L
Given: Molar volume of gas is 22.4 L at STP.
Molar mass of magnesium is 24 g mol-1
Ans: 224
The reaction between magnesium and hydrochloric acid is as follows :
`Mg(s) + 2HCl(aq) → MgCl2(aq) + H2(g)`
From the equation, we see that 1 mole of magnesium (Mg) produces 1 mole of hydrogen gas (H2).
The molar mass of magnesium (Mg) is given as 24 g/mol. Therefore, 2.4 g of magnesium would correspond to (2.4 g)/(24 g/mol) = 0.1 mol of Mg.
Since 1 mole of Mg produces 1 mole of H2, 0.1 mol of Mg would produce 0.1 mol of H2.
At STP (Standard Temperature and Pressure), the molar volume of a gas is 22.4 L/mol.
Therefore, the volume of 0.1 mol of H2 would be (0.1 mol)*(22.4 L/mol) = 2.24 L.
So, the volume of hydrogen liberated at STP by treating 2.4 g of magnesium with excess of hydrochloric acid is 2.24 L.
In the terms of the question where the volume is expressed as ______ × 10-2 L, we convert 2.24 L into the desired form, i.e., 2.24 L = 2.24 × 10² × 10^-2 L, so the answer is 224 × 10^-2 L.

Q18: A solution of sugar is obtained by mixing 200 g of its 25 % solution and 500 g of its 40 % solution (both by mass). The mass percentage of the resulting sugar solution is ___________ (Nearest integer)
Ans: 36
Let's first calculate the amount of sugar in each of the solutions :
In the 25% sugar solution, the amount of sugar is 25% of 200 g, which equals 50 g.
In the 40% sugar solution, the amount of sugar is 40% of 500 g, which equals 200 g.
Now, let's mix these two solutions together:
The total amount of sugar in the combined solution is 50 g (from the 25% solution) + 200 g (from the 40% solution) = 250 g.
The total weight of the combined solution is 200 g (of the 25% solution) + 500 g (of the 40% solution) = 700 g.
Therefore, the mass percentage of sugar in the combined solution is = 250/700 × 100 = 35.71%
Rounding to the nearest integer gives 36%. So, the mass percentage of the resulting sugar solution is 36%.

Q19: 0.5 g of an organic compound ( X ) with 60 % carbon will produce __________ × 10⁻¹ g of CO₂ on complete combustion.
Ans: 11
Mass of Carbon = 12
Molar Mass of CO₂ = 12 + (16 × 2) = 44
Mass of Compound = 0.5g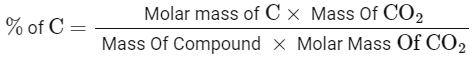


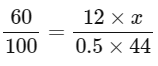
1.1 = x
x = 11 x 10^-1

Q20: If 5 moles of BaCl₂ is mixed with 2 moles of Na₃PO₄, the maximum number of moles of Ba₃(PO₄)₂ formed is___. (Nearest integer)
Ans: 1
Given the balanced chemical equation: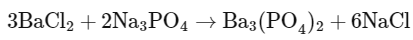
 
We can see that 3 moles of BaCl₂ react with 2 moles of Na₃PO₄ to produce 1 mole of Ba₃(PO₄)₂.
Given that you have 5 moles of BaCl₂ and 2 moles of Na₃PO₄ , let's calculate the maximum number of moles of Ba₃(PO₄)₂ that can be formed:
From BaCl₂, using the molar ratio from the balanced equation: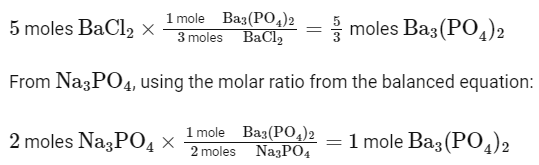

The limiting reactant is Na₃PO₄ because it produces 1 mole of Ba₃(PO₄)₂ , which is less than the 5/3 moles produced by BaCl₂. Therefore, the maximum number of moles of Ba₃(PO₄)₂ formed is 1 mole. Rounding to the nearest integer, the answer is 1.

Q21: The molality of a 10% (v/v) solution of di-bromine solution in CCl₄ (carbon tetrachloride) is 'x'. x = ________ × 10^–2 M. (Nearest integer)
[Given: molar mass of Br₂ = 160 g mol^–1
atomic mass of C = 12 g mol^–1
atomic mass of Cl = 35.5 g mol^–1
density of dibromine = 3.2 g/cm^–3
density of CCl₄ = 1.6 g cm^–3]
Ans: 139
Mass of 10 mL of Br₂ = 10 × 3.2 = 32 gm
Mass of 90 mL^LCCl₄ = 90 × 1.6 = 144 gm
Molality of Br₂ solution in CCl₄

= 1.39 M
= 139 x 10^-2

Q22: The density of 3 M solution of NaCl is 1.0 g mL^-1. The molality of the solution is ________ × 10^-2 m. (Nearest integer).
Given: Molar mass of Na and Cl is 23 and 35.5 g mol^-1 respectively
Ans: 364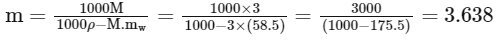

= 363.8 × 10⁻² 
Nearest integer = 364

Q23: Assume carbon burns according to the following equation:
2C_(s) + O_2(g) → 2CO_(g) 
when 12 g carbon is burnt in 48 g of oxygen, the volume of carbon monoxide produced is ___________ × 10⁻¹ L at STP [nearest integer]
[Given: Assume CO as ideal gas, Mass of C is 12 g mol⁻¹, Mass of O is 16 g mol⁻¹ and molar volume of an ideal gas at STP is 22.7 L mol⁻¹]
Ans: 227
2C(s) + O2(g) → 2CO(g)
1mol 1.5 mol
Limiting reagent is carbon. One mole carbon produces one mole CO. Hence, volume at STP is 227 x 10^-1 liter.

Q24: A sample of a metal oxide has formula M_0.83O_1.00. The metal M can exist in two oxidation states +2 and +3.
In the sample of M_0.83O_1.00, the percentage of metal ions existing in +2 oxidation state is _____ % (nearest integer)
Ans: 59
Let, metal M present x and (0.83 - x) in oxidation states + 2 and + 3 respectively.
2x + 3(0.83 − x) = 2
x = 0.49
%M² + = 0.49/0.83 × 100
= 59 %

Q25: Zinc reacts with hydrochloric acid to give hydrogen and zinc chloride. The volume of hydrogen gas produced at STP from the reaction of 11.5 g of zinc with excess HCl is __________ L (Nearest integer) 
(Given: Molar mass of Zn is 65.4 g mol⁻¹ and Molar volume of H₂ at STP = 22.7 L)
Ans: 4
Zn + 2HCl → ZnCl₂ + H₂ ↑
Moles of Zn used = 11.5/65.4 = Moles of H₂ evolved
Volume of H₂ = 11.5/65.4 x 22.7 L = 3.99 L

Q26: On complete combustion, 0.492 g of an organic compound gave 0.792 g of CO₂. The % of carbon in the organic compound is ___________ (Nearest integer)
Ans: 44
Weight of C in 0.792 gm CO₂
= 12/44 × 0.792 = 0.216
% of C in compound = 0.216/0.492 × 100
= 43.90 %

Q27: The strength of 50 volume solution of hydrogen peroxide is ______ g / L (Nearest integer).
Given: Molar mass of H₂O₂ is 34 g mol⁻¹ 
Molar volume of gas at STP = 22.7 L
Ans: 150
H₂O₂ ⟶ H₂O + 1/2 O₂ 
50/22.7
∴ Moles of H₂O₂ in solution = 50/22.7 × 2
∴ Strength = 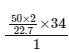= 149.78 ≈ 150

Q28: Some amount of dichloromethane (CH₂Cl₂) is added to 671.141 mL of chloroform (CHCl₃) to prepare 2.6 x 10^-3 M solution of CH₂Cl₂ DCM. The concentration of DCM is ______ ppm (by mass).
Given:
Atomic mass : C = 12;
H : 1;
Cl = 35.5
density of CHCl₃ = 1.49 g cm^-3
Ans: 148
Mass of CHCl₃ = 671.141 × 1.49 = 1000 gm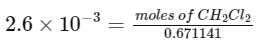

⇒ moles of CH₂Cl₂ = 1.74496 × 10⁻³ 
mass of CH₂Cl₂ = 148.32 × 10⁻³ gm
Composition of CH₂Cl₂ =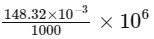  
= 148.32 ppm
≈ 148

Q29: The volume of HCl, containing 73 g L⁻¹, required to completely neutralise NaOH obtained by reacting 0.69 g of metallic sodium with water, is __________ mL. (Nearest Integer)
(Given: molar masses of Na, Cl, O, H, are 23, 35.5, 16 and 1 g mol⁻¹ respectively.)
Ans: 15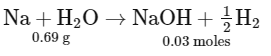

= 0.03 moles
∴ 0.03 = 2 × V
V = 0.03/2 L
= 15 mL

Q30: When 0.01 mol of an organic compound containing 60% carbon was burnt completely, 4.4 g of CO₂ was produced. The molar mass of compound is _____________ g mol⁻¹ (Nearest integer).
Ans: 200
Number of moles of CO₂ = 4.4/44 = 0.1
∴ Number of moles of C in 1 mole of compound = 10
∴ 120 = 60/100 × (x) [where x is molar mass of OC]
Molar mass = 200 g mol⁻¹

Q31: Number of hydrogen atoms per molecule of a hydrocarbon A having 85.8% carbon is __________
(Given: Molar mass of A = 84 g mol⁻¹)
Ans: 1
Molar mass of a hydrocarbon (A) = 84 g / mol
Mass of carbon in 1 mol of (A) = 85.8/100 × 84
= 72 gm
Mass of hydrogen in 1 mol of (A) = 12 gm
∴ Number of H -atoms in a molecule of (A) = 12 .

Q32: In sulphur estimation, 0.471 g of an organic compound gave 1.4439 g of barium sulphate. The percentage of sulphur in the compound is ____________ (Nearest Integer)
(Given : Atomic mass Ba: 137 u, S: 32 u, O: 16 u)
Ans: 42


= 42.10

Q33: The number of units, which are used to express concentration of solutions from the following is _________
Mass percent, Mole, Mole fraction, Molarity, ppm, Molality
Ans: 5
Mass percent, mole fraction, molarity, ppm & molality is used to express concentration. So, the number of units = 5

Q34: When Fe_0.93O is heated in presence of oxygen, it converts to Fe₂O₃. The number of correct statement/s from the following is _______.
A. The equivalent weight of Fe_0.93O is Molecular weight/0.79.
B. The number of moles of Fe²⁺ and Fe³⁺ in 1 mole of Fe_0.93O is 0.79 and 0.14 respectively.
C. Fe_0.93O is metal deficient with lattice comprising of cubic closed packed arrangement of O^2– ions.
D. The % composition of Fe²⁺ and Fe³⁺ in Fe_0.93O is 85% and 15% respectively.
Ans: 4
Let the number of Fe²⁺ ions be x and number of Fe³⁺ ions be 0.93 − x.
According to the charge neutrality,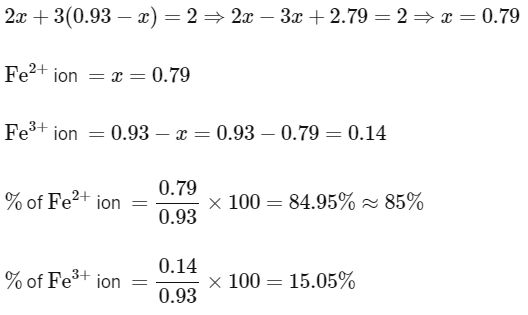

As it is a metal deficiency defect,
so, 1 mol of Fe_0.93O contains 1 mol of oxide ions and 0.93 mol of iron ions as Fe²⁺ and Fe³⁺.
So, moles of Fe²⁺ = 0.79
and moles of Fe³⁺ = 0.14
The equivalent weight = Molecular weight/n -factor
Fe²⁺ → Fe³⁺ + e⁻ 
For one Fe²⁺, n-factor = 1
∴ For 0.79 Fe²⁺, n -factor = 0.79
Out of 0.93 mol, there are 0.79 mol Fe²⁺ ions are present

Q35: 5 g of NaOH was dissolved in deionized water to prepare a 450 mL stock solution. What volume (in mL) of this solution would be required to prepare 500 mL of 0.1 M solution? _____________
Given: Molar Mass of Na, O and H is 23, 16 and 1 g mol⁻¹ respectively.
Ans: 180
Molarity of solution = 5/(40) (1000)/(450)
⇒ M × V = 500 × .1
⇒ 5/40 × 1000/450 × V = 500 × 0.1
V = 180 mL