JEE Main Previous Year Questions (2025): Permutations and Combinations | Chapter-wise Tests for JEE Main & Advanced PDF Download
[JEE Mains MCQs]
Q1: Let P1, P2, ......, P15 be 15 points on a circle. The number of distinct triangles formed by points Pi, Pj, Pk such that i +j + k ≠ 15, is:
(a) 12
(b) 419
(c) 443
(d) 455
Ans: (c)
Total number of triangles = 15C3
i + j + k = 15 (Given) Number of possible triangles using the vertices Pi, Pj, Pk such that i + j + k ≠ 15 is equal to 15C3 − 12 = 443
Number of possible triangles using the vertices Pi, Pj, Pk such that i + j + k ≠ 15 is equal to 15C3 − 12 = 443
Q2: If nPr = nPr+1 and nCr = nCr−1, then the value of r is equal to:
(a) 1
(b) 4
(c) 2
(d) 3
Ans: (c)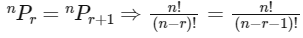
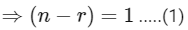
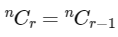
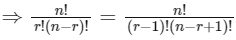
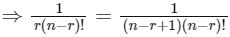
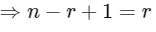
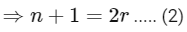
From (1) and (2), 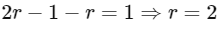
Q3: The sum of all the 4-digit distinct numbers that can be formed with the digits 1, 2, 2 and 3 is :
(a) 26664
(b) 122664
(c) 122234
(d) 22264
Ans: (a)
Total possible numbers using 1, 2, 2 and 3 is
= 4!/2! = 12
When unit place is 1, the total possible numbers using remaining 2, 2 and 3 are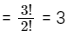
When unit place is 2, the total possible numbers using remaining 1, 2 and 3 are = 3! = 6
When unit place is 3, the total possible numbers using remaining 1, 2 and 2 are = 3!/2! = 3
∴ Sum of unit places of all (3 + 6 + 3) 12 numbers is
= (1 × 3 + 2 × 6 + 3 × 3)
Similarly,
When 10th place is 1, the total possible numbers using remaining 2, 2 and 3 are
= 3!/2! = 3
When 10th place is 2, the total possible numbers using remaining 1, 2 and 3 are
= 3! = 6
When 10th place is 3, the total possible numbers using remaining 1, 2 and 2 are
= 3!/2! = 3
∴ Sum of 10th places of all (3 + 6 + 3) 12 numbers is
= (1 × 3 + 2 × 6 + 3 × 3) × 10
Similarly,
Sum of 100th places of all (3 + 6 + 3) 12 numbers is
= (1 × 3 + 2 × 6 + 3 × 3) × 100
and Sum of 1000th places of all (3 + 6 + 3) 12 numbers is
= ( 1×3 + 2×6 + 3×3) × 1000
∴ Total sum = (1×3 + 2×6 + 3×3) + (1×3 + 2×6 + 3×3) × 10 + (1×3 + 2×6 + 3×3) × 100 + (1×3 + 2×6 + 3×3) × 1000
= (3 + 12 + 9) (1 + 10 + 100 + 1000) = 1111 × 24 = 26664
Q4: If the sides AB, BC and CA of a triangle ABC have 3, 5 and 6 interior points respectively, then the total number of triangles that can be constructed using these points as vertices, is equal to :
(a) 240
(b) 360
(c) 333
(d) 364
Ans: (c) Total number of triangles
Total number of triangles
= 14C3 − 3C3 − 5C3 − 6C3
= 364 – 31 = 333
Q5: Team 'A' consists of 7 boys and n girls and Team 'B' has 4 boys and 6 girls. If a total of 52 single matches can be arranged between these two teams when a boy plays against a boy and a girl plays against a girl, then n is equal to:
(a) 5
(b) 2
(c) 4
(d) 6
Ans: (c)
Total matches between boys of both team = 7C1 × 4C1 = 28
Total matches between girls of both team = nC1 6C1 = 6n
Now, 28 + 6n = 52
⇒ n = 4
Q6: Consider a rectangle ABCD having 5, 7, 6, 9 points in the interior of the line segments AB, CD, BC, DA respectively. Let α be the number of triangles having these points from different sides as vertices and β be the number of quadrilaterals having these points from different sides as vertices. Then (β − α) is equal to:
(a) 717
(b) 795
(c) 1890
(d) 1173
Ans: (a)
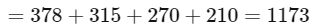
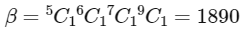
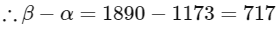
Q7: A natural number has prime factorization given by n = 2x3y5z, where y and z are such that y + z = 5 and y−1 + z−1 = 5/6 , y > z. Then the number of odd divisions of n, including 1, is:
(a) 11
(b) 6
(c) 12
(d) 6x
Ans: (c)
y + z = 5 ____ (1)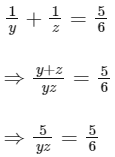
⇒ yz = 6
Also, (y − z)2 = (y + z)2 − 4yz
⇒ (y − z)2 = (y + z)2 − 4yz
⇒ (y − z)2 = 25 − 4(6) = 1
⇒ y − z = 1 ..... (2)
from (1) and (2), y = 3 and z = 2
for calculating odd divisor of p = 2x . 3y . 5z
x must be zero
P = 20 . 33 . 52
⇒ Total possible cases = (3050 + 3150 + 3250 + 3350 + .... + 3352)
∴ Total odd divisors must be (3 + 1) ( 2 + 1) = 12
Q8: The number of seven digit integers with sum of the digits equal to 10 and formed by using the digits 1, 2 and 3 only is:
(a) 35
(b) 42
(c) 82
(d) 77
Ans: (d)
(I) First possibility is 1, 1, 1, 1, 1, 2, 3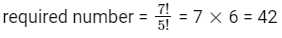
(II) Second possibility is 1, 1, 1, 1, 2, 2, 2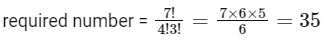
Total = 42 + 35 = 77
Q9: The total number of positive integral solutions (x, y, z) such that xyz = 24 is :
(a) 36
(b) 24
(c) 45
(d) 30
Ans: (d)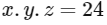
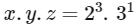
Three 2 has to be distributed among x, y and z Each may receive none, one or two
∴ Number of ways = 3+3−1C3−1 = 5C2 ways
Similarly one 3 has to be distributed among x, y and z
∴ Number of ways = 1+3−1C3−1 = 3C2 ways
Total ways = 5C2 . 3C2 = 30
Q10: A scientific committee is to be formed from 6 Indians and 8 foreigners, which includes at least 2 Indians and double the number of foreigners as Indians. Then the number of ways, the committee can be formed, is:
(a) 1050
(b) 575
(c) 560
(d) 1625
Ans: (d)
Given,
Number of Indians = 6
Number of foreigners = 8
Committee of at least 2 Indians and double number of foreigners is to be formed. Hence, the required cases are
(2I, 4F) + (3I, 6F) + (4I, 8F)
= 6C2 × 8C4 + 6C3 × 8C6 + 6C4 × 8C8
= (15 × 70) + (20 × 28) + (15 × 1)
= 1050 + 560 + 15 = 1625
[JEE Mains Numericals]
Q11: All the arrangements, with or without meaning, of the word FARMER are written excluding any word that has two R appearing together. The arrangements are listed serially in the alphabetic order as in the English dictionary. Then the serial number of the word FARMER in this list is ___________.
Ans: 77
First find all possible words and then subtract words from each case that have both R together.
FARMER (6)
A, E, F, M, R, R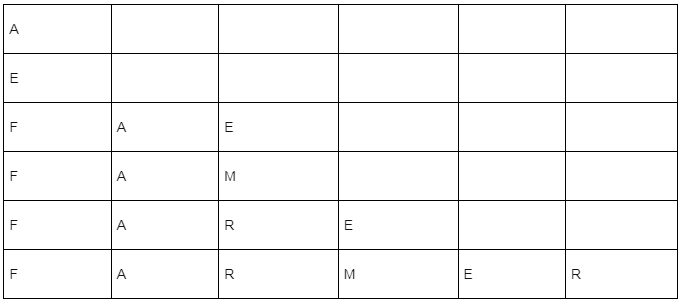

Q12: The number of six letter words (with or without meaning), formed using all the letters of the word 'VOWELS', so that all the consonants never come together, is ___________.
Ans: 576
Total possible words = 6! = 720
When 4 consonants are together (V, W, L, S)
such cases = 3! ⋅ 4! = 144
All consonants should not be together
= Total − All consonants together,
= 6! − 3! 4! = 576
Q13: Let S = {1, 2, 3, 4, 5, 6, 9}. Then the number of elements in the set T = {A ⊆ S : A ≠ ϕ and the sum of all the elements of A is not a multiple of 3} is _______________.
Ans:
3n type → 3, 6, 9 = P
3n − 1 type → 2, 5 = Q
3n − 2 type → 1, 4 = R
number of subset of S containing one element which are not divisible by 3 = 2C1 + 2C1 = 4
number of subset of S containing two numbers whose some is not divisible by 3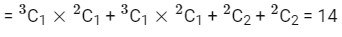
number of subsets containing 3 elements whose sum is not divisible by 3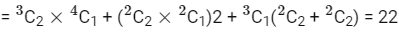
number of subsets containing 4 elements whose sum is not divisible by 3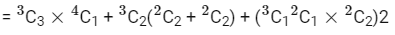
= 4 + 6 + 12 = 22
number of subsets of S containing 5 elements whose sum is not divisible by 3.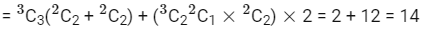
number of subsets of S containing 6 elements whose sum is not divisible by 3 = 4
⇒ Total subsets of Set A whose sum of digits is not divisible by 3 = 4 + 14 + 22 + 22 + 14 + 4 = 80.
Q14: A number is called a palindrome if it reads the same backward as well as forward. For example 285582 is a six digit palindrome. The number of six digit palindromes, which are divisible by 55, is ____________.
Ans: 100
5abba5
For divisible by 55 it shall be divisible by 11 and 5 both, for divisibility by 5 unit digit shall be 0 or 5 but as the number is six digit palindrome unit digit is 5.
A number is divisible by 11 if the difference between sum of the digits in the odd places and the sum of the digits in the even places is a multiple of 11 or zero.
Sum of the digits in the even place = a + b + 5
Sum of the digits in the odd places = a + b + 5
Difference between the two sums = (a + b + 5) - (a + b + 5) = 0
0 is divisible by 11.
Hence, 5abba5 is divisible by 11.
So, required number = 10 × 10 = 100
Q15: If 1P1 + 2. 2P2 + 3. 3P3 + . . . . + 15. 15P15 = qPr − s , 0 ≤ s ≤ 1 , then q+sCr−s is equal to ______________.
Ans: 136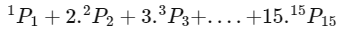
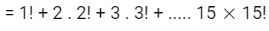
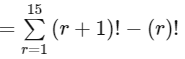
= 16! - 1
= 16P16 - 1
⇒ q = r = 16, s = 1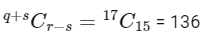
Q16: The number of three-digit even numbers, formed by the digits 0, 1, 3, 4, 6, 7 if the repetition of digits is not allowed, is ______________.
Ans: 52
(i) When '0' is at unit place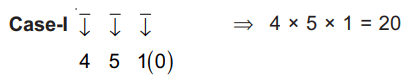
Number of numbers = 20
(ii) When 4 or 6 are at unit place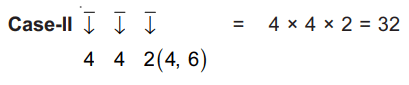
Number of numbers = 32
Total three digit even number = 20 + 32 = 52
Q17: Let n be a non-negative integer. Then the number of divisors of the form "4n + 1" of the number (10)10. (11)11. (13)13 is equal to __________.
Ans: 924
Now, power of 2 must be zero,
power of 5 can be anything,
power of 13 can be anything
But, power of 11 should be even.
So, required number of divisors is
1 × 11 × 14 × 6 = 924
Q18: There are 5 students in class 10, 6 students in class 11 and 8 students in class 12. If the number of ways, in which 10 students can be selected from them so as to include at least 2 students from each class and at most 5 students from the total 11 students of class 10 and 11 is 100 k, then k is equal to _____________.
Ans: 238

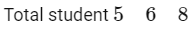

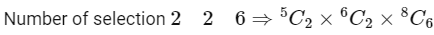

⇒ Total number of ways = 23800
According to question 100 K = 23800
⇒ K = 238
Q20: If the digits are not allowed to repeat in any number formed by using the digits 0, 2, 4, 6, 8, then the number of all numbers greater than 10,000 is equal to _____________.
Ans: 96
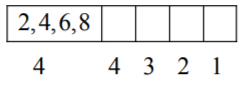
= 4 × 4 × 3 × 2 = 96
Q21: There are 15 players in a cricket team, out of which 6 are bowlers, 7 are batsman and 2 are wicketkeepers. The number of ways, a team of 11 players be selected from them so as to include at least 4 bowlers, 5 batsman and 1 wicketkeeper, is ______________.
Ans: 777
15 : Players
6 : Bowlers
7 : Batsman
2 : Wicket keepers
Total number of ways for :
at least 4 bowler, 5 batsman & 1 wicket keeper
= 6C4 (7C6 × 2C1 + 7C5 × 2C2) + 6C5 × 7C5 × 2C1
= 777
Q22: If  = α(11!), then the value of α is equal to ___________.
= α(11!), then the value of α is equal to ___________.
Ans: 160
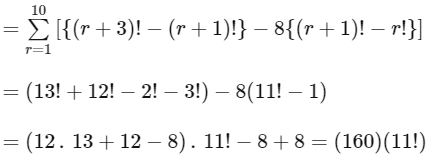
Therfore, α = 160
Q23: The number of times the digit 3 will be written when listing the integers from 1 to 1000 is :
Ans: 300
In single digit numbers = 1
In double digit numbers = 10 + 9 = 19
In triple digit numbers = 100 + 90 + 90 = 280
Total = 300 times
Q24: The missing value in the following figure is Ans: 4
Ans: 4
Inside number = (difference)difference(difference)!
=(Greater number - Smaller number)(Greater number - Smaller number)!
i.e. 1=(2−1)(2−1)!,
424 = (12−8)(12−8)!,
36 = (7 − 4)(7 − 4)!
∴ ? = (5 − 3)(5−3)!
∴ Required number = 22! = 22×1 = 4
Q25: The total number of numbers, lying between 100 and 1000 that can be formed with the digits 1, 2, 3, 4, 5, if the repetition of digits is not allowed and numbers are divisible by either 3 or 5, is _____________.
Ans: 32
The numbers are lying between 100 and 1000 then each number is of three digits.
The possible combination of 3 digits numbers are
1, 2, 3; 1, 2, 4; 1, 2, 5; 1, 3, 4; 1, 3, 5; 1, 4, 5; 2, 3, 4; 2, 3, 5; 2, 4, 5; and 3, 4, 5.
The possible combination of numbers which are divisible by 3 are 1, 2, 3; 3, 4, 5; 1, 3, 5 and 2, 3, 4.
(If sum of digits of a number is divisible by 3 then the number is divisible by 3)
∴ Total number of numbers = 4 × 3! = 24
The possible combination of numbers divisible by 5 are 1, 2, 5; 2, 3, 5; 3, 4, 5; 1, 3, 5; 1, 4, 5 and 2, 4, 5.
(If the last digit of a number is 0 or 5 then the number is divisible by 5)
∴ Total number of numbers = 6 × 2! = 12
The possible combination of number divisible by both 3 and 5 are 1, 3, 5 and 3, 4, 5.
∴ Total number of numbers = 2 × 2! = 4
∴ Total required number = 24 + 12 - 4 = 32
Q26: The students S1, S2, ....., S10 are to be divided into 3 groups A, B and C such that each group has at least one student and the group C has at most 3 students. Then the total number of possibilities of forming such groups is ___________.
Ans: 31650
If group C has one student then number of groups
= 10C1 [29 – 2] = 5100
If group C has two students then number of groups
= 10C2 [28 – 2] = 11430
If group C has three students then number of groups
= 10C3 × [27 – 2] = 15120
So total groups = 31650
|
446 docs|930 tests
|
FAQs on JEE Main Previous Year Questions (2025): Permutations and Combinations - Chapter-wise Tests for JEE Main & Advanced
| 1. What is the difference between permutations and combinations? |  |
| 2. How do you calculate the number of permutations of a set of objects? |  |
| 3. How do you calculate the number of combinations of a set of objects? |  |
| 4. What is the concept of repetition in permutations and combinations? |  |
| 5. Can you provide an example of a real-life application of permutations and combinations? |  |

























