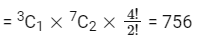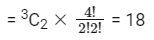[JEE Mains MCQs]
Q1: Two families with three members each and one family with four members are to be seated in a row. In how many ways can they be seated so that the same family members are not separated?
(a) 2! 3! 4!
(b) (3!)3.(4!)
(c) 3! (4!)3
(d) (3!)2.(4!)
Ans: (b)
F1 → 3 members
F2 → 3 members
F3 → 4 members
Total arrangements of three families = 3!
Arrangement between members of F1 family = 3!
Arrangement between members of F2 family = 3!
Arrangement between members of F3 family = 4!
∴ Total numbers of ways can they be seated so that the same family members are not separated = 3! × 3! × 3! × 4!
= (3!)3.(4!)
Q2: There are 3 sections in a question paper and each section contains 5 questions. A candidate has to answer a total of 5 questions, choosing at least one question from each section. Then the number of ways, in which the candidate can choose the questions, is :
(a) 2250
(b) 2255
(c) 3000
(d) 1500
Ans: (a)
 ∴ Total number of selection of 5 questions
∴ Total number of selection of 5 questions
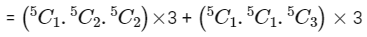
= 5 × 10 × 10 × 3 + 5 × 5 × 10 × 3
= 2250
Q3: The value of (2.1P0 – 3.2P1 + 4.3P2 .... up to 51th term)+ (1! – 2! + 3! – ..... up to 51th term) is equal to:
(a) 1
(b) 1 + (51)!
(c) 1 – 51(51)!
(d) 1 + (52)!
Ans: (d)
(2.1P0 – 3.2P1 + 4.3P2 .... up to 51th term)+ (1! – 2! + 3! – ..... up to 51th term)
= ( 2.1! - 3.2! + 4.3! - ....+ 52.51!)+ ( 1! – 2! + 3! – ..... + (51)! )
= (2! - 3! + 4! .....+ 52! )+ ( 1! - 2! + 3! - 4! + .....+ 51! )
= 1 + (52)!
Q4: Let n > 2 be an integer. Suppose that there are n Metro stations in a city located along a circular path. Each pair of stations is connected by a straight track only. Further, each pair of nearest stations is connected by blue line, whereas all remaining pairs of stations are connected by red line. If the number of red lines is 99 times the number of blue lines, then the value of n is:
(a) 201
(b) 199
(c) 101
(d) 200
Ans: (a)
 Number of blue lines = Number of sides = n
Number of blue lines = Number of sides = n
Number of red lines = number of diagonals = nC2 – n
According to question,
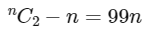
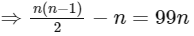
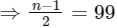
⇒ n = 201
Q5: If the number of five digit numbers with distinct digits and 2 at the 10th place is 336 k, then k is equal to:
(a) 6
(b) 8
(c) 4
(d) 7
Ans: (b)
 Except 1 and 2 there are eight options on first place and only one option at fourth place possible which is digit '2'.
Except 1 and 2 there are eight options on first place and only one option at fourth place possible which is digit '2'.
Remaining three places can be filled by any three digits out of 1, 3, 4, 5, 6, 7, 8 and 9.
∴ No. of five digits numbers = 8 × 8 × 7 × 1 × 6 = 336 × 8
Also 336k = 336 × 8
⇒ k = 8
Q6: If a, b and c are the greatest value of 19Cp, 20Cq and 21Cr respectively, then:
(a) a/11 = b/22 = c/21
(b) a/10 = b/11 = c/42
(c) a/10 = b/11 = c/42
(d) a/11 = b/22 = c/42
Ans: (d)
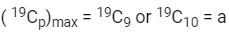

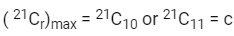
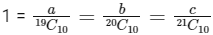

Q7: The number of ordered pairs (r, k) for which 6.35Cr = (k2 - 3). 36Cr+1, where k is an integer, is:
(a) 6
(b) 3
(c) 2
(d) 4
Ans: (d)
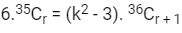
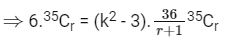
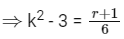
Possible values of r for integral values of k, are
r = 5, 35
number of ordered pairs are 4
(5, 2), (5, –2), (35, 3), (35, 3)
Q8: Total number of 6-digit numbers in which only and all the five digits 1, 3, 5, 7 and 9 appear, is :
(a) 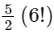
(b) 6!
(c) 56
(d) 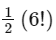
Ans: (a)
Here none number repeats more than once.
We can choose the number which repeats more than once among 1, 3, 5, 7, 9 in 5C1 ways.
Let number 3 repeats more than once. So six digits are 1, 3, 3, 5, 7, 9.
We can arrange those six digits in 6!/2! ways.
∴ Total six digit numbers 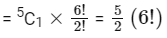
[JEE Mains Numericals]
Q9: The number of words (with or without meaning) that can be formed from all the letters of the word “LETTER” in which vowels never come together is ________.
Ans: 120
Consonants → LTTR
Vowels → EE
Total No of words = 6!/2!2! = 180
Total no of words if vowels are together
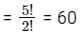
∴ Total no of words where
vowels never come together = 180 – 60 = 120.
Q10: Four fair dice are thrown independently 27 times. Then the expected number of times, at least two dice show up a three or a five, is _________.
Ans: 11
4 dice are independently thrown. Each die has probability to show 3 or 5 is
P = 2/6 = 1/3
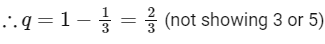
Experiment is performed with 4 dices independently
∴ Their binomial distribution is

∴ In one throw of each dice probability of showing 3 or 5 at least twice is
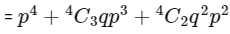
= 33/81
Given such experiment performed 27 times
∴ So expected outcomes = np
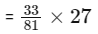
= 11
Q11: The number of words, with or without meaning, that can be formed by taking 4 letters at a time from the letters of the word ’SYLLABUS’ such that two letters are distinct and two letters are alike, is:
Ans: 240
In 'SYLLABUS' word
1. Two S letters
2. Two L letters
3. One Y letter
4. One A letter
5. One B letter
6. One U letter
Number of ways we can select two alike letters = 2C1
Then number of ways we can select two distinct letters = 5C2
Then total arrangement of selected letters = 4!/2!
So total number of words, with or without meaning, that can be formed
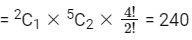
Q12: A test consists of 6 multiple choice questions, each having 4 alternative answers of which only one is correct. The number of ways, in which a candidate answers all six questions such that exactly four of the answers are correct, is __________.
Ans: 135
Select any 4 questions in 6C4 ways which are correct.
Answering right option for each question is possible in 1 way.
So ways of choosing right option for 4 questions = 1.1.1.1 = (1)4
Number of ways of choosing wrong option for each question = 3
So ways of choosing wrong option for 2 questions = (3)2
∴ Required number of ways = 6C4.(1)4.(3)2 = 135
Q13: The total number of 3-digit numbers, whose sum of digits is 10, is __________.
Ans: 54
Let xyz is 3 digits number.
Given that sum of digits = 10
∴ x + y + z = 10 ......(1)
Also x can't be 0 as if x = 0 then it will become 2 digits number.
So, x ≥ 1, y ≥ 0, z ≥ 0
As x ≥ 1
⇒ x − 1 ≥ 0
Let x − 1 = t
∴ t ≥ 0
From equation (1)
(x − 1) + y + z = 9
⇒ t + y + z = 9
Now this problem becomes, distributing 9 things among 3 people t, y, z.
Number of ways we can do that
= 9+3−1C3−1=11C2 = 55
Now when 3 digit number is 900 then t = 9, y = 0, z = 0.
And when t = 9, then
x − 1 = 9
⇒ x = 10
But we can't take x = 10 in a 3 digits number. So, we have to remove this case.
∴ Total number of 3 digit numbers = 55 − 1 = 54.
Q14: If the letters of the word 'MOTHER' be permuted and all the words so formed (with or without meaning) be listed as in a dictionary, then the position of the word 'MOTHER' is ______.
Ans: 309
Step 1: Write all the alphabets in alphabetical order.
 Step 2: Give a number to each alphabet starting from 0 in alphabetical order.
Step 2: Give a number to each alphabet starting from 0 in alphabetical order.
 Step 3 : In Word "MOTHER" first alphabet is 'M' which is present in the 2nd position in the Alphabet Box. And after 'M', in the word "MOTHER" there are 5 alphabets "OTHER" which we can arrange in 5! Ways.
Step 3 : In Word "MOTHER" first alphabet is 'M' which is present in the 2nd position in the Alphabet Box. And after 'M', in the word "MOTHER" there are 5 alphabets "OTHER" which we can arrange in 5! Ways.
So for Alphabet 'M' we write 2x5!
As in word "MOTHER" we calculated 'M', so delete 'M'
Step 4: From Alphabet box and check remaining alphabets got right numbers or not in Alphabet box. As you can see after deleting 'M' 2nd position in the Alphabet box is missing so we have to create a new alphabet table.
 Step 5: Now next alphabet after 'M' in word "MOTHER" is 'O' which is present in the 2nd position in the New Alphabet Box. And after 'O'in the word "MOTHER" there are 4 alphabets "THER" which we can arrange in 4! Ways.
Step 5: Now next alphabet after 'M' in word "MOTHER" is 'O' which is present in the 2nd position in the New Alphabet Box. And after 'O'in the word "MOTHER" there are 4 alphabets "THER" which we can arrange in 4! Ways.
So for Alphabet 'O' we write 2 x4!
Step 6: Now as in word "MOTHER" we calculated 'O', so delete 'O' from Alphabet box and check remaining alphabets got right numbers or not in Alphabet box. As you can see after deleting 'O' 2nd position in the Alphabet box is missing so we have to create a new alphabet table.
 Step 7: Now next alphabet after 'O' in word "MOTHER" is T which is present in the 3rd position in the New Alphabet Box. And after T in the word "MOTHER" there are 3 alphabets "HER" which we can arrange in 3! Ways.
Step 7: Now next alphabet after 'O' in word "MOTHER" is T which is present in the 3rd position in the New Alphabet Box. And after T in the word "MOTHER" there are 3 alphabets "HER" which we can arrange in 3! Ways.
So for Alphabet T we write 3x3!
Step 8: Now as in word "MOTHER" we calculated T , so delete T from Alphabet box and check remaining alphabets got right numbers or not in Alphabet box. As you can see after deleting T all other alphabets remains in correct position so new alphabet box will be same.
 Step 9: Now next alphabet after T in word "MOTHER" is 'H' which is present at the 1st position in the New Alphabet Box. And after 'H' in the word "MOTHER" there are 2 alphabets "ER" which we can arrange in 2! Ways.
Step 9: Now next alphabet after T in word "MOTHER" is 'H' which is present at the 1st position in the New Alphabet Box. And after 'H' in the word "MOTHER" there are 2 alphabets "ER" which we can arrange in 2! Ways.
So for Alphabet 'H' we write 1 x 2!
Step 10: Now as in word "MOTHER" we calculated 'H', so delete 'H' from Alphabet box and check remaining alphabets got right numbers or not in Alphabet box. As you can see after deleting 'H' 1st position in the Alphabet box is missing so we have to create a new alphabet table.
 Step 11: Now next alphabet after 'H' in word "MOTHER" is 'E' which is present in the 0tn position in the New Alphabet Box. And after 'E' in the word "MOTHER" there are 1 alphabet "R" which we can arrange in 1! Ways.
Step 11: Now next alphabet after 'H' in word "MOTHER" is 'E' which is present in the 0tn position in the New Alphabet Box. And after 'E' in the word "MOTHER" there are 1 alphabet "R" which we can arrange in 1! Ways.
So for Alphabet 'E' we write 0 x 1!
Step 12: Now as in word "MOTHER" we calculated 'E', so delete 'E' from Alphabet box and check remaining alphabets got right numbers or not in Alphabet box. As you can see after deleting 'E' 0th position in the Alphabet box is missing so we have to create a new alphabet Box.
 Step 13: Now next alphabet after 'E' in word "MOTHER" is 'R' which is present in the 0,h position in the New Alphabet Box. And after 'R' in the word "MOTHER" there are no alphabet so it is the last alphabet.
Step 13: Now next alphabet after 'E' in word "MOTHER" is 'R' which is present in the 0,h position in the New Alphabet Box. And after 'R' in the word "MOTHER" there are no alphabet so it is the last alphabet.
So for last Alphabet 'R' we always write 0!
Position of the word 'MOTHER' in the dictionary
= 2 x51 + 2 x 4 ! + 3 x 3! + 1 x 2! + 0 x 1! + 0!
= 240 + 48 + 18 + 2 + 1
= 309
Q15: The number of 4 letter words (with or without meaning) that can be formed from the eleven letters of the word 'EXAMINATION' is _______.
Ans: 2454
2A, 2I, 2N, E, X, M, T, O
To form four letter words
Case 1 : All same ( not possible)
Case 2 : 1 different, 3 same (not possible)
Case 3 : 2 different, 2 same
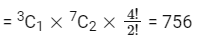
Case 4 : 2 same of one kind, 2 same same of other kind
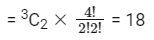
Case 5 : All letters are different
= 8C4 × 4! = 1680
∴ Total ways = 1680 + 756 + 18 = 2454
Q16: An urn contains 5 red marbles, 4 black marbles and 3 white marbles. Then the number of ways in which 4 marbles can be drawn so that at the most three of them are red is ___________.
Ans: 490
Here 5 red marbels and 7 non red marbels presents.
No of ways 4 marbels can be chosen where atmost 3 red marbels can be present.
Case 1: When 3 red marbels present
No of ways = 5C3 × 7C1
Case 2: When 2 red marbels present
No of ways = 5C2 × 7C2
Case 3: When 1 red marbels present
No of ways = 5C1 × 7C3
Case 4: When 0 red marbels present
No of ways = 5C0 × 7C4
∴ Total number of ways
= 5C3 × 7C1 + 5C2 × 7C2 + 5C1 × 7C3 + 5C0 × 7C4
= 70 + 210 + 175 + 35
= 490
 ∴ Total number of selection of 5 questions
∴ Total number of selection of 5 questions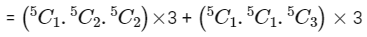
 Number of blue lines = Number of sides = n
Number of blue lines = Number of sides = n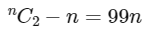
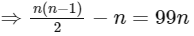
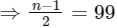
 Except 1 and 2 there are eight options on first place and only one option at fourth place possible which is digit '2'.
Except 1 and 2 there are eight options on first place and only one option at fourth place possible which is digit '2'.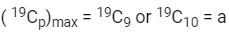

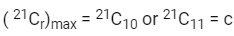
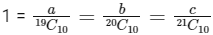

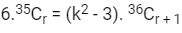
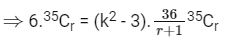
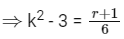
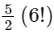
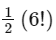
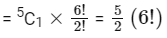
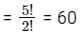
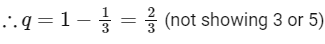

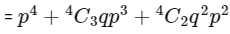
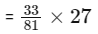
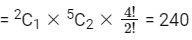
 Step 2: Give a number to each alphabet starting from 0 in alphabetical order.
Step 2: Give a number to each alphabet starting from 0 in alphabetical order. Step 3 : In Word "MOTHER" first alphabet is 'M' which is present in the 2nd position in the Alphabet Box. And after 'M', in the word "MOTHER" there are 5 alphabets "OTHER" which we can arrange in 5! Ways.
Step 3 : In Word "MOTHER" first alphabet is 'M' which is present in the 2nd position in the Alphabet Box. And after 'M', in the word "MOTHER" there are 5 alphabets "OTHER" which we can arrange in 5! Ways. Step 5: Now next alphabet after 'M' in word "MOTHER" is 'O' which is present in the 2nd position in the New Alphabet Box. And after 'O'in the word "MOTHER" there are 4 alphabets "THER" which we can arrange in 4! Ways.
Step 5: Now next alphabet after 'M' in word "MOTHER" is 'O' which is present in the 2nd position in the New Alphabet Box. And after 'O'in the word "MOTHER" there are 4 alphabets "THER" which we can arrange in 4! Ways. Step 7: Now next alphabet after 'O' in word "MOTHER" is T which is present in the 3rd position in the New Alphabet Box. And after T in the word "MOTHER" there are 3 alphabets "HER" which we can arrange in 3! Ways.
Step 7: Now next alphabet after 'O' in word "MOTHER" is T which is present in the 3rd position in the New Alphabet Box. And after T in the word "MOTHER" there are 3 alphabets "HER" which we can arrange in 3! Ways. Step 9: Now next alphabet after T in word "MOTHER" is 'H' which is present at the 1st position in the New Alphabet Box. And after 'H' in the word "MOTHER" there are 2 alphabets "ER" which we can arrange in 2! Ways.
Step 9: Now next alphabet after T in word "MOTHER" is 'H' which is present at the 1st position in the New Alphabet Box. And after 'H' in the word "MOTHER" there are 2 alphabets "ER" which we can arrange in 2! Ways. Step 11: Now next alphabet after 'H' in word "MOTHER" is 'E' which is present in the 0tn position in the New Alphabet Box. And after 'E' in the word "MOTHER" there are 1 alphabet "R" which we can arrange in 1! Ways.
Step 11: Now next alphabet after 'H' in word "MOTHER" is 'E' which is present in the 0tn position in the New Alphabet Box. And after 'E' in the word "MOTHER" there are 1 alphabet "R" which we can arrange in 1! Ways. Step 13: Now next alphabet after 'E' in word "MOTHER" is 'R' which is present in the 0,h position in the New Alphabet Box. And after 'R' in the word "MOTHER" there are no alphabet so it is the last alphabet.
Step 13: Now next alphabet after 'E' in word "MOTHER" is 'R' which is present in the 0,h position in the New Alphabet Box. And after 'R' in the word "MOTHER" there are no alphabet so it is the last alphabet.