Chemical Kinetics: Reaction Rate, Order & Molecularity | Chemistry for JEE Main & Advanced PDF Download
What is Chemical Kinetics?
Chemistry is all about things changing. When certain substances mix, they transform into something new. Chemists study these changes and want to know:
- If a change can happen, predicted by thermodynamics (where a change is possible if things go from disorder to order).
- The extent to which a reaction will proceed.
- How fast does a change happen, and what time does it take to finish?
Understanding how fast things change is as important as knowing if and how much they change. Chemical kinetics is the part of chemistry that looks at how fast changes happen and why.
It answers questions like:
- Why does food go bad quickly?
- How do we make materials for fixing teeth that harden fast?
- Why does fuel burn quickly in a car?
 Some Chemical Reactions in Daily Life
Some Chemical Reactions in Daily Life
- 'Kinetics,' means movement, it helps us understand the speed of changes. Unlike thermodynamics, which says if a change is possible, chemical kinetics tells us how quickly it will happen. For example, even though it's predicted that a diamond can turn into graphite, it happens so slowly that we think "diamonds are forever."
- Studying kinetics not only tells us how fast a change happens but also what makes it speed up or slow down. Things like how much stuff is there, the temperature and special helpers called catalysts can make changes go faster or slower. We look at both big amounts and tiny details like how molecules bump into each other to understand these changes.
- In this document, we'll learn about how fast changes happen and what factors affect them. We'll also talk a bit about the collision theory of reaction rates. To start, let's dig into the details of how fast changes happen.
Understanding Reaction Rate
Some reactions happen really fast, like when silver chloride forms instantly by mixing silver nitrate and sodium chloride solutions. On the flip side, some reactions are super slow, like iron rusting when exposed to air and moisture. There are also reactions, like sugar inversion and starch hydrolysis, that go at a medium speed. Can you think of more examples for each type?
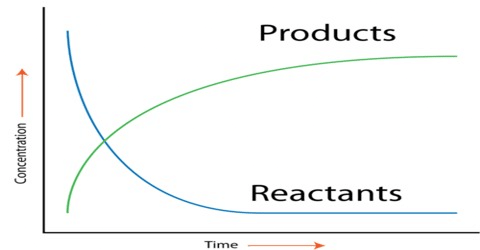 Change in Concentrations
Change in Concentrations
Just like we measure the speed of a car by how much distance it covers in a certain time, we can measure the speed of a reaction by how the concentration of a substance changes over time. Specifically, we can express it as:
- The rate of decrease in the concentration of a reactant, or
- The rate of increase in the concentration of a product.
Let's take an example: if one thing (let's call it R) turns into another thing (let's call it P), and we measure their concentrations at different times, we can calculate the average rate of the reaction over that period.
For instance, if the concentration of R at time t1 is [R]1 and at time t2 is [R]2, and the same for product P, then:
- Change in concentration of R, Δ[R] = [R]2 – [R]1,
- Change in concentration of P, Δ[P] = [P]2 – [P]1.
The square brackets in the above expressions are used to express molar concentration.
- Rate of disappearance of R= Decrease in the concentration of R/Time taken = -Δ[R]/ Δt,
- Rate of appearance of P= Increase in the concentration of P/ Time taken = Δ[P]/ Δt
Since the concentration of reactants decreases, we make the rate a positive number by multiplying Δ[R] by -1. These equations give us the average rate of the reaction, which depends on how much the concentrations change and the time it takes for that change.
The formulas mentioned above show the average rate of a reaction, called "rav" This average rate relies on how much the concentration of substances like reactants or products changes and the time it takes for that change to happen.
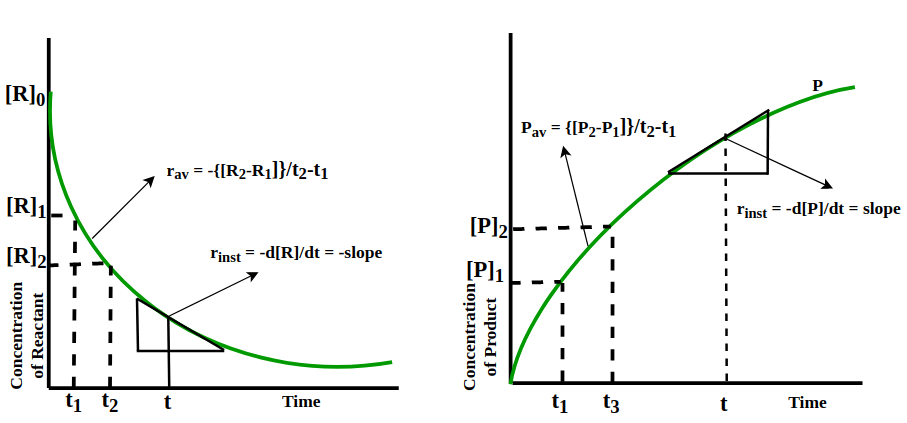 Instantaneous and Average Rate of Reaction
Instantaneous and Average Rate of Reaction
Example 1: Suppose the concentration of a reactant A changes from 0.4 M to 0.1 M in a time interval of 20 seconds. Calculate the rate of the reaction.
Answer: The rate of the reaction (r) can be calculated using formula:
r= Δ[A]/Δt
r = (0.1M−0.4M)/20s
r= −0.3M/20s
r=−0.015M/s
Note: The negative sign indicates a decrease in the concentration of the reactant, which is typical for reactants in a chemical reaction.So, in this example, the rate of the reaction is −0.015M/s
Units of the Rate of a Reaction
The equations above show us that the units of reaction rate are concentration per unit time. For instance, if the concentration is in mol/L and time is in seconds, then the units will be mol/L·s. However, in gas reactions, if we express concentrations in terms of partial pressures, then the units of the rate equation will be atm/s.
- While the average rate is helpful, it can't predict the speed of a reaction at a specific moment because it stays constant for the time it's calculated. So, to know the rate at a particular instant, we find the instantaneous rate.
- It's calculated when we consider the average rate at the smallest time interval, say dt (when Δt approaches zero). Mathematically, for an incredibly small dt, the instantaneous rate is given by:
As Δt → 0 or rinst = -d[R]/dt = d[P]/dt
- In a reaction where stoichiometric coefficients are the same, like Hg + Cl2 → HgCl2, the rate is given by the disappearance of reactants being the same as the appearance of products.
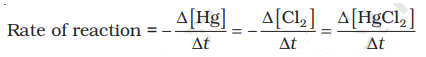
- However, in a reaction like 2HI(g) → H2(g) + I2(g), where stoichiometric coefficients aren't equal, the rate is given by dividing the change in concentration of HI by 2 to balance the equation.

- Similarly, for the reaction 5 Br- (aq) + BrO3– (aq) + 6 H+ (aq) → 3 Br2 (aq) + 3 H2O (l), the rate is expressed as:
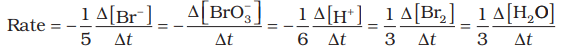
- In gaseous reactions at a constant temperature, concentration is proportional to partial pressure, so the rate can also be expressed as the rate of change in partial pressure of the reactant or the product.
Example 2: In a chemical reaction, N2 + 3H2 → 2 NH3 the rate of (d[NH3]/dt) = 2 × 10−4. How to calculate the value of (−d[H2]/dt) by kinetics equation?
Answer: From the rate equation for the formation of ammonia from nitrogen and hydrogen,
d[H2]/dt = (3/2) × 2 × 10−4 mol lit−1 sec−1
= 3 × 10−4 mol lit−1 sec−1
Example 3: The rate of formation of NO(g) in the reaction NOBr(g)→ NO(g) Br2(g) is found to be 1.6 × 10-4 M/s. Find the rate of overall reaction rate and rate of consumption of NOBr.
Answer: We have :
1.6 × 10-4 M/s.
First write a balanced chemical equation. 2NOBr(g) → 2NO(g) Br2(g)
Now, Rate of overall reaction =
=
=
= 0.8 × 10-4 M/s
Rate of consumption of NOBr = -
= 1.6 × 10-4 M/s
Rate Law and Rate Constant
- As time passes, the rate of a reaction tends to decrease because the concentration of reactants goes down. On the flip side, rates usually go up when the concentrations of reactants increase. Therefore, the rate of a reaction is influenced by the concentration of reactants.
- Imagine a general reaction like aA + bB → cC + dD where a, b, c, and d are numbers telling us how much of each thing is involved. The rate expression for this reaction is:
- Rate ∝ [A]x [B]y where exponents x and y might be the same or different from the numbers (a and b) in the reaction.
This expression can also be written as:
Rate = k [A]x [B]y where k is a constant called the rate constant.
Another way to express it is:
Rate = k d([A]x [B]y) / dt
This is known as the differential rate equation, where k is the rate constant.
- The equation which relates the rate of a reaction to the concentration of reactants is called the rate law or rate expression. The rate law shows the reaction rate in terms of the amount of reactants with each term raised to some power. This power might be the same as or different from the numbers in the balanced chemical equation.
- For example, in the reaction 2NO(g) + O2(g) → 2NO2(g), we can measure the rate by keeping the concentration of one reactant constant and changing the other, or by changing both concentrations.
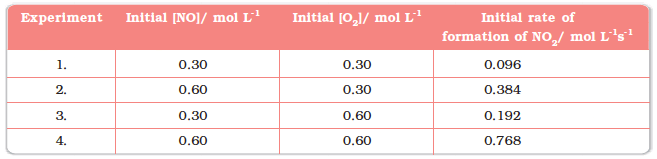 Initial Rate of Formation of NO2
Initial Rate of Formation of NO2
- It's clear from the results that when we double the concentration of NO and keep O2 constant, the initial rate increases four times from 0.096 to 0.384 mol/L·s. This shows that the rate depends on the square of the concentration of NO. Similarly, when we keep the concentration of NO constant and double the concentration of O2, the rate doubles, indicating that the rate depends on the concentration of O2 to the first power. So, the rate equation for this reaction is:
Rate = k [NO]2 [O2]
The differential form of this rate expression is given as:
d[R] / dt = k [NO]2 [O2]
- Now, we see that for this reaction, the exponents in the rate equation derived from experimental data match the stoichiometric coefficients in the balanced chemical equation.
Here are some other examples:
- Reaction: CHCl3 + Cl2 → CCl4 + HCl
Experimental rate expression: Rate = k [CHCl3]1 [Cl2]1/2 - Reaction: CH3COOC2H5 + H2O → CH3COOH + C2H5OH
Experimental rate expression: Rate = k [CH3COOC2H5]1 [H2O]0
In these reactions, the exponents in the rate expressions don't match the stoichiometric coefficients. Therefore, we can conclude that the rate law for any reaction cannot be predicted just by looking at the balanced chemical equation; it must be determined experimentally.
Order of a Reaction
The order of a reaction refers to the power to which the concentration of a reactant is raised in the rate equation (rate law) for that particular reaction.
By performing a reaction in actual in laboratory and carefully examining it, it is possible to express the rate law as the product of concentrations of reactants each raised to some power.
For example consider the reaction : aA+ bB → cC +dD. The differential rate law is written as :
Rate = =
=
=
= kr[A]m[B]n
where kr is called as rate constant of the reaction or velocity constant or specific Reaction rate.
k is a characteristic of a reaction at a given temperature. It changing only when the temperature changes.
The powers m and n are integers or fractions. m is called as order of reaction with respect to A and n is called as order of reaction with respect to B.The overall order of reaction = m n
Hence, the sum of powers of the concentration of the reactants in the rate law expression is called the order of that chemical reaction.
- The values of m and n are calculated from the experimental data obtained for a reaction and the powers m and n are not related to the stoichiometric coefficients of the reactants
- Order can be fractional, zero or negative.
For example consider the following reaction :
(i) H2(g) Br2(g) → 2 HBr (g) rate = k[H2] [Br2]1/2 (by experiment), order of reaction = 1 1/2 = 3/2
(ii) CH3CHO(g) → CH4(g) CO(g), rate = k[CH3CHO]3/2 , order of reaction = 3/2
Units of k:
In general, the rate law for a nth order reaction can be taken as :
where k : rate constant; c : concentration and n : order of reaction
⇒ ⇒ Units of k º (mol/L)1-n (time)-1
For a 'zero' order reaction (n = 0) : Units of k = (mol/L)1 (time)-1 or mol/L/sec
For a first order reaction (n = 1) : Units of k º (time)-1 e.g. sec-1, min-1, hrs-1 etc.
For a second order reaction (n = 2) : Units of k º (mol/L)-1 (time)-1 or L/mol/sec.
For a general reaction:
aA + bB → cC + dD
Rate = k [A]x [B]y
Where x + y = n (the order of the reaction) and
k = x (Rate / [A]x [B]y)

The units of k for different reaction orders are listed in the table below.
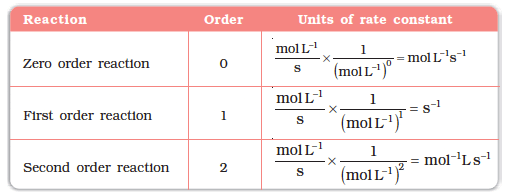 Units of Rate Constant
Units of Rate Constant
Example 4: The rate constant of a reaction is k=3.28×10-4 s-1. Find the order of the reaction.
a) Zero order
b) First order
c) Second order
d) Third order
Answer: b) First order
Explanation: Given, k= 3.28×10-4 s-1
The standard formula for calculating rate constant units is k=(mol L-1)1-ns-1, where ‘n’ is the reaction order. The value of ‘n’ must be 1 for (mol L-1)1-ns-1 to be s-1. As a result, k=3.28×10-4s-1 denotes a first-order reaction.
Example 5: From the rate laws for the reactions given below, determine the order with respect to each species and the overall order.
(i) 2HCrO4- + 6I- + 14H → 2Cr3+ + 3I2+8H2O, Rate = k[HCrO4-] [I-]2 [H ]2
(ii) H2O2 +2I- +2H → I2 +2H2O, Rate = k[H2O2] [I-]
Sol.
(i) The order of the reaction with respect to [HCrO4-] is 1; with respect to [I-] is 2 and with respect to [H ] is 2. The overall order of the reaction is 1 +2 +2 = 5(ii) The order of the reaction with respect to [H2O2] is 1 and with respect to [I-] is 1. The overall order of the reaction is 1 +1= 2.
Note:
- In (i) stoichiometric coefficient of I- is 6 whereas the power coefficient (n) in the rate law is 2.
- Reaction (i) may not take place in a single step. It may not be possible for all the 22 molecules to be in a state to collide with each other simultaneously. Such a reaction is called a complex reaction.
- A complex reaction takes place in a series of a number of elementary reactions.
Molecularity of a Reaction
Another characteristic of a reaction, called molecularity, helps us understand how a reaction happens. Molecularity is the number of reacting species (like atoms, ions, or molecules) that must collide simultaneously to bring about a chemical reaction in an elementary reaction.
The number of reacting species (atoms, ions or molecules) taking part in an elementary reaction, which must collide simultaneously in order to bring about a chemical reaction is called molecularity of a reaction.
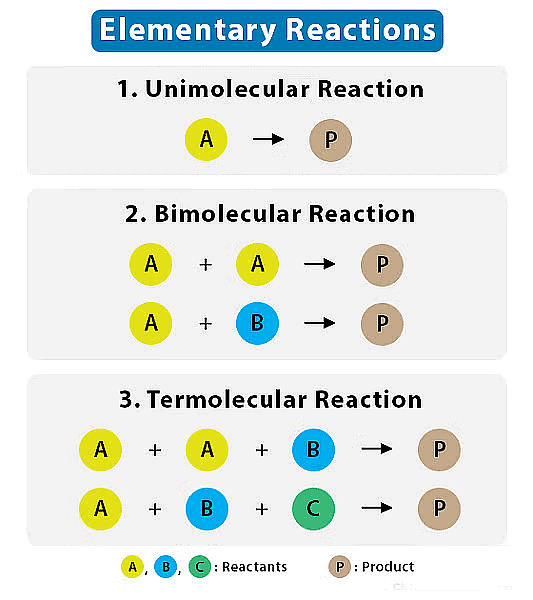
- Elementary reaction is a simple, single-step chemical reaction that involves a small number of reactant species and leads directly to the formation of products.
- Molecularity is a concept used specifically for elementary reactions, and it is not applicable to overall or complex reactions.
The molecularity of a reaction is often classified into three categories:
1. Unimolecular (Molecularity = 1)
- In a unimolecular reaction, a single molecule is involved in the elementary reaction. The rate equation for a unimolecular reaction is often expressed as: Rate=k[A]
- An example of a unimolecular reaction is a first-order reaction, where a single molecule undergoes a reaction, and the rate is directly proportional to its concentration.
- Cyclopropane → propene
- O3(g) → O2(g) + O(g)
- N2O5(g) → N2O4(g) +1/2O2(g)
2. Bimolecular (Molecularity = 2)
- In a bimolecular reaction, two molecules come together to react in a single step. The rate equation for a bimolecular reaction is often expressed as:
Rate=k[A][B]
- An example of a bimolecular reaction is a second-order reaction, where the rate is proportional to the product of the concentrations of two reactants.
1. NO(g) + O3 (g) → NO2(g)+ O2(g)
2. 2HI(g) → H2(g) I2(g)
3. Termolecular (Molecularity = 3)
- In a termolecular reaction, three molecules collide and react simultaneously in a single step. Termolecular reactions are relatively rare because they require the simultaneous collision of three reactant molecules, which is less likely to occur. They are more common in gas-phase reactions.
- Termolecular reactions are not as frequently encountered as unimolecular or bimolecular reactions.
It's important to note that molecularity is a theoretical concept used to describe elementary reactions. In more complex reactions, which involve multiple elementary steps, the reaction order and molecularity may not be the same. Overall reaction orders are determined experimentally, while molecularity is a concept used to describe the individual elementary steps of a reaction mechanism.
 Some More Examples of The Molecularity of a Reaction
Some More Examples of The Molecularity of a Reaction
Difference Between Order and Molecularity of a Reaction

Complex reactions involving more than three molecules in the stoichiometric equation must take place in more than one step. For example, the reaction:
KClO3 + 6FeSO4 + 3H2SO4 → KCl + 3Fe2(SO4)3 + 3H2O
- Although this reaction seems to be a tenth-order one, it's actually a second-order reaction occurring in multiple steps. This tells us that the reaction happens in several stages. Now, the question arises: which step determines how fast the entire reaction occurs? The answer becomes clear when we look at the mechanism of the reaction.
- Think of it like a relay race competition. The chances of winning the competition for a team depend on the slowest person in the team. Similarly, the overall speed of the reaction is controlled by the slowest step in a reaction, and this step is called the rate-determining step.
Consider the decomposition of hydrogen peroxide catalyzed by iodide ion in an alkaline medium:
2H2O2 + I– (Alkaline medium) → 2H2O + O2
The equation describing the rate of this reaction is:
-d[H2O2] / dt = k [H2O2][I–]
This means the reaction is first order with respect to both H2O2 and I–. This reaction takes place in two steps:
1. H2O2 + I– → H2O + IO–
2. H2O2 + IO– → H2O + I– + O2
In both steps, we have bimolecular elementary reactions. A species called IO– is formed as an intermediate during the reaction, but it doesn't appear in the overall balanced equation. The first step, which is slow, is known as the rate-determining step. So, the speed at which the intermediate is formed will dictate the overall rate of this reaction.
So we can conclude that:
- The order of a reaction is an experimental quantity, which can be zero or a fraction, but molecularity cannot be zero or a non-integer.
- Order applies to both elementary and complex reactions, while molecularity is only applicable to elementary reactions.
- For a complex reaction, the order is determined by the slowest step, and the molecularity of the slowest step is the same as the order of the overall reaction.
Example 6: The rate of formation of NO(g) in the reaction NOBr(g)→ NO(g) Br2(g) is found to be 1.6 × 10-4 M/s. Find the rate of overall reaction rate and rate of consumption of NOBr.
Solution: We have :
1.6 × 10-4 M/s.
First write a balanced chemical equation. 2NOBr(g) → 2NO(g) Br2(g)
Now, Rate of overall reaction =
=
=
= 0.8 × 10-4 M/s
Rate of consumption of NOBr = -
= 1.6 × 10-4 M/s
Example 7: The rate constant for a given reaction is k = 3 × 10-5 s-1 atm-1. Express it in units of L mol-1 sec-1.
Solution: PV = nRT ⇒ P = cRT (c : concentration in mol/L)
Substitute R = 0.0821 L-atm/mol/K ; T = 273 K ; P = 1 atm ⇒ c = 0.04462 mol/L
⇒
= 6.73 × 10-4 L/mol/s.
Example 8: From the rate laws for the reactions given below, determine the order with respect to each species and the overall order.
(i) 2HCrO4- + 6I- + 14H → 2Cr3 + 3I2+8H2O, Rate = k[HCrO4-] [I-]2 [H ]2
(ii) H2O2 +2I- +2H → I2 +2H2O, Rate = k[H2O2] [I-]
Solution: (i) The order of the reaction with respect to [HCrO4-] is 1; with respect to [I-] is 2 and with respect to [H ] is 2. The overall order of the reaction is 1 +2 +2 = 5
(ii) The order of the reaction with respect to [H2O2] is 1 and with respect to [I-] is 1. The overall order of the reaction is 1 +1= 2.
- In (i) stoichiometric coefficient of I- is 6 whereas the power coefficient (n) in the rate law is 2.
- Reaction (i) may not take place in a single step. It may not be possible for all the 22 molecules to be in a state to collide with each other simultaneously. Such a reaction is called a complex reaction.
- A complex reaction takes place in a series of a number of elementary reactions.
|
361 videos|822 docs|301 tests
|
FAQs on Chemical Kinetics: Reaction Rate, Order & Molecularity - Chemistry for JEE Main & Advanced
| 1. What is chemical kinetics? |  |
| 2. How is reaction rate defined in chemical kinetics? |  |
| 3. What is the rate law and rate constant in chemical kinetics? |  |
| 4. What is the order of a reaction in chemical kinetics? |  |
| 5. What is molecularity in chemical kinetics? |  |
















