Quadratic Equations | Physics for JEE Main & Advanced PDF Download

What is a Quadratic  Equation?

A quadratic equation in the variable x is an equation of the form ax² + bx + c = 0, where a, b, c are real numbers and a ≠ 0 is called the standard form of a quadratic equation.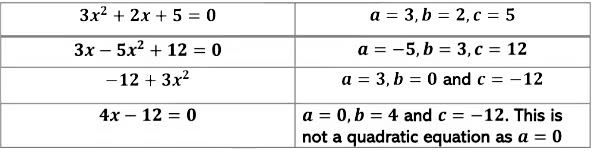

Example 1: Check whether the following are quadratic equations
(i) (x + 1)² = 2(x − 3)
⇒ (x + 1)² = x² + 2x + 1
∵ (a + b)² = a² + 2ab + b²
⇒ x² + 2x + 1 = 2(x − 3)
⇒ x² + 2x + 1 = 2x − 6
⇒ x² + 2x + 1 − 2x + 6 = 0
⇒ x² + 2x − 2x + 6 + 1 = 0
x² + 7 = 0
The above equation is a quadratic equation, where the coefficient of x is zero, i.e. b = 0

(ii) x(x + 1)(x + 8) = (x + 2)(x − 2)
LHS
⇒ x(x + 1)(x + 8)
⇒ x(x² + 8x + x + 8)
⇒ x(x² + 9x + 8)
⇒ x³ + 9x² + 8x
RHS
(x + 2)(x − 2)
⇒ x² − 4
∵ (a + b)(a − b) = a² − b²
Now, x³ + 9x² + 8x = x2 − 4
⇒ x³ + 9x² − x² + 8x + 4 = 0
x³ + 8x² + 8x + 4 = 0
It is not a quadratic equation as it is an equation of degree 3.

(iii) (x − 2)² + 1 = 2x − 3
LHS
(x − 2)² + 1 = x² − 2x + 4 + 1
∵ (a − b)² = a² − 2ab + b²
= x² − 2x + 5
RHS
2x − 3
⇒ x² − 2x + 5 = 2x − 3
⇒ x² − 2x − 2x + 5 + 3 = 0
⇒ x² − 4x + 8 = 0
The above equation is quadratic as it is of the form,
ax² + bx + c = 0

Example 2: The product of two consecutive positive integers is 420. Form the equation satisfying this scenario.
Let the two consecutive positive integers be x and x + 1 Product of the two consecutive integers= x(x + 1) = 420
⇒ x² + x = 420
⇒ x² + x − 420 = 0
x² + x − 420 = 0, is the required quadratic equation and the two integers satisfy this quadratic equation.

Clear all your JEE doubts with EduRev Join for Free

Join for Free

Solution of Quadratic Equation by Factorisation

A real number α is called a root of the quadratic equation x² +bx + c = 0 , a ≠ 0 if aα² + bα + c = 0
We say that x = α is a solution of the quadratic equation.
Example: x² − 2x − 3 = 0
If we put x = −1 in the LHS of the above equation we get,
(−1)² − 2(−1) − 3
1 + 2 − 3 = 0
Thus x = −1 is a solution of the equation x² − 2x − 3 = 0.
To find the roots of the quadratic equations we follow these steps.

Example 3: Find the roots of the equation x² − 3x − 10 = 0
The given equation is x² − 3x − 10 = 0.
Here a = 1, b = −3 and c = −10
(1) Find the product of a and c.
Here, the product of a and c= -10 → (ac) is negative

(2) Write the factors of this product (ac) such that the sum of the two factors is equal to b.
∴ ac = m × n and m + n = b
Factors of 10 = 2×5
Let m = −5 and n = 2 → (ac=-10)
We write the given equation as,
x² − 5x + 2x − 10 = 0
x(x − 5) + 2(x − 5) = 0
x − 5 x + 2 = 0
Equate each factor to zero to get the roots of the equation.
x − 5 = 0 and x + 2 = 0
x = 5, −2
Therefore, 5 and -2 are the roots of the equation x² − 3x − 10 = 0

Example 4: Solve the following quadratic equation by factorisation method.
i) 4√3x²  + 5x − 2√3  = 0
The given equation is 4√3x²  + 5x − 2√3  = 0
Here, a = 4√3 , b = 5 and c = −2√3
The product of a and c
= 4√3  × (−2√3 )
= −8 × 3
= −24
Factors of 24 = 3×8 and 8 + (−3) = 5
The factors of the equation are 8, − 3
So, the given equation can be written as,
4√3x²  + (8 − 3)x − 2√3  = 0
⇒ 4 √3x² + 8x − 3x − 2√3  = 0
⇒ 4x( √3x + 2) −√3 (√3 x + 2) = 0
⇒ (4x − √3 )(√3x + 2) = 0
Equating each factor to zero we get,
(4x −√3 )=0 and (√3x + 2) = 0

The roots of the equation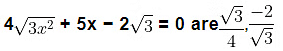


The given equation is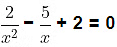
Multiplying the above equation by x² we get,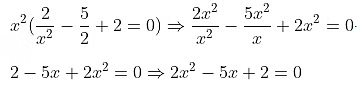

Here, a = 2, b = −5 and c = 2
The product of a and c = 2 × 2 = 4
The factors of 4 = 4 × 1 and 4 + 1 = 5
2x² − (4 + 1)x + 2 = 0
⇒ 2x² − 4x − 1x + 2 = 0
2x(x − 2) − (x − 2) = 0
(2x − 1)(x − 2) = 0
Equating each factor to zero we get,
(2x − 1) = 0 and (x − 2) = 0
x =  1/2 and x = 2
The roots of equation 2x² − 5x + 2 = 0 are  1/2  and 2

Example 5: The altitude of a right-angled triangle is 7 cm less than its base. If the hypotenuse is 13 cm long, then find the other two sides.
Let the length of the base be x cm, then altitude = x − 7 cm
Hypotenuse = 13 cm
We know, H² = P² + B²
132 = (x − 7)² + x² 
⇒ 169 = x² − 14x + 49 + x²
⇒ x² − 14x + 49 + x² = 169
⇒ 2x² − 14x + 49 − 169 = 0
⇒ 2x² − 14x − 120 = 0
Dividing the above equation by 2 we get,
x² − 7x − 60 = 0
Here, a = 1, b = −7 and c = −60
The product of a and c = 1 × (−60) = −60
The factors of 60 = 5 × 12 and −12 + 5 = 7
The given equation can be written as,
x² − 12x + 5x − 60 = 0
x(x − 12) + 5(x − 12) = 0
⇒ (x + 5)(x − 12) = 0
Equating each factor to zero we get,
(x + 5) = 0 and (x − 12) = 0
⇒ x = −5 and x = 12
The length of the base cannot be negative.
Therefore, Base = 12 cm
Altitude = x − 7 cm = 12 − 7 = 5 cm, Hypotenuse = 13 cm

Test: Maxima and Minima

Start Test

Start Test

Nature of Roots

The roots of the quadratic equation ax² + bx + c = 0 are given by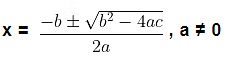

Where D = √b² − 4ac is called the discriminant.
This formula is known as the Quadratic Formula.
The nature of the roots depends upon the value of Discriminant, D.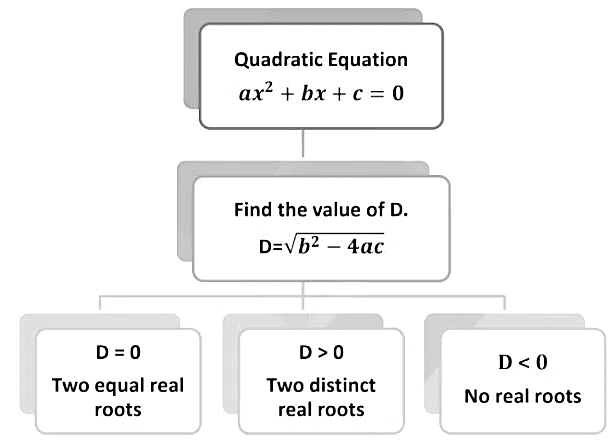

Example 6: Find the roots of the equation,

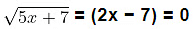
The given equation is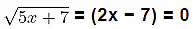
Squaring both sides of the equation we get,

Here, a = 4, b = −37 and c = 40
Substituting the value of a, b and c in the quadratic formula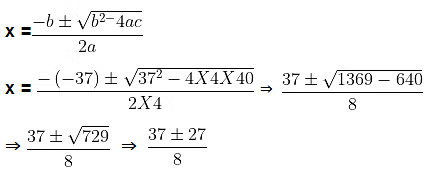

Taking +ve sign first,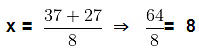

Taking -ve we get,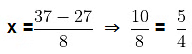

The roots of the given equation are 8 and 5/4.

Example 7: Find the numerical difference of the roots of the equation x² − 7x − 30 = 0
The given quadratic equation is x² − 7x − 30 = 0
Here a = 1, b = −7 and c = −30
Substituting the value of a, b and c in the quadratic formula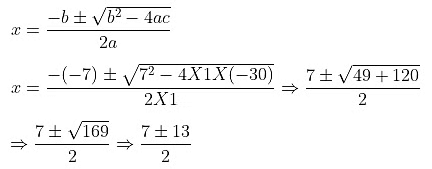

Taking +ve sign first,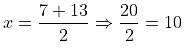

Taking -ve we get,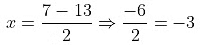

The two roots are 10 and -3
The difference of the roots= 10 − (−3) = 10 + 3 = 13

Example 8: Find the discriminant of the quadratic equation x² −4x − 5 = 0
The given quadratic equation is x² − 4x − 5 = 0.
On comparing with ax² + bx + c = 0 we get,
a = 1,b = −4, and c = −5

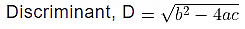
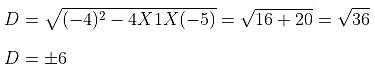
Example 9: Find the value of p, so that the quadratic equation px(x − 2) + 9 = 0 has equal roots.
The given quadratic equation is px(x − 2) + 9 = 0
px² − 2px + 9 = 0
Now comparing with ax² + bx + c = 0 we get,
a = p, b = −2p and c = 9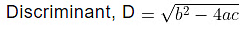

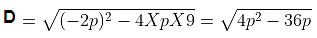
The given quadratic equation will have equal roots if D = 0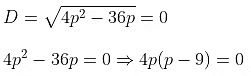

p = 0 and p − 9 = 0 ⇒ p = 9
p = 0 and p = 9
The value of p cannot be zero as the coefficient of x, (−2p) will become zero.
Therefore, we take the value of p = 9.

Example 10: If x = −1 is a root of the quadratic equations 2x² +px + 5 = 0 and the quadratic equation p(x² + x) + k = 0 has equal roots, then find the value of k.
The given quadratic equation is 2x² + px + 5 = 0. If x = −1 is the root of the equation then,
2(−1)2 + p(−1) + 5 = 0
2 − p + 5 = 0
⇒ −p = −7
p = 7
Putting the value of p in the equation p(x² + x) + k = 0,
7(x² + x) + k = 0
⇒ 7x² + 7x + k = 0
Now comparing with ax² + bx + c = 0 we get,
a = 7, b = 7 and c = k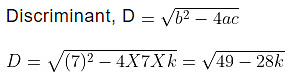

The given quadratic equation will have equal roots if D = 0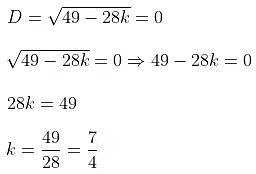

Therefore, the value of k is 7/4.

Solution of the Quadratic Equations by Completing the  Square (Deleted from NCERT Textbook)

If we have to find the solution of a quadratic equation by completing the square, we follow the steps given below.

The complete square is,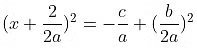

Example 11: Find the roots of the following quadratic equations by the method of completing the square:
(i) 2x² − 7x + 3 = 0
The given quadratic equation is 2x² − 7x + 3 = 0
The coefficient of x² is not 1, so we divide the whole equation by 2.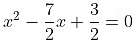

Now move 3/2 to RHS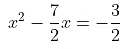

Adding (7/4)² to both sides we get,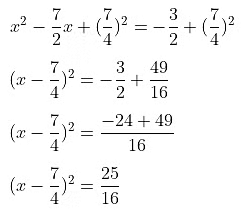

Taking square root of both sides we get,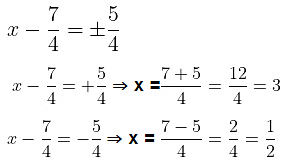

The roots of the equation are 3 and 1/2

(ii) 4x² + 4√3x + 3 = 0
Dividing the whole equation by 4, so that the coefficient of x² is 1.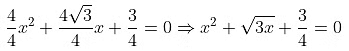

Shifting 3/4 to RHS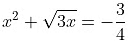

Adding 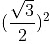 to both sides we get,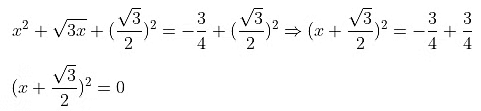

Taking the square root of both sides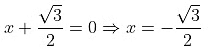

The roots of the given equation are

Example 12: Solve the quadratic equation

x² − (√5 + 1)x + √5 = 0 by completing the square method.
The given quadratic equation is, x² − (√5 + 1)x = −√5 = 0
Shifting √5 to RHS we get,
x² − (√5 + 1)x = −√5
Adding 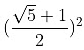 to both sides we get,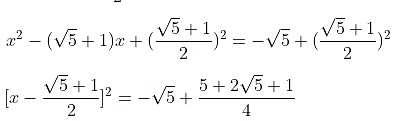

Taking +ve sign first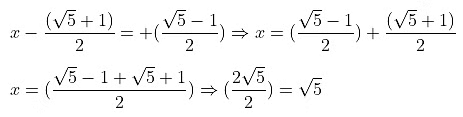

Taking –ve sign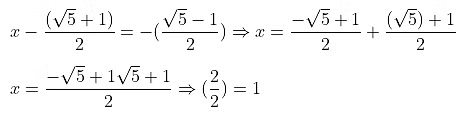

The roots of the given equation are √5 and 1