JEE Advance Previous Year Questions (2018 - 2024): Inverse Trigonometric Functions | Mathematics (Maths) for JEE Main & Advanced PDF Download
| Table of contents |

|
| JEE Advance PYQ 2024 |

|
| JEE Advance PYQ 2023 |

|
| JEE Advance PYQ 2022 |

|
| JEE Advance PYQ 2019 |

|
| JEE Advance PYQ 2018 |

|
JEE Advance PYQ 2024
Q1: Considering only the principal values of the inverse trigonometric functions, the value of
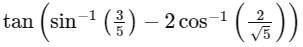 is
is
(a) 724
(b) -724
(c) -524
(d) 524 [JEE Advanced 2024 Paper 2]
Ans: (b)
= 9 - 1624 = -724
JEE Advance PYQ 2023
Q1: Let 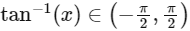 , for x ∈ R. Then the number of real solutions of the equation
, for x ∈ R. Then the number of real solutions of the equation 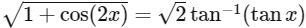 in the set
in the set 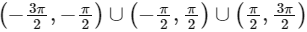 is equal to: [JEE Advanced 2023 Paper 1]
is equal to: [JEE Advanced 2023 Paper 1]
Ans: 3
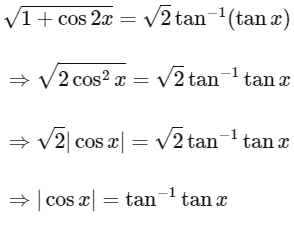

Number of solution = 3.
Q2: For any 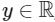 , let
, let 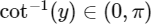 and
and 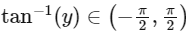 . Then the sum of all the solutions of the equation
. Then the sum of all the solutions of the equation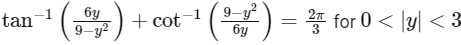 , is equal to : [JEE Advanced 2023 Paper 2]
, is equal to : [JEE Advanced 2023 Paper 2]
(a) 2√3 - 3
(b) 3 - 2√3
(c) 4√3 - 6
(d) 6 - 4√3
Ans: (c)
Concept :

Solution : Given, 0<|y|<3
⇒ y ∈ (−3, 3)− {0}
9 − y2 is always positive when y ∈ (−3, 3)− {0}
And 6y is positive when y ∈ (0, 3)
And 6y is negative when y ∈ (−3, 0)
∴ In overall, 6y / 9 − y2 > 0 when y ∈ (0, 3)
And 6y / 9 − y2 < 0 when y∈(−3, 0)
Case - 1 :
When -3 < y < 0
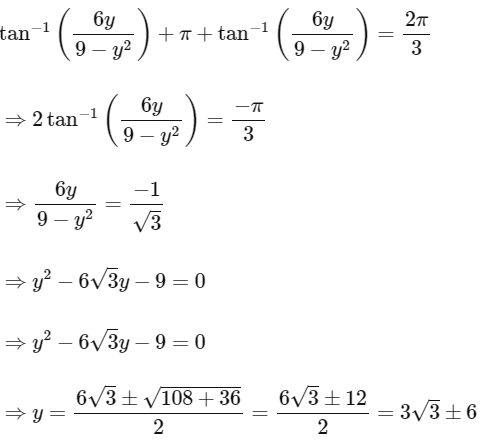
as, 
Case-2 : When 0 < y < 3
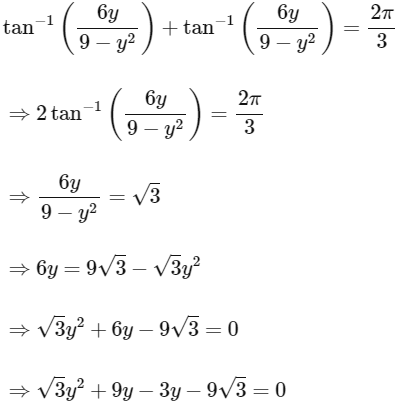
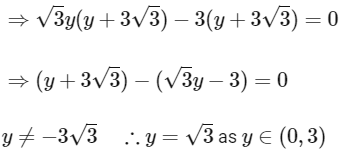
∴ Sum of solutions = 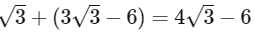
JEE Advance PYQ 2022
Q1: Considering only the principal values of the inverse trigonometric functions, the value of 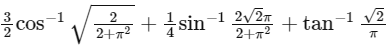 is [JEE Advanced 2022 Paper 1]
is [JEE Advanced 2022 Paper 1]Ans: 2.35 to 2.37
Given,
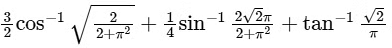
Let, 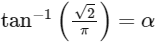

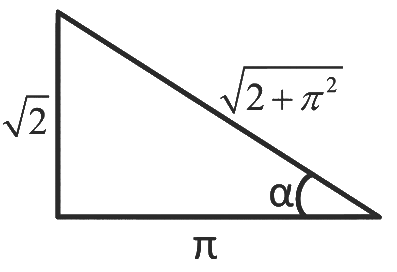 We know,
We know, 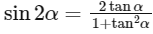
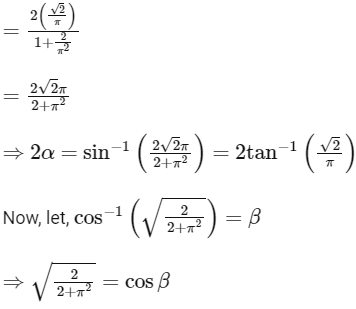
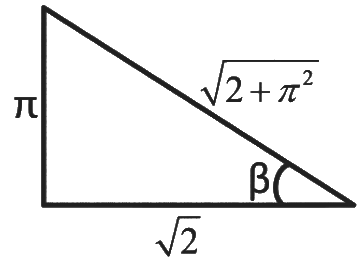

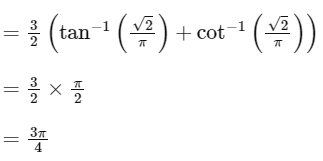
= 2.36
JEE Advance PYQ 2019
Q1: The value of 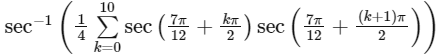 in the interval
in the interval 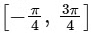 equals _________ [JEE Advanced 2019 Paper 2]
equals _________ [JEE Advanced 2019 Paper 2]Ans: 0
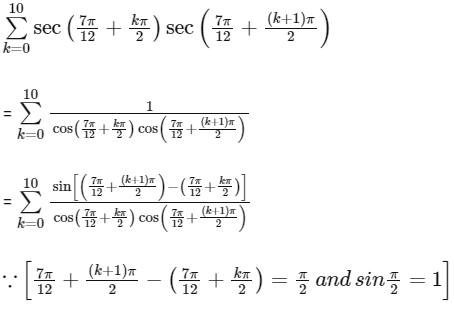
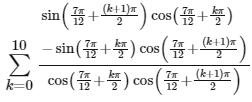
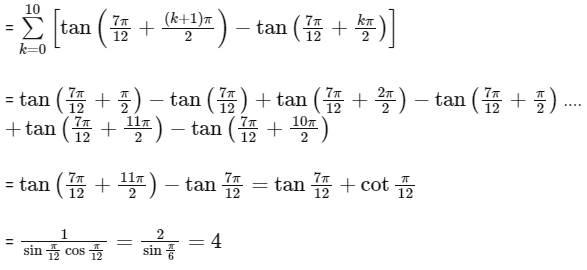
So, 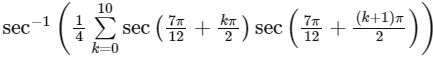
= sec−1 (1) = 0
Q2: For non-negative integers n, let
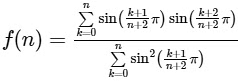
Assuming cos−1 x takes values in [0, π], which of the following options is/are correct?
(a) If α = tan(cos−1 f(6)), then α2 + 2α −1 = 0
(b) 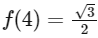
(c) sin(7 cos−1 f(5)) = 0
(d) 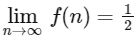 [JEE Advanced 2019 Paper 2]
[JEE Advanced 2019 Paper 2]
Ans: (a), (b) & (c)
It is given, that for non-negative integers 'n',
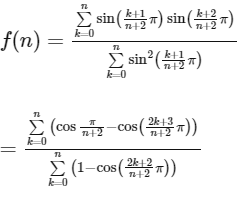
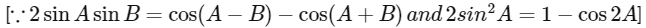
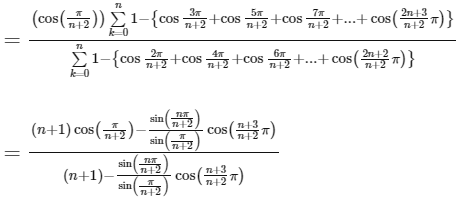
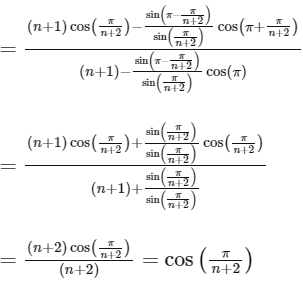
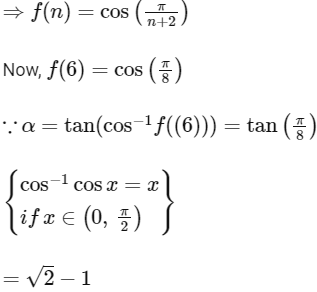
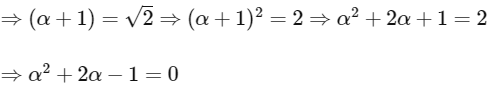
Now, 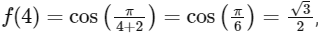
Now, 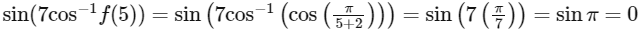 and Now,
and Now, 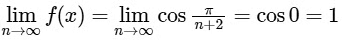
Hence, options (a), (b) and (c) are correct.
JEE Advance PYQ 2018
Q1: The number of real solutions of the equation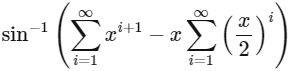
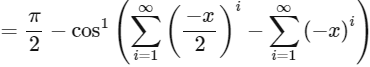 lying in the interval
lying in the interval 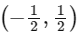 is ____________. (Here, the inverse trigonometric functions sin−1 x and cos−1 x assume values in [−π/2, π/2] and [0, π], respectively.) [JEE Advanced 2018 Paper 1]
is ____________. (Here, the inverse trigonometric functions sin−1 x and cos−1 x assume values in [−π/2, π/2] and [0, π], respectively.) [JEE Advanced 2018 Paper 1]
Ans: 2
We have,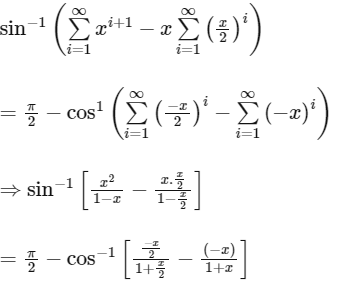
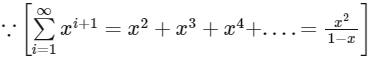 using sum of infinite terms of GP
using sum of infinite terms of GP
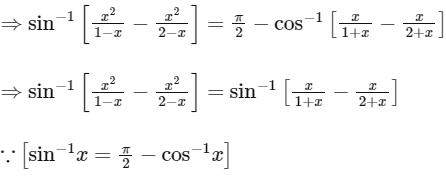
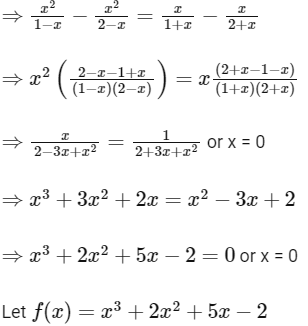
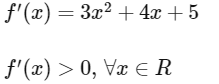
∴ x3 + 2x2 + 5x - 2 has only one real roots
Therefore, total number of real solution is 2.
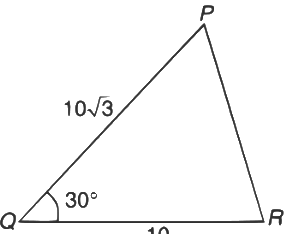
Q2: In a ΔPQR = 30∘ and the sides PQ and QR have lengths 10√3 and 10, respectively. Then, which of the following statement(s) is(are) TRUE?
(a) ∠QPR = 45∘
(b) The area of the ΔPQR is 25√3 and ∠QRP = 120∘
(c) The radius of the incircle of the ΔPQR is 10√3 − 15
(d) The area of the circumcircle of the ΔPQR is 100π [JEE Advanced 2018 Paper 1]
Ans: (b), (c) & (d)
We have,
In ΔPQR
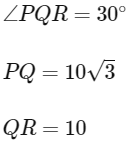
By cosine rule
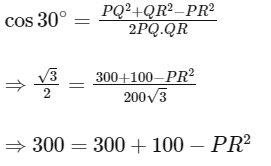
⇒ PR = 10
Since, PR = QR = 10
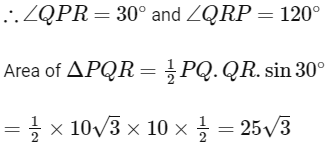
Radius of incircle of

and radius of circumcircle
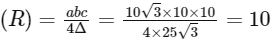
∴ Area of circumcircle of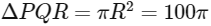
Hence, option (b), (c) and (d) are correct answer.
|
209 videos|447 docs|187 tests
|
FAQs on JEE Advance Previous Year Questions (2018 - 2024): Inverse Trigonometric Functions - Mathematics (Maths) for JEE Main & Advanced
| 1. What are the important properties of inverse trigonometric functions that I should know for JEE Advance? |  |
| 2. How can I effectively prepare for inverse trigonometric functions in JEE Advance? |  |
| 3. Are there any common mistakes to avoid while solving problems on inverse trigonometric functions in JEE? |  |
| 4. What types of questions related to inverse trigonometric functions are typically asked in JEE Advance? |  |
| 5. How do inverse trigonometric functions relate to calculus in JEE Advance? |  |
|
209 videos|447 docs|187 tests
|




















