JEE Advanced Previous Year Questions (2018 - 2024): Limits, Continuity and Differentiability | Mathematics (Maths) for JEE Main & Advanced PDF Download
2024
Q1: Let k ∈ ℝ. If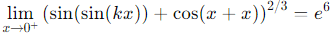 then the value of k is:
then the value of k is:(a) 1
(b) 2
(c) 3
(d) 4 [JEE Advanced 2024 Paper 2]
Ans: (b)
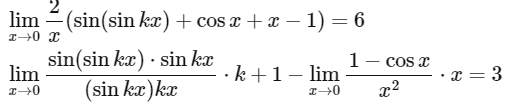
k + 1 = 3 ⇒ k = 2
Q2: Let f : ℝ → ℝ be a function defined by
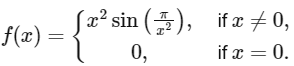
Then which of the following statements is TRUE?
(a) f(x) = 0 has infinitely many solutions in the interval [1/10¹⁰, ∞).
(b) f(x) = 0 has no solutions in the interval [1/π, ∞).
(c) The set of solutions of f(x) = 0 in the interval (0, 1/10¹⁰) is finite.
(d) f(x) = 0 has more than 25 solutions in the interval (1/π², 1/π). [JEE Advanced 2024 Paper 2]
Ans: (d)
Option-A: f(x) = x² sin(π/x²)
f(x) = 0 ⇒ sin(π/x²) = 0 ⇒ π/x² = nπ, n ∈ ℕ
x² = 1/n ⇒ x = 1/√n
1/√n ≥ 1/10¹⁰ ⇒ √n ≥ 10¹⁰ ⇒ n ≤ 10²⁰, finite number of solutions.
Option-B: x = 1/√n
1/√n > 1/π ⇒ x > √n ⇒ n < π², Number of solutions is 9.
Option-C: x = 1/√n
1/√n < 1/10¹⁰ ⇒ √n > 10¹⁰ ⇒ n > 10²⁰, infinite number of solutions.
Option-D: 1/π² < 1/√n < 1/π ⇒ √n ∈ (π, π²) ⇒ n ∈ (π², π⁴), Definitely more than 25 solutions.
Q3: Let f : ℝ → ℝ and g : ℝ → ℝ be functions defined by
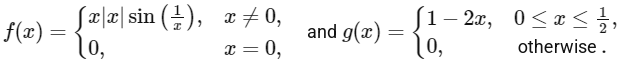
Let a, b, c, d ∈ ℝ. Define the function h : ℝ → ℝ by
h(x) = a f(x) + b (g(x) + g(1/2 - x)) + c(x - g(x)) + d g(x), x ∈ ℝ.
Match each entry in List-I to the correct entry in List-II.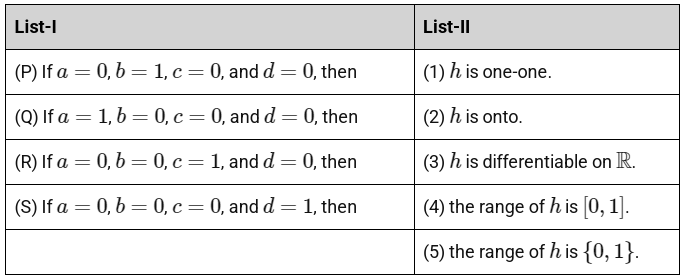
The correct option is:
(a) (P) → (4), (Q) → (3), (R) → (1), (S) → (2)
(b) (P) → (5), (Q) → (2), (R) → (4), (S) → (3)
(c) (P) → (5), (Q) → (3), (R) → (2), (S) → (4)
(d) (P) → (4), (Q) → (2), (R) → (1), (S) → (3) [JEE Advanced 2024 Paper 1 ]
Ans: (c)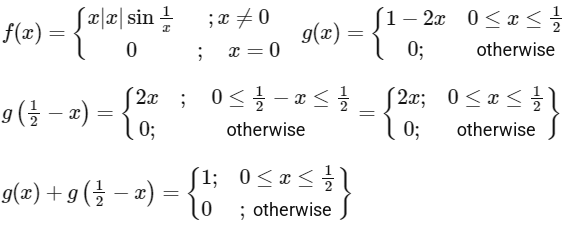
(P) Now a = 0, b = 1, c = 0, d = 0.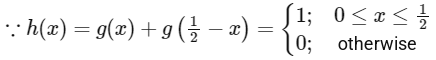
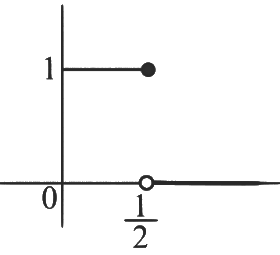 Hence Range of h(x) is {0, 1}
Hence Range of h(x) is {0, 1}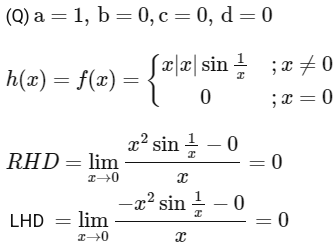
Hence h(x) 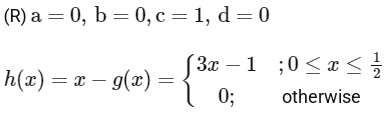

 Range of h(x) is [0, 1]
Range of h(x) is [0, 1]
Q4: Let S be the set of all (α, β) ∈ ℝ × ℝ such that

Then which of the following is (are) correct?
(a) (-1, 3) ∈ S
(b) (-1, 1) ∈ S
(c) (1, -1) ∈ S
(d) (1, -2) ∈ S [JEE Advanced 2024 Paper 2]
Ans: (b), (c)
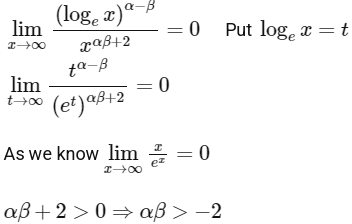
2023
Q1: Let f : (0, 1)→ R be the function defined as
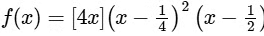 , where [x] denotes the greatest integer less than or equal to x. Then which of the following statements is(are) true?(a) The function f is discontinuous exactly at one point in (0, 1)
, where [x] denotes the greatest integer less than or equal to x. Then which of the following statements is(are) true?(a) The function f is discontinuous exactly at one point in (0, 1)(b) There is exactly one point in (0, 1) at which the function f is continuous but NOT differentiable
(c) The function f is NOT differentiable at more than three points in (0, 1)
(d) The minimum value of the function f is -1/512 [JEE Advanced 2023 Paper 2]
Ans: (a) & (b)
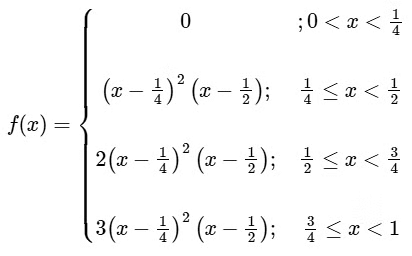
f (x) is discontinuous at x = 3/4 only
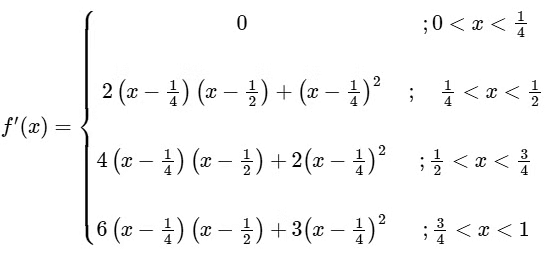
f (x) is non-differentiable at x = 1/2 and 3/4
Minimum values of f(x) occur at x = 5/12 whose value is -1/432
2022
Q1: For positive integer n, define
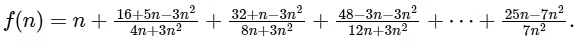
Then, the value of 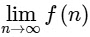 is equal to :
is equal to :
(a) 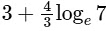
(b) 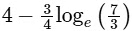
(c) 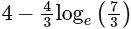
(d) 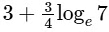 [JEE Advanced 2022 Paper 2]
[JEE Advanced 2022 Paper 2]
Ans: (b)
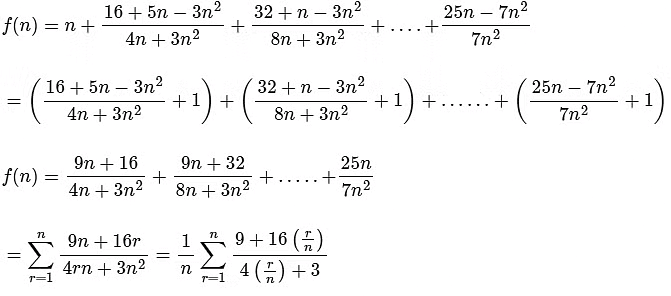
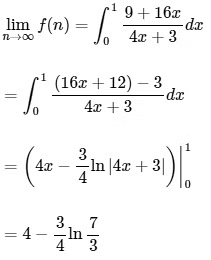
Q2: If 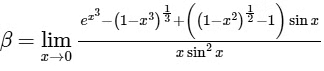 , then the value of 6β is ___________. [JEE Advanced 2022 Paper 2]
, then the value of 6β is ___________. [JEE Advanced 2022 Paper 2]
Ans: 5
Given,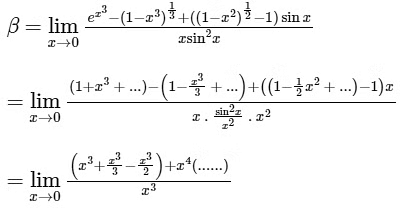
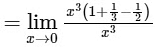 [Neglecting higher power of x]
[Neglecting higher power of x]
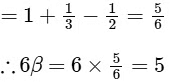
Q3: Let α be a positive real number. Let 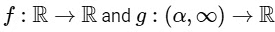 be the functions defined by
be the functions defined by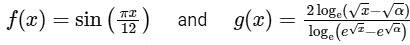
Then the value of 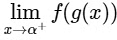 is_______. [JEE Advanced 2022 Paper 1]
is_______. [JEE Advanced 2022 Paper 1]
Ans: 0.49 to 0.51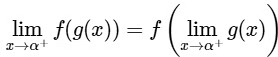 [As f(x) is continuous function so we can write this]
[As f(x) is continuous function so we can write this]
Now,
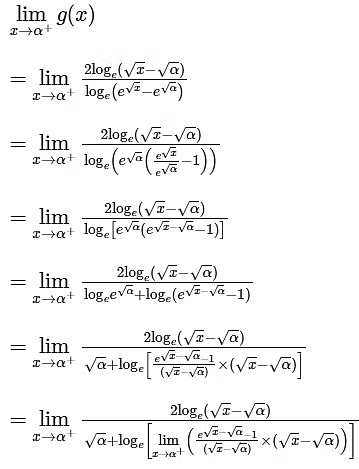
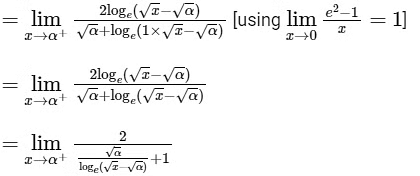
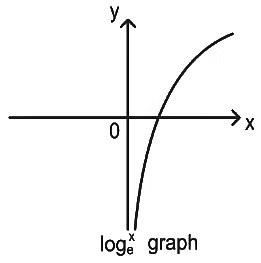
From graph you can see 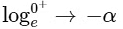
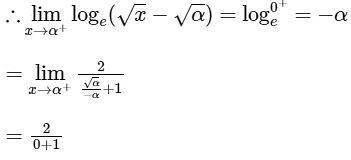
= 2
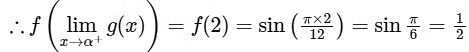
2021
Q1: Let f : R → R be defined by
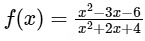 Then which of the following statements is (are) TRUE?
Then which of the following statements is (are) TRUE?(a) f is decreasing in the interval (−2, −1)
(b) f is increasing in the interval (1, 2)
(c) f is onto
(d) Range of f is [−3/2, 2] [JEE Advanced 2021 Paper 1]
Ans: (a) & (b)
Given,
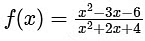 ---- (i)
---- (i)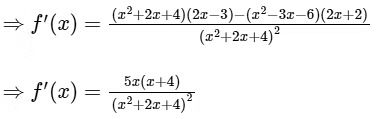

Sign scheme for f'(x)
Here, f is decreasing in the interval (−2, −1) and f is increasing in the interval (1, 2).
Now, 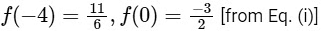 and
and 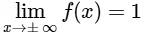
∴ Range = 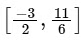
Hence, f(x) is into.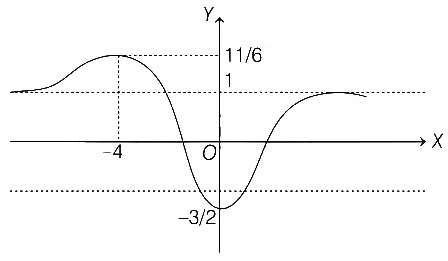 f(x) has local maxima at x = −4
f(x) has local maxima at x = −4
and local minima at x = 0.
2020
Q1: Let f : R → R and g : R → R be functions satisfying f(x + y) = f(x) + f(y) + f(x)f(y)
and f(x) = xg(x) for all x, y ∈ R.
If 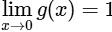 , then which of the following statements is/are TRUE?
, then which of the following statements is/are TRUE?
(a) f is differentiable at every x∈R
(b) If g(0) = 1, then g is differentiable at every x ∈ R
(c) The derivative f'(1) is equal to 1
(d) The derivative f'(0) is equal to 1 [JEE Advanced 2020 Paper 2]
Ans: (a), (b) & (d)
The given function f : R → R is satisfying as
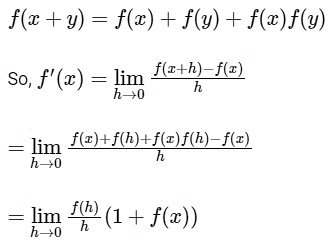
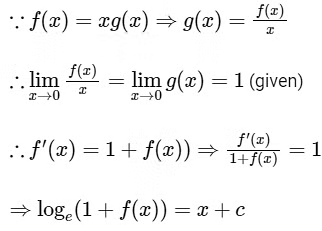
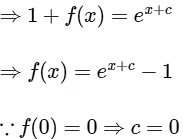
Therefore, f(x) = ex − 1 is differentiable at every x ∈ R.
and 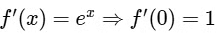 Now,
Now, 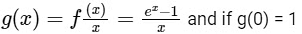
LHD (at x = 0) of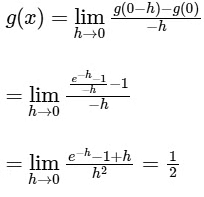
and, RHD (at x = 0) of
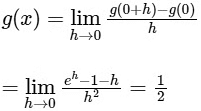
So, if g(0) = 1, then g is differentiable at every x ∈ R.
Q2: Let the function f : R → R be defined by f(x) = x3 − x2 + (x − 1)sin x and let g : R → R be an arbitrary function. Let fg : R → R be the product function defined by (fg)(x) = f(x)g(x). Then which of the following statements is/are TRUE?
(a) If g is continuous at x = 1, then fg is differentiable at x = 1
(b) If f g is differentiable at x = 1, then g is continuous at x = 1
(c) If g is differentiable at x = 1, then fg is differentiable at x = 1
(d) If f g is differentiable at x = 1, then g is differentiable at x = 1 [JEE Advanced 2020 Paper 1]
Ans: (a) & (c)
Given functions f : R → R be defined
by f(x) = x3 − x2 + (x + 1) sin x and g : R → R be an arbitrary function.
Now, let g is continuous at x = 1, then
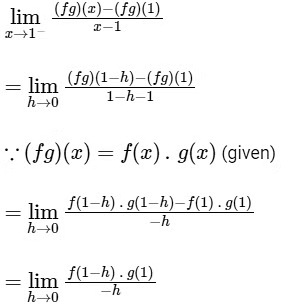
{∵ f(1) = 0 and g is continuous at x = 1, so g(1 − h) = g(1)}
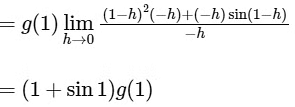
Similarly, 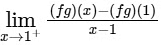

∵ RHD and LHD of function fg at x = 1 is finitely exists and equal, so fg is differentiable at x = 1
Now, let (fg)(x) is differentiable at x = 1, so
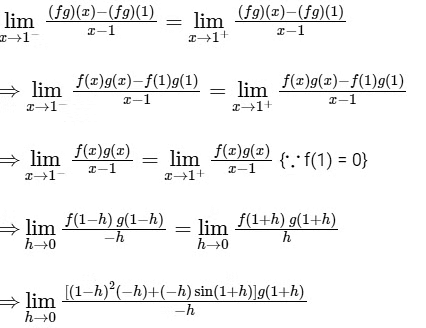

It does not mean that g(x) is continuous or differentiable at x = 1.
But if g is differentiable at x = 1, then it must be continuous at x = 1 and so fg is differentiable at x = 1.
Q3: The value of the limit 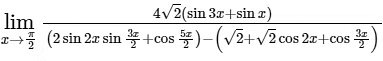 is ________. [JEE Advanced 2020 Paper 2]Ans: 8
is ________. [JEE Advanced 2020 Paper 2]Ans: 8
The Limit
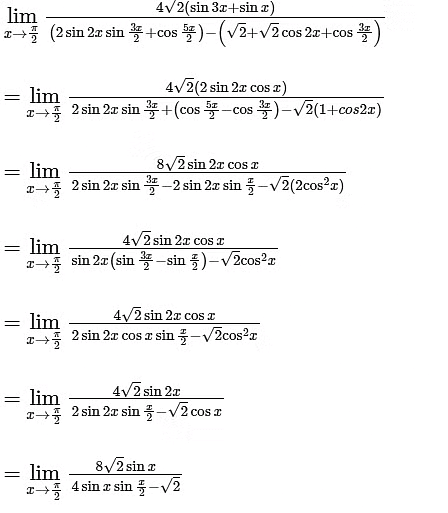
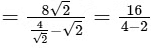
= 8
Q4: let e denote the base of the natural logarithm. The value of the real number a for which the right hand limit 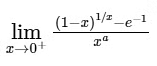 is equal to a non-zero real number, is ____ . [JEE Advanced 2020 Paper 1]
is equal to a non-zero real number, is ____ . [JEE Advanced 2020 Paper 1]
Ans: 1
The right hand limit
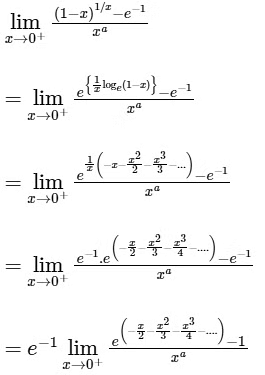
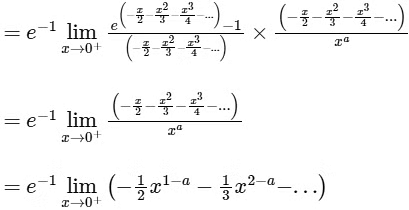
The above limit will be non-zero, if a = 1. And at a = 1, the value of the limit is

2019
Q1: For a ∈ R, |a| > 1, let
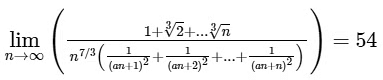
(a) -6
(b) -7
(c) 8
(d) -9 [JEE Advanced 2019 Paper 2]
Ans: (c) & (d)
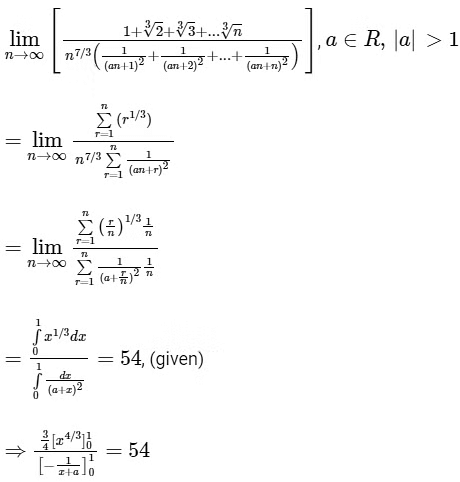
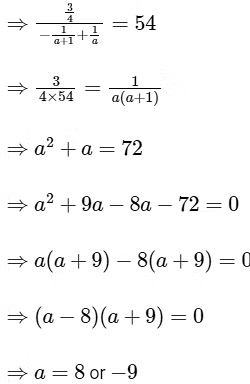
Hence, options (c) and (d) are correct.
Q2: Let f : R → R be given by
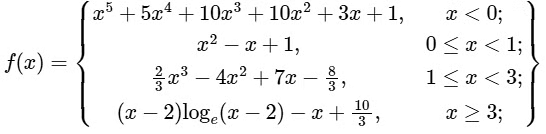
(a) f is increasing on (−∞, 0)
(b) f' is not differentiable at x = 1
(c) f is onto
(d) f' has a local maximum at x = 1 [JEE Advanced 2019 Paper 1]
Ans: (b), (c) & (d)
Given function f : R → R is
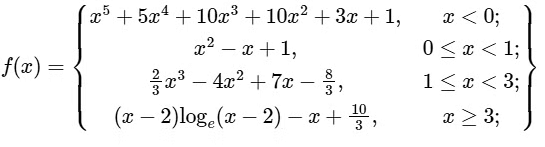
So,
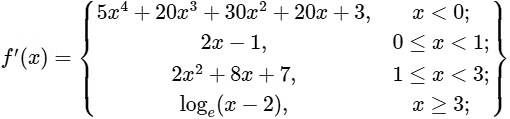
At x = 1, f"(1-) = 2 > 0 and f"(1+) = 4−8 = −4 < 0
∴ f'(x) is not differentiable at x = 1 and f'(x) has a local maximum at x = 1.
For x ∈ (−∞, 0)
f'(x) = 5x4 + 20x3 + 30x2 + 20x + 3
and since
f'(−1) = 5−20 + 20 + 30 − 20 + 3 = −2 < 0
So, f(x) is not increasing on x ∈(−∞, 0).
Now, as the range of function f(x) is R, so f is onto function.
Hence, options (b), (c) and (d) are correct.
2018
Q1: For every twice differentiable function f : R → [−2, 2] with (f(0))2 + (f′(0))2 = 85, which of the following statement(s) is(are) TRUE?
(a) There exist r, s ∈ R, where r < s, such that f is one-one on the open interval (r, s)
(b) There exists x0 ∈ (−4, 0) such that |f'(x0)| ≤ 1
(c)
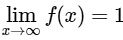 (d) There exists α ∈ (−4, 4) such that f(α) + f"(α) = 0 and f'(α) ≠ 0 [JEE Advanced 2018 Paper 1]Ans: (a), (b) & (d)
(d) There exists α ∈ (−4, 4) such that f(α) + f"(α) = 0 and f'(α) ≠ 0 [JEE Advanced 2018 Paper 1]Ans: (a), (b) & (d)We have,
(f(0))2 + (f′(0))2 = 85
and f : R → [−2, 2]
(a) Since, f is twice differentiable function, so f is continuous function.
∴ This is true for every continuous function.
Hence, we can always find x ∈ (r, s), where f(x) is one-one.
∴ This statement is true.
(b) By L.M.V.T.
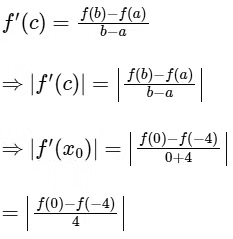
Range of f is [−2, 2]
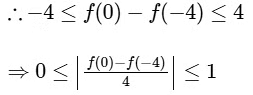
Hence, |f'(x0)| = 1.
Hence, statement is true.
(c) As no function is given, then we assume
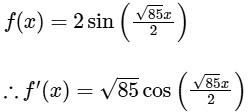
Now, 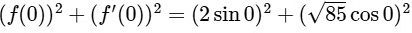
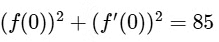
and 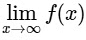 does not exists.Hence, statement is false.
does not exists.Hence, statement is false.
(d) From option b, 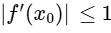
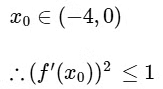
hence, 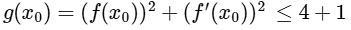
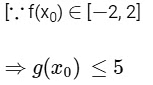
Now, let p ∈ (−4, 0) for which g(p) = 5
Similarly, let q be smallest positive number q ∈ (0, 4)
such that g(q) = 5
Hence, by Rolle's theorem is (p, q)
g'(c) = 0 for α ∈ (−4, 4) and since g(x) is greater than 5 as we move from x = p to x = q
and f(x))2 ≤ 4
⇒ (f'(x))2 ≥ 1 in (p, q)
Thus, g'(c) = 0
⇒ f'f + f'f" = 0
So, f(α) + f"(α) = 0 and f'(α) ≠ 0
Hence, statement is true.
Q2: Let f : R → R and g : R → R be two non-constant differentiable functions. If f'(x) = (e(f(x) − g(x))) g'(x) for all x ∈ R and f(1) = g(2) = 1, then which of the following statement(s) is (are) TRUE?
(a) f(2) < 1 − loge2
(b) f(2) > 1 − loge2
(c) g(1) > 1 − loge2
(d) g(1) < 1 − loge2 [JEE Advanced 2018 Paper 1]
Ans: (b) & (c)
We have,
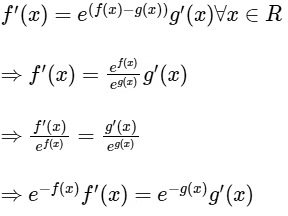
On integrating both side, we get

At x = 1
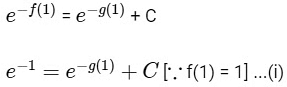
At x = 2
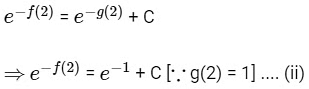
From Eqs. (i) and (ii)
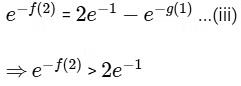
We know that, e−x is decreasing
∴ −f(2) < loge 2−1
f(2) > 1 − loge 2
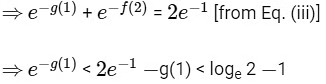 ⇒ g(1) > −loge 2
⇒ g(1) > −loge 2
Q3: Let 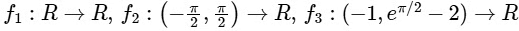 and
and  be functions defined by
be functions defined by
(i) 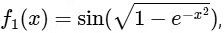
(ii) 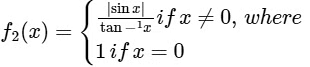 the inverse trigonometric function tan−1x assumes values in (-π/2, π/2)
the inverse trigonometric function tan−1x assumes values in (-π/2, π/2)
(iii) 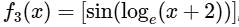 , where for t ∈ R, [t] denotes the greatest integer less than or equal to t,
, where for t ∈ R, [t] denotes the greatest integer less than or equal to t,
(iv) 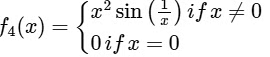

(b) P → 4 ; Q → 1 ; R → 2 ; S → 3
(c) P → 4 ; Q → 2 ; R → 1 ; S → 3
(d) P → 2 ; Q → 1 ; R → 4 ; S → 3 [JEE Advanced 2018 Paper 2 ]
Ans: (d)
(i) Given,
f1 : R → R and f1(x) =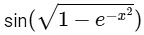
∴ f1(x) is continuous at x = 0
Now,
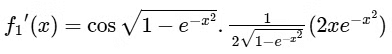
At x = 0
f1'(x) does not exists.
∴ f1(x) is not differential at x = 0
Hence, option (2) for P.
(ii) Given, 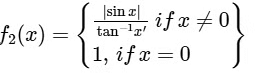
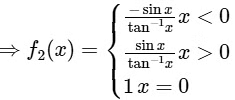
Clearly, f2(x) is not continuous at x = 0.
∴ Option (1) for Q.
(iii) Given, f3(x) = [sin(loge(x + 2))], where [ ] is G.I.F.
and f3 : (−1, eπ/2 − 2) → R
It is given,
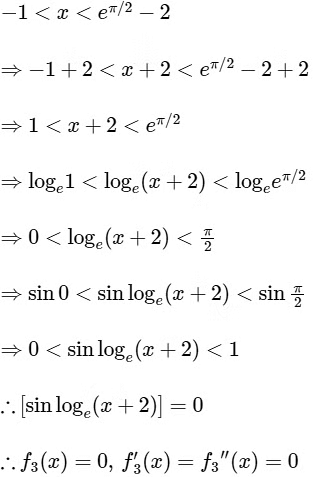
It is differentiable and continuous at x = 0.
∴ Option (4) for R
(iv) Given, 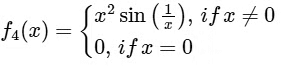
Now, 
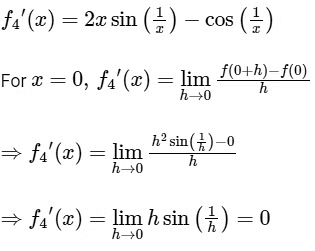
thus
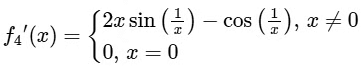
Again, 
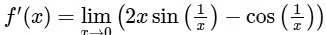 does not exists.
does not exists.
Since,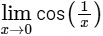 does not exists.
does not exists.
Hence, f'(x) is not continuous at x = 0.
∴ Option (3) for S.
Q4: The value of 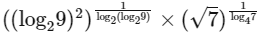 is ________. [JEE Advanced 2018 Paper 1]
is ________. [JEE Advanced 2018 Paper 1]
Ans: 8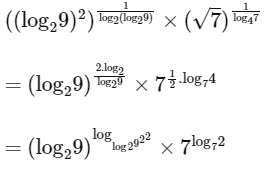
= 22 x 2
= 8
|
209 videos|467 docs|187 tests
|
FAQs on JEE Advanced Previous Year Questions (2018 - 2024): Limits, Continuity and Differentiability - Mathematics (Maths) for JEE Main & Advanced
| 1. What are the key topics covered in Limits, Continuity, and Differentiability for JEE Advanced? |  |
| 2. How can I effectively prepare for Limits, Continuity, and Differentiability in the JEE Advanced exam? |  |
| 3. What are some common types of problems asked in the JEE Advanced from Limits and Continuity? |  |
| 4. How important is the topic of Differentiability in the JEE Advanced exam? |  |
| 5. Are there any specific strategies for tackling limits and continuity questions in JEE Advanced? |  |






















