JEE Advanced Previous Year Questions (2018 - 2024): Differential Equations | Mathematics (Maths) for JEE Main & Advanced PDF Download
2024
Q1: Let f(x) be a continuously differentiable function on the interval (0, ∞) such that f(1) = 2 and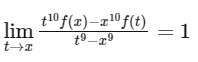 for each x > 0. Then, for all x > 0, f(x) is equal to:
for each x > 0. Then, for all x > 0, f(x) is equal to:
(a) 3111x - 911 x¹⁰
(b) 911x + 1311 x¹⁰
(c) -911x + 3111 x¹⁰
(d) 1311x + 911 x¹⁰ [JEE Advanced 2024 Paper 1]
Ans: (b)
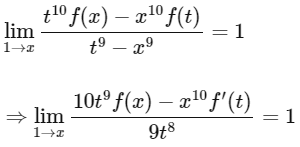
⇒ 10x f(x) - x² f'(x) = 9
⇒ x² f'(x) = 10x f(x) - 9
⇒ f'(x) = 10 f(x)x - 9x²
⇒ dydx - 10x y = - 9x²
⇒ yx¹⁰ = 911x¹¹ + c
∴ f(1) = 2 ⇒ 21 = 911 + c ⇒ c = 1311
∴ f(x) = 911x + 1311 x¹⁰
⇒ Option (B) is correct.
2023
Q1: For x ∈ R, let g(x) be a solution of the differential equation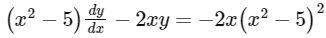 such that y(2) = 7. Then the maximum value of the function y(x) is : [JEE Advanced 2023 Paper 2]
such that y(2) = 7. Then the maximum value of the function y(x) is : [JEE Advanced 2023 Paper 2]
Ans: 16
Q2: Let 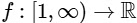 be a differentiable function such that f(1) = 1/3 and
be a differentiable function such that f(1) = 1/3 and 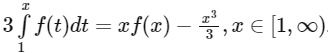 . Let e denote the base of the natural logarithm. Then the value of f(e) is :
. Let e denote the base of the natural logarithm. Then the value of f(e) is :
(a) 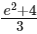
(b) 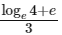
(c) 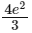
(d) 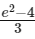 [JEE Advanced 2023 Paper 2]
[JEE Advanced 2023 Paper 2]
Ans: (c)
1. We are given a relationship between the integral of the function f(t) and the function f(x) :
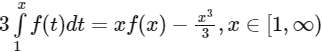
2. Differentiate both sides of the above equation with respect to x :
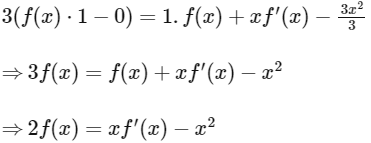
3. We can rewrite this as a first order linear differential equation:
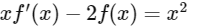
4. The general form of a first order linear differential equation is:
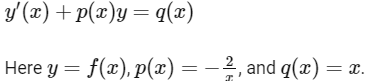
5. The integrating factor is obtained by exponentiating the integral of p(x) with respect to x:
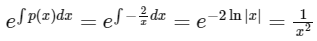
6. ∴ Solution of D.E :
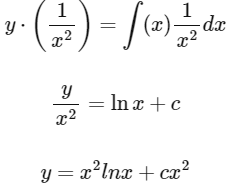
∴ The general solution is :
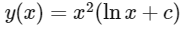
Here, y(x) is the same as f(x), i.e. the function we're trying to find.
7. Given that f(1) = 1 / 3, let's use this condition to find the constant c :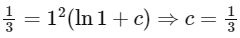
Therefore, the function f(x) we are looking for is:
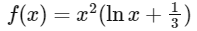
We want to find f(e), so substituting x = e into the function, we get :
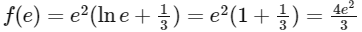
So, the correct answer is Option C.
2022
Q1: If y(x) is the solution of the differential equation 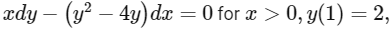 and the slope of the curve y = y(x) is never zero, then the value of 10y(√2) is: [JEE Advanced 2022 Paper 2]
and the slope of the curve y = y(x) is never zero, then the value of 10y(√2) is: [JEE Advanced 2022 Paper 2]
Ans: 8
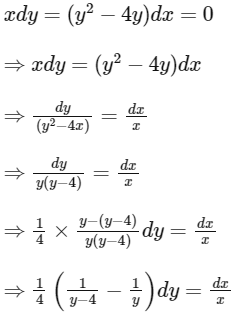
Integrating both side, we get
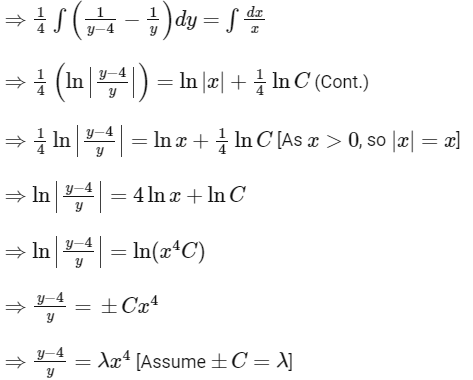
Given, y (1) = 2
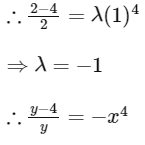
Now, 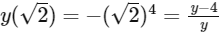
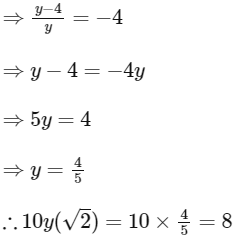
Q2: For x ∈ R, let the function y(x) be the solution of the differential equation
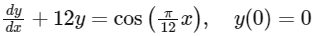
Then, which of the following statements is/are TRUE ?
(a) y(x) is an increasing function
(b) y(x) is a decreasing function
(c) There exists a real number β such that the line y = β intersects the curve y = y(x) at infinitely many points
(d) y(x) is a periodic function [JEE Advanced 2022 Paper 2]
Ans: (c)
Given, 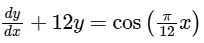
This is a linear differential equation.
Where P = 12 and 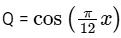
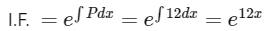
Solution of differencial equation is
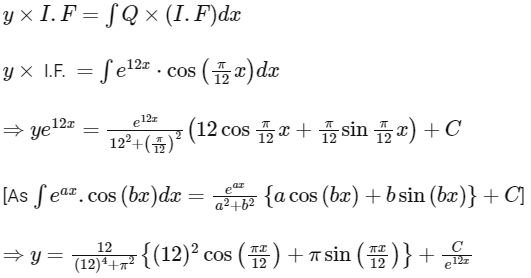
Given, y(0) = 0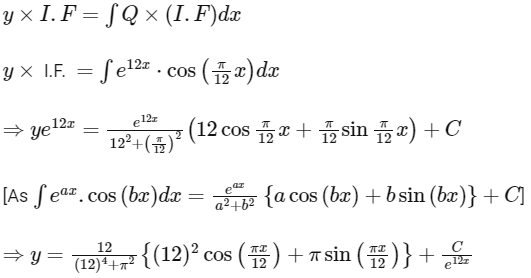
y(x) is not a periodic function as e−12x is a non-periodic function.
∴ Option (D) is a wrong statement.
Now, 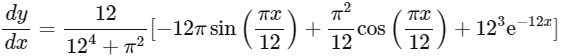
Values of 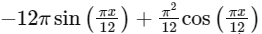 varies between
varies between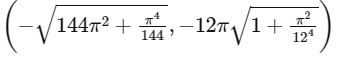
So, f(x) is neither increasing nor decreasing.
∴ Option (A) and (B) are wrong statements.
For some β ∈ R, y = β intersects y = f(x) at infinitely many points.
So option C is correct.
2019
Q1: Let Γ denote a curve y = y(x) which is in the first quadrant and let the point (1, 0) lie on it. Let the tangent to I` at a point P intersect the y-axis at YP. If PYP has length 1 for each point P on I`, then which of the following options is/are correct?
(a) 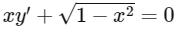
(b) 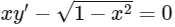
(c) 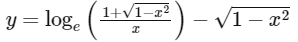
(d) 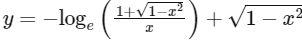
Ans: (a) & (c)
Let a point P(h, k) on the curve y = y(x), so equation of tangent to the curve at point P is
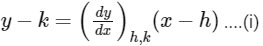
Now, the tangent (i) intersect the Y-axis at Yp, so coordinates Yp is 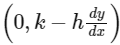
Where, 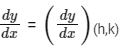
So, PYp = 1 (given)
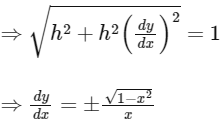
[on replacing h by x]
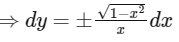
On putting x = sinθ, dx = cosθdθ, we get
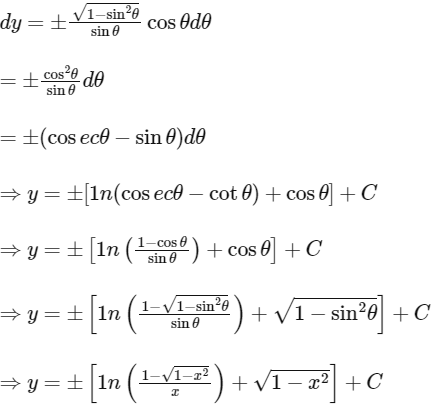
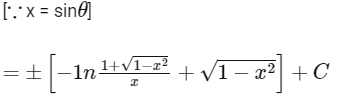
[on rationalization]
∵ The curve is in the first quadrant so y must be positive, so
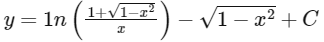
As curve passes through (1, 0), so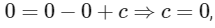 so required curve is
so required curve is
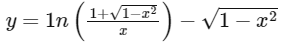
and required differential equation is
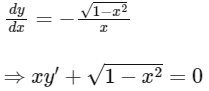
Hence, options (a) and (c) are correct.
2018
Q1: Let f : R → R be a differentiable function with f(0) = 0. If y = f(x) satisfies the differential equation 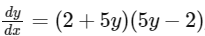 , then the value of
, then the value of 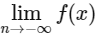 is [JEE Advanced 2018 Paper 2]
is [JEE Advanced 2018 Paper 2]
Ans: 0.4
We have,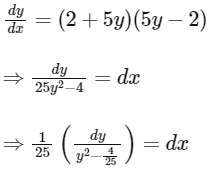
On integrating both sides, we get
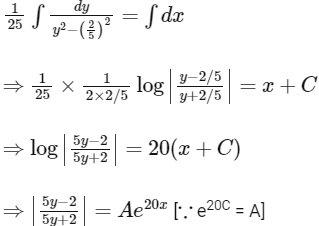
when x = 0 ⇒ y = 0, then A = 1
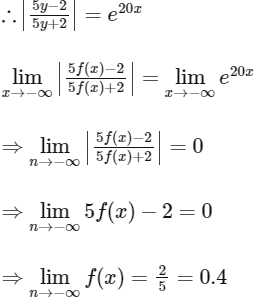
|
177 videos|590 docs|160 tests
|
















