JEE Advanced Previous Year Questions (2018 - 2024): Wave Optics | Physics for JEE Main & Advanced PDF Download
2024
Q1: In a Young's double slit experiment, each of the two slits A and B, as shown in the figure, are oscillating about their fixed center and with a mean separation of 0.8 mm. The distance between the slits at time t is given by d = (0.8 + 0.04 sin ωt) mm, where ω = 0.08 rads⁻¹. The distance of the screen from the slits is 1 m and the wavelength of the light used to illuminate the slits is 6000 Å. The interference pattern on the screen changes with time, while the central bright fringe (zeroth fringe) remains fixed at point O.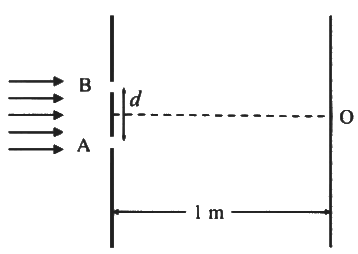 The 8th bright fringe above the point O oscillates with time between two extreme positions. The separation between these two extreme positions, in micrometer (μm), is ______. [JEE Advanced 2024 Paper 2]
The 8th bright fringe above the point O oscillates with time between two extreme positions. The separation between these two extreme positions, in micrometer (μm), is ______. [JEE Advanced 2024 Paper 2]
Ans: 601.50
y = n λDd
For 8th fringe:
y = 8 λDd
ymax = 8 λDdmin
ymin = 8 λDdmax
ymax - ymin = 8 λD [1dmin - 1dmax]
Given values:
λ = 6000 Å
D = 1 m
dmax = 0.34 mm
dmin = 0.76 mm
ymax - ymin = 8 × 6000 × 10-10 × 1 [10.76 × 10-3 - 10.84 × 10-3]
= 8 × 6 × 10-4 × 0.080.76 × 0.84
= 601.5 μm
Q2: In a Young's double slit experiment, each of the two slits A and B, as shown in the figure, are oscillating about their fixed center and with a mean separation of 0.8 mm. The distance between the slits at time t is given by d = (0.8 + 0.04 sin ωt) mm, where ω = 0.08 rads⁻¹. The distance of the screen from the slits is 1 m and the wavelength of the light used to illuminate the slits is 6000 Å. The interference pattern on the screen changes with time, while the central bright fringe (zeroth fringe) remains fixed at point O.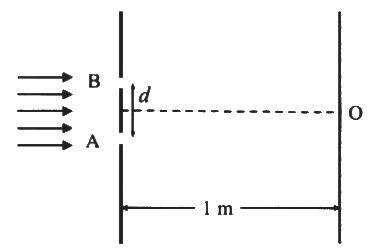 The maximum speed in μm/s at which the th 8th bright fringe will move is ______. [JEE Advanced 2024 Paper 2]
The maximum speed in μm/s at which the th 8th bright fringe will move is ______. [JEE Advanced 2024 Paper 2]
Ans: 24
y = n ⋅ λDd
v = dydt = -n ⋅ λ ⋅ dd² ⋅ d(d)dt
d = 0.8 + 0.04 sin(ωt)
d(d)dt = 0.04 ω cos(ωt)
For v → max ⇒ d(d)dt → max
For d(d)dt → max
cos(ωt) = 1 ⇒ sin(ωt) = 0
⇒ d(d)dt max = 0.04
⇒ d = 0.8 mm
vmax = 8 × 6000 × 10-10 × 1 × 0.04 × 0.080.8 × 0.8 × 10-6 × 10-3
= 24 μm/s
Q3: A point source S emits unpolarized light uniformly in all directions. At two points A and B, the ratio r = I_A / I_B of the intensities of light is 2. If a set of two polaroids having 45° angle between their pass-axes is placed just before point B, then the new value of r will be ______. [JEE Advanced 2024 Paper 1]
Ans: 8
To solve this problem, we start by understanding the information given and how the polarization of light affects light intensity.
Initially, we have the ratio of the intensities at points A and B given as:
r = IAIB = 2
This means:
IA = 2IB
Now, we place two polaroids with their pass-axes at an angle of 45° between them before point B. When unpolarized light passes through the first polaroid, it gets polarized, and its intensity is reduced to half of its original value:
IB1 = 12 IB
Here, IB1 is the intensity of light after passing through the first polaroid.
Next, this polarized light passes through the second polaroid, which is at an angle of 45° to the first one. According to Malus’s law, the intensity of light after passing through the second polaroid is given by:
IB2 = IB1 cos²(45°)
We know that:
cos(45°) = 1√2
Thus,
IB2 = 12 IB 1√2 2 = 12 IB × 12 = 14 IB
Now, the new intensity at point B is IB2. We need to calculate the new ratio r' of the intensities at points A and B:
r' = IAIB2
Substituting the values IA = 2IB and IB2 = 14 IB, we get:
r' = 2IB14 IB = 2 × 4 = 8
Therefore, the new value of r will be: r' = 8
2022
Q1: A double slit setup is shown in the figure. One of the slits is in medium 2 of refractive index n2. The other slit is at the interface of this medium with another medium 1 of refractive index n1( ≠ n2). The line joining the slits is perpendicular to the interface and the distance between the slits is d. The slit widths are much smaller than d. A monochromatic parallel beam of light is incident on the slits from medium 1. A detector is placed in medium 2 at a large distance from the slits, and at an angle θ from the line joining them, so that θ equals the angle of refraction of the beam. Consider two approximately parallel rays from the slits received by the detector.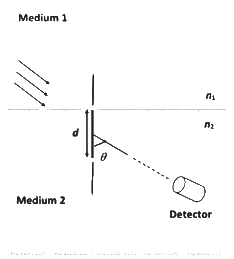
Which of the following statement(s) is(are) correct?
(a) The phase difference between the two rays is independent of d.
(b) The two rays interfere constructively at the detector.
(c) The phase difference between the two rays depends on n1 but is independent of n2.
(d) The phase difference between the two rays vanishes only for certain values of d and the angle of incidence of the beam, with θ being the corresponding angle of refraction. [JEE Advanced 2022 Paper 2]
Ans: (a) & (b)
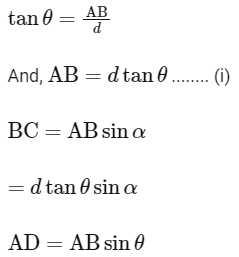
Path difference in vacuum
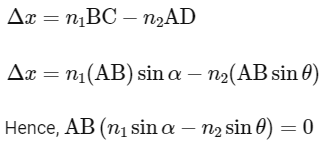
2020
Q1: A parallel beam of light strikes a piece of transparent glass having cross section as shown in the figure below. Correct shape of the emergent wavefront will be (figures are schematic and not drawn to scale)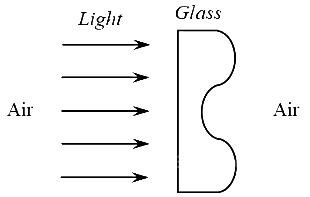 (a)
(a) 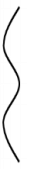
(b) 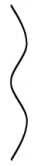
(c) 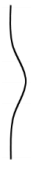
(d) 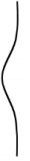
Ans: (a)
Clearly middle part of glass is diverging and upper and lower part are conversing so correct shape of the emergent wavefront is as shown in the figure.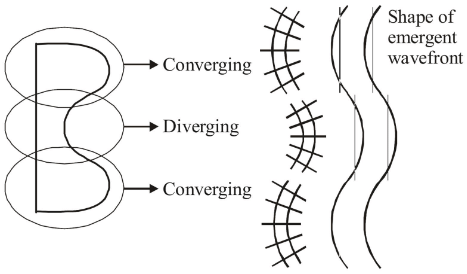
2019
Q1: In a Young's double slit experiment, the slit separation d is 0.3 mm and the screen distance D is 1 m. A parallel beam of light of wavelength 600 nm is incident on the slits at angle α as shown in figure.

Ans: (b)
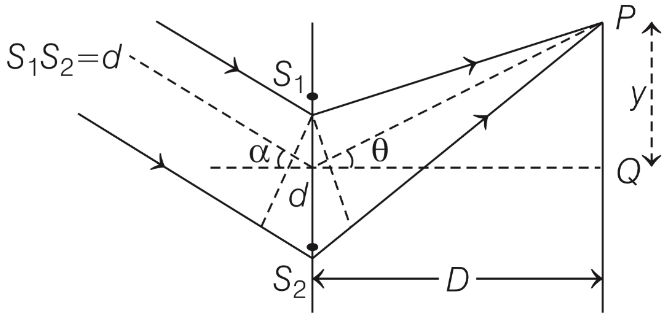
Δx = d sinα + d sinθ
θ and α are small angles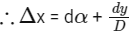
(a) α = 0
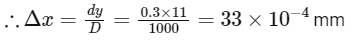
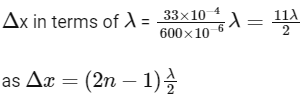
There will be destructive interference.

n =7
So, there will be destruction interference.
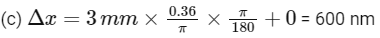
600 nm = nλ ⇒ n = 1
So, there will be construction interference.
(d) Fringe width does not depend on α.
|
297 videos|952 docs|172 tests
|
FAQs on JEE Advanced Previous Year Questions (2018 - 2024): Wave Optics - Physics for JEE Main & Advanced
| 1. What are the key concepts in Wave Optics that are frequently tested in JEE Advanced exams? |  |
| 2. How does Young's Double Slit Experiment demonstrate the principle of interference? |  |
| 3. What is the difference between constructive and destructive interference in Wave Optics? |  |
| 4. How does diffraction depend on the size of the obstacle or aperture relative to the wavelength of light? |  |
| 5. What role does polarization play in Wave Optics, and how can it be achieved? |  |





















