Revision Notes: Alternating Currents | Physics for JEE Main & Advanced PDF Download
Introduction to Alternating Current
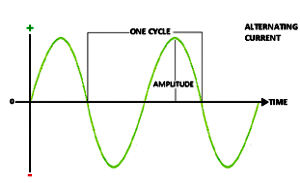
An alternating current (a.c.) is a current which continuously, changes in magnitude and periodically reverses in direction.`
i = I0 sin ωt = I0 sin (2π/T) t
Here I0 is the peak value of a.c.
Basic Parameters and Equations
(a) Current, I =I0 sin ωt(b) Angular frequency, ω= 2πn (n is the frequency of a.c.)
(c) I =I0 sin 2πnt
Mean Value of AC or DC Value of AC
Mean value and its calculation for half-cycle
Mean value of a.c. is that value of steady current which sends the same amount of charge, through a circuit, in same time as is done by a.c. in one half-cycle.
(Iav)half cycle = (2/π)I0
Thus, mean value of alternating current is 2/π times (0.637 times) its peak value.
(Vav)half cycle = (2/π) V0
Average value of AC over a complete cycle
Iav = 0
The average value of a.c. taken over the complete cycle of a.c.is zero.
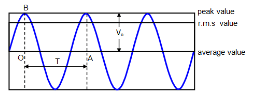
Root Mean Square (RMS) value of AC and its calculation
Root mean square value of alternating current is defined as that value of steady current which produces same heating effect, in a resistance, in a certain time as is produced by the alternating current in same resistance in same time. The r.m.s value of a.c.is also called its virtual value.
Irms = I0/√2
Root mean square value of alternating current is I/√2 times (or 0.707 times) the peak value of current.
Similarly, Vrms= V0/√2
Here V0 is the peak value of e.m.f.
Form Factor
Form Factor = rms value/average value = (V0/√2)/ (2 V0/π) = π/2√2
Current Elements
(a) Inductive reactanceXL = ωL
Here, ω = 2πn, n being frequency of a.c.
L is the coefficient of self-inductance of coil.
(b) Capacitative reactance
Xc = 1/ωC
Here C is the capacity of the condenser
AC Circuits with Components
Capacitor in AC circuit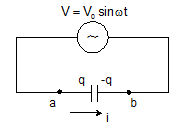
q = CV0sinωt
I = I0 sin(ωt +π/2)
V0 = I0/ωC
Xc = 1/ωC
Inductor in AC circuit
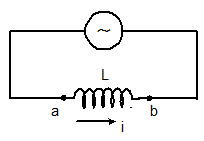
VL = L(dI/dt) = LI0ω cosωt
I = (V0/ ωL) sinωt
Here, I0 = V0/ ωL
XL = ωL
And the maximum current, I0 = V0/XL
R-L circuit
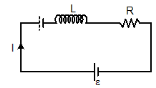
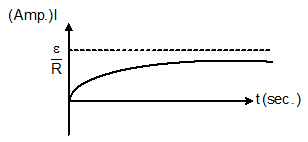
I = ε/R [1-e-Rt/L]
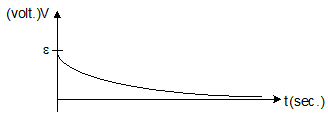
V = ε e-Rt/L
Graph between I (amp) and t (sec):-
Graph between potential difference across inductor and time:-
L-C Circuit:-
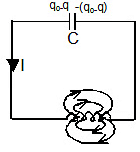
f = 1/2π√LC
q = q0 sin (ωt+ϕ)
I = q0ωsin (ωt+ϕ)
ω = 1/√LC
The total energy of the system remains conserved,
½ CV2 + ½ Li2 = constant = ½ CV02 = ½ Li02
Series in C-R circuit:-
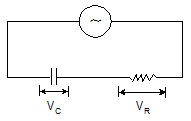
V = IZ
The modulus of impedance, |Z |= √R2+(1/ωC)2
The potential difference lags the current by an angle, ϕ = tan-1(1/ωCR)
Series in L-C-R Circuit:
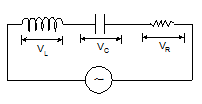
V = IZ
The modulus of impedance, |Z |= √[R2+(ωL-1/ωC)2]
The potential difference lags the current by an angle, ϕ = tan-1[ωL -1/ωC)/R]
Circuit elements with A.C

Resonance and Related Concepts
(a) Resonance frequency:- fr = 1/2π√LC
(b) At resonance, XL = XC, ϕ = 0, Z = R(minimum), cosϕ = 1, sinϕ = 0 nad current is maximum (=E0/R)
Half power frequencies:-
(a) Lower, f1 = fr – R/4πL or ω1 = ωr – R/2L
(b) Upper, f2 = fr + R/4πL or ω2 = ωr + R/2L
Band width:- Δf = R/2πL or Δf = R/L
Quality Factor
(a) Q = ωr/Δω = ωrL/R
(b) As ω = 1/√LC, So Q ∝ √L, Q ∝1/R and Q ∝ 1/√C
(c) Q = 1/ωrCR
(d) Q = XL/R or Q = XC/R
(e) Q = fr/Δf
At resonance, peak voltages are:-
(a) (VL)res = e0Q
(b) (VC)res = e0Q
(c) (VR)res = e0
Conductance, Susceptance, and Admittance
(a) Conductance, G = 1/R
(b) Susceptance, S = 1/X
(c) SL = 1/XL and SC = 1/XC = ωC
(d) Admittance, Y = 1/Z
(e) Impedance add in series while add in parallel
Power in AC Circuits
Circuit containing pure resistance:- Pav = (E0/√2)×(I0/√2) = Ev×IvHere Ev and Iv are the virtual values of e.m.f and the current respectively.
Circuit containing impedance (a combination of R,L and C):-
Pav = (E0/√2)×(I0/√2) cosϕ = (Ev×Iv) cosϕ
Here cosϕ is the power factor.
(a) Circuit containing pure resistance, Pav = EvIv
(b) Circuit containing pure inductance, Pav = 0
(c) Circuit containing pure capacitance, Pav = 0
(d) Circuit containing resistance and inductance,
Z = √R2+(ωL)
cosϕ = R/Z = R/[√{R2+(ωL)2}]
(e) Circuit containing resistance and capacitance:-
Z = √R2+(1/ωC)2
cosϕ = R/Z = R/[√{R2+(1/ωC)2}]
(f) Power factor, cosϕ = Real power/Virtual power = Pav/ErmsIrms
Transformer
(a) Cp = Np (dϕ/dt) and es = Ns (dϕ/dt)
(b) ep/es = Np/Ns
(c) As, epIp = esIs, Thus, Is/Ip = ep/es = Np/Ns
(d) Step down:- es < ep, Ns< Np and Is> Ip
(e) Step up:- es >ep, Ns>Np and Is< Ip
(f) Efficiency, η = es Is/ ep Ip
AC Generator
e = e0 sin (2πft)
Here, e0 = NBAω
|
268 videos|732 docs|171 tests
|
















