Important Formulas: Simplification | General Test Preparation for CUET UG - CUET Commerce PDF Download

BODMAS Rule

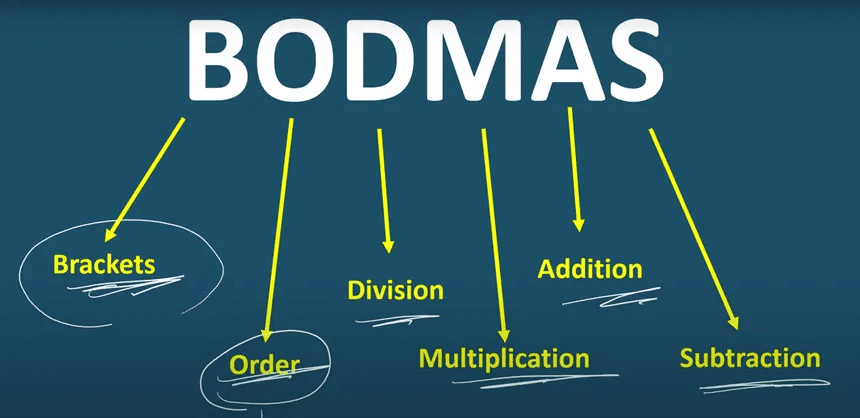
The BODMAS rule dictates the order in which operations should be performed to evaluate an expression correctly. The acronym stands for:

B - Brackets (First, solve anything inside brackets: (), {}, [])

O - Of (This represents powers or exponents, e.g., 2²)

D - Division (Next, perform division)

M - Multiplication (Next, perform multiplication)

A - Addition (After multiplication/division, perform addition)

S - Subtraction (Finally, perform subtraction)

In simplification, start by solving expressions inside brackets, then move on to exponents, followed by division, multiplication, addition, and subtraction in the order listed.

Modulus of a Real Number

The modulus (or absolute value) of a real number a is defined as:

|a| = a if a > 0

|a| = -a if a < 0

For example:

|5| = 5

|-5| = 5 (since -(-5) = 5).

Vernacular (or Bar)

When an expression involves a Vernacular (often represented as a bar), simplify the expression under the Vernacular first before applying the BODMAS rule.

Roots

Roots, or radicals, are the opposite of exponents. For example, the square root of 4 is 2, as 2² = 4. The square root of 9 is 3, since 3² = 9.

• The square root is written as √.
• Cube roots are written as ∛.
• Similarly, the fourth root is ∜, and so on.

For example:

√9 = 3

∛27 = 3 (cube root of 27).

Simplifying Square Root Terms

To simplify a square root expression:

1. Extract perfect squares. For example, √4 = 2, √9 = 3.
2. If the argument inside the square root isn't a perfect square but can be factored, break it down into factors, and then simplify the expression.

For example:

• √18 = √(9 * 2) = √9 * √2 = 3√2.

Important Formulas for Simplification

Here is a list of important formulas that can be helpful when simplifying expressions:

1. BODMAS Rule (Order of Operations)

• Brackets: Solve operations inside brackets first ( (), {}, [])
• Orders: Apply exponents (powers) like squares, cubes, etc.
• Division and Multiplication: Solve division and multiplication from left to right.
• Addition and Subtraction: Solve addition and subtraction from left to right.

2. Percentage Calculations

• Percentage Formula:
  Percentage = (Part / Whole) * 100
  To find the percentage of a number:
  Percentage of a number = (P / 100) * X
  Where P is the percentage and X is the number.

• Finding a Number from Percentage:
  X = (Percentage * Whole) / 100

3. Average Formula

• Average:
  Average = (Sum of all values) / (Number of values)

4. Simplifying Fractions

• Simplifying a Fraction:
  Simplified Fraction = (Numerator / Denominator) (divide both by the greatest common divisor)

• Multiplying Fractions:
  (a / b) * (c / d) = (a * c) / (b * d)

• Dividing Fractions:
  (a / b) ÷ (c / d) = (a / b) * (d / c) = (a * d) / (b * c)

5. Simplification of Square Roots

• Square Root of a Product:
  √(a * b) = √a * √b

• Square Root of a Quotient:
  √(a / b) = √a / √b

• Square of a Number:
  (a)² = a * a

6. Simplification of Cube Roots

• Cube Root of a Product:
  ∛(a * b) = ∛a * ∛b

• Cube Root of a Quotient:
  ∛(a / b) = ∛a / ∛b

7. Exponent Rules

• Multiplying Powers with Same Base:
  a^m * aⁿ = a^{(m + n)}

• Dividing Powers with Same Base:
  a^m / aⁿ = a^{(m + n)}

• Power of a Power:
  (a^m)ⁿ = a^{(m * n)}

• Multiplying Powers with Different Bases but Same Exponent:
  aⁿ * bⁿ = (a * b)ⁿ

• Negative Exponent Rule:
  a^(-n) = 1 / aⁿ

8. Surds and Radicals

• Simplifying Square Roots:
  To simplify square roots, look for perfect squares inside the root.
  Example: √18 = √(9 * 2) = √9 * √2 = 3√2

• Simplifying Cube Roots:
  Similar to square roots, simplify cube roots by factoring out perfect cubes.
  Example: ∛54 = ∛(27 * 2) = ∛27 * ∛2 = 3∛2

9. Logarithms (for advanced simplification)

• Logarithmic Properties:
  log_b(x * y) = log_b x + log_b y
  log_b(x / y) = log_b x - log_b y
  log_b(x^n) = n * log_b x
  log_b b = 1 and log_b 1 = 0

10. Percentage Increase and Decrease

• Percentage Increase:
  New Value = Original Value * (1 + (P / 100))

• Percentage Decrease:
  New Value = Original Value * (1 - (P / 100))

11. Solving Simple Equations

• Linear Equations:
  For equations like ax + b = 0, solve for x:
  x = -b / a

• Quadratic Equations:
  For equations of the form ax² + bx + c = 0, use the quadratic formula:
  x = (-b ± √(b² - 4ac)) / (2a)

Solved Examples for Simplification

Example 1: The price of 10 chairs is equal to that of 4 tables. The price of 15 chairs and 2 tables together is Rs. 4000. Find the total price of 12 chairs and 3 tables.

Solution: Let the cost of a chair be Rs. x and the cost of a table be Rs. y.

From the given, we know: Price of 10 chairs = Price of 4 tables → 10x = 4y This simplifies to: y = (5/2)x

We are also told that the price of 15 chairs and 2 tables is Rs. 4000: 15x + 2y = 4000

Substitute y = (5/2)x into this equation: 15x + 2 * (5/2)x = 4000 15x + 5x = 4000 20x = 4000 → x = 200

Now substitute x = 200 into y = (5/2)x: y = (5/2) * 200 = 500

The total price of 12 chairs and 3 tables is: 12x + 3y = 12 * 200 + 3 * 500 = 2400 + 1500 = 3900

Thus, the total cost is Rs. 3900.