Quant Practice Questions for ACT - 4 | Mathematics for ACT PDF Download
Q1: O is the center. Find x
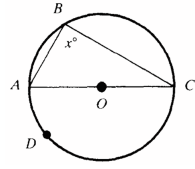
 View Answer
View AnswerAns: AC is a diameter and ADC is a semi-circle whose measure is 180°.
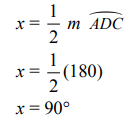
Note: Any angle inscribed in a semi-circle is aright angle.
Q2: O is the center. Find x.
 View Answer
View AnswerAns: BC is a diameter (a chord that passes through the center of the circle forming 2 equal arcs of 180 ° each). Angle B is an inscribed angle. The measure of AC is 60° and the measure of BAC is180°. Therefore:

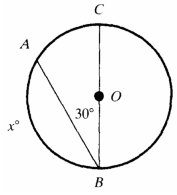
Q3: If the three arcs of the circle measure x°, x°, and (3x + 10)°, find inscribed ∠y.
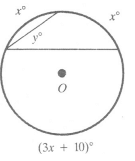
 View Answer
View AnswerAns: Find x by using the equation:
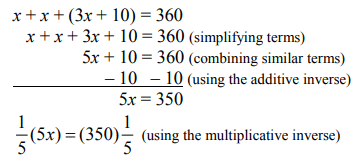
x = 70°
Since y is the measure of an inscribed angle, it measures 1/2 (x) = 35°
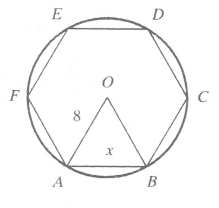
Q4: O is the center; ABCDEF is a regular hexagon inscribed in the circle whose sides are eight units long. Find x.
 View Answer
View AnswerAns: A regular hexagon is a polygon whose six sides and six angles are congruent. Its central angle measures 60° (360 ÷ 6 = 60°). Triangle AOB is isosceles and ∠OAB = ∠OBA. A regular hexagon contains 6 equilateral triangles. Thus x = 8. An inscribed angle is an angle whose vertex is on the circle and whose sides are chords of the circle. A chord is a line drawn within a circle touching two points on the circumference of the circle.
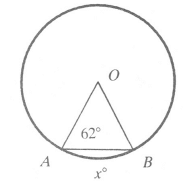
Q5: O is the center. The measure of ∠A is 62°. Find x.
 View Answer
View AnswerAns: To find x, find the number of degrees in the central ∠AOB. OA and OB are radii in the same circle and are, therefore, equal. The angles opposite these equal sides are equal, so m ∠B = 62°
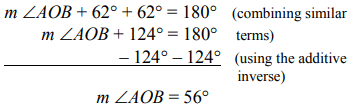
Since central ∠AOB measures 56°, its intercepted arc measures 56°
Q6: What is the measure of the obtuse angle formed by the two hands of a clock at 5 P.M.?
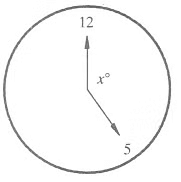
 View Answer
View AnswerAns:
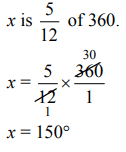
Q7: Find the circumference of a circle if the length of its radius is 5”. (Use π = 3.14).
 View Answer
View AnswerAns: Since radius = 5, diameter = 10
C = πd
C = (3.14)(10)
C = 31.4”
Q8: Approximate the circumference of a circle with a radius of 21 inches. Use 22/7 as an approximation for π.
 View Answer
View AnswerAns:
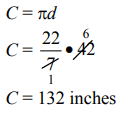
Q9: In the figure, ABC is a 45°-45°-90° triangle with AC = 6. Find AB and BC.
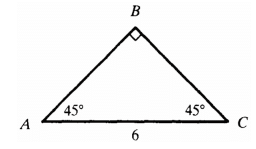
 View Answer
View AnswerAns:
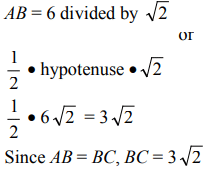
Q10: ∆DEF is a 30°-60°-90° triangle, and EF = 4. Find the measure of DF and DE .
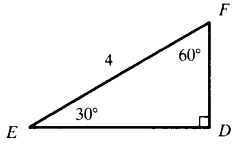
 View Answer
View AnswerAns: DF is the side opposite the 30° angle, so its measure is one-half the hypotenuse. Since EF = 4, DF = 2. DE is the side opposite the 60° angle, so its measure is one-half the hypotenuse times √3 .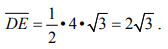
|
144 videos|100 docs|61 tests
|
FAQs on Quant Practice Questions for ACT - 4 - Mathematics for ACT
| 1. How can I improve my ACT Math score? |  |
| 2. What topics are covered in the ACT Math section? |  |
| 3. Is a calculator allowed on the ACT Math section? |  |
| 4. How should I manage my time when taking the ACT Math section? |  |
| 5. Are there any strategies I can use to approach ACT Math questions more effectively? |  |




















