Conductors, Capacitors & Dielectrics | Electricity & Magnetism - Physics PDF Download
| Table of contents |

|
| Basic Properties of Conductors |

|
| Capacitors |

|
| Capacitance of a Parallel Plate Capacitor |

|
| Dielectrics |

|
| How Does a Dielectric Increases Capacitance? |

|
Basic Properties of Conductors
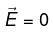 inside a conductor.
inside a conductor.- ρ = 0 inside a conductor.
- Any net charge resides on the surface.
- A conductor is an equipotential.
 is perpendicular to the surface, just outside a conductor.
is perpendicular to the surface, just outside a conductor.
Because the field inside a conductor is zero, the boundary condition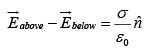 requires that the field immediately outside is
requires that the field immediately outside is 
In terms of the potential equation,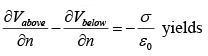

These equations enable us to calculate the surface charge on a conductor if we can determine  or V.
or V.
The force per unit area on the conductor is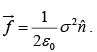
This amounts to an outwards electrostatic pressure on the surface, tending to draw the conductor into the field, regardless of the sign of σ. Expressing the pressure in terms of the field just outside the surface, 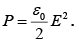
Example 5: A spherical conductor of radius a is placed in a uniform electric field 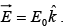 The potential at a point P (r,θ) for r >a, is given by
The potential at a point P (r,θ) for r >a, is given by 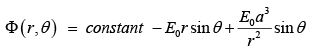 where r is the distance of P from the center O of the sphere and θ is the angle OP makes with the z-axis. Then the charge density on the sphere at θ = 60° is
where r is the distance of P from the center O of the sphere and θ is the angle OP makes with the z-axis. Then the charge density on the sphere at θ = 60° is 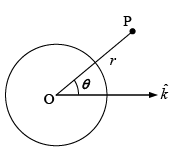
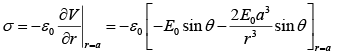
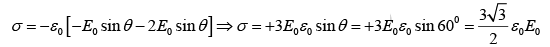
Example 6: Two spherical cavities, of radii a and b, are hollowed out from the interior of a conducting sphere of radius R . At the center of each cavity a point charge is placed, call these charges qa and qb.
(a) Find the surface charges σa, σb andσR.
(b) What is the field outside the conductor?
(c) What is the field within each cavity?
(d) What is the force on qa and qb?
(e) If a third charge qc, were brought near the conductor, which of the above answers would change? 
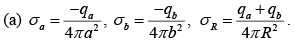

(d) Zero
(e) σR will change and hence the electric field outside the conductor will also change.
Capacitors
- A capacitor is a device utilized for storing electric charge, with applications ranging from filtering static in radio reception to storing energy in heart defibrillators. Typically, commercial capacitors consist of two conducting parts placed close together but not touching.
- An insulator is often used between the two plates to provide separation, as discussed further below in the section on dielectrics.
- When battery terminals are connected to an initially uncharged capacitor, equal amounts of a positive and negative charge, +Q and –Q, are separated into two plates. While the capacitor remains neutral overall, we describe it as storing a charge Q in this scenario.
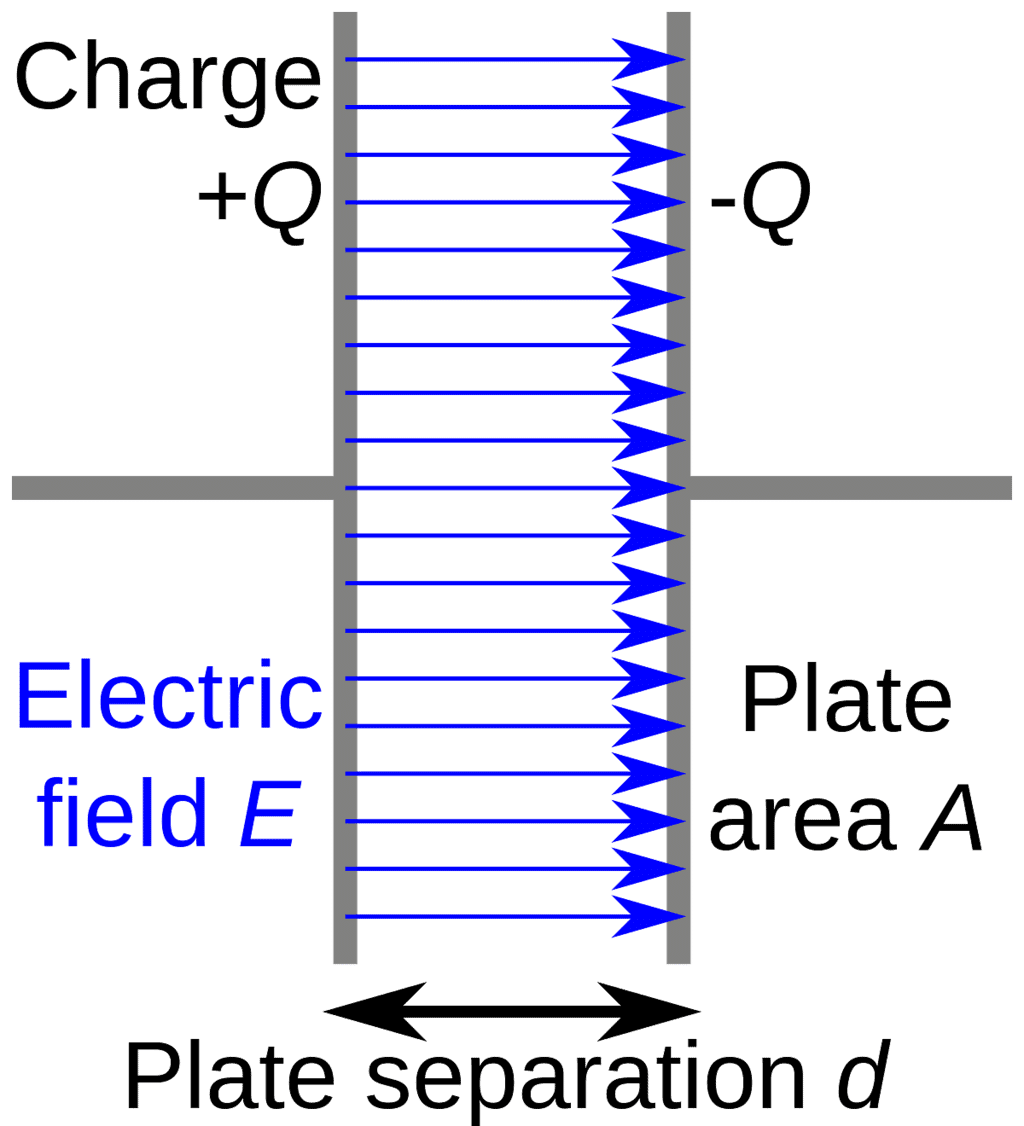 Parallel plate capacitor
Parallel plate capacitor
- The amount of charge Q a capacitor can store depends on two major factors—the voltage applied and the capacitor’s physical characteristics, such as its size.
- A system consisting of two identical, parallel conducting plates separated by a distance, as depicted in the diagram above, is termed a parallel plate capacitor.
- Each electric field line originates from an individual positive charge and terminates at a negative charge, indicating that more field lines correspond to a greater amount of charge. Consequently, the electric field strength is directly proportional to Q.
E ∝ Q
we know that the voltage across parallel plates is
V = Ed.
Thus, V∝E. It follows, then, that V∝Q, and conversely,
Q∝V
- The amount of charge stored in a capacitor increases with the applied voltage.
- Capacitors with different physical characteristics will store varying amounts of charge for the same applied voltage. We define capacitance, denoted as C, such that the charge Q stored in a capacitor is directly proportional to C. The charge stored in a capacitor can be calculated using the equation Q = CV, where Q is the charge, C is the capacitance, and V is the voltage.
- This equation highlights the two main factors influencing the charge stored: the physical characteristics of the capacitor (C) and the voltage (V). Rearranging the equation, we find that capacitance (C) is the amount of charge stored per volt, expressed as
C = Q/V
- The unit of capacitance is the farad (F), named for Michael Faraday (1791–1867), an English scientist who contributed to the fields of electromagnetism and electrochemistry. Since capacitance is the charge per unit voltage, we see that a farad is a coulomb per volt.
Capacitance of a Parallel Plate Capacitor
- It can be shown that for a parallel plate capacitor, there are only two factors (A and d) that affect its capacitance C. The capacitance of a parallel plate capacitor in equation form is given by:
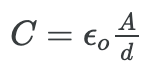
The constant ε0 is the permittivity of free space; its numerical value in SI units is ε0 = 8.85 × 10−12 F/m.
Example 1: What is the capacitance of a parallel plate capacitor with metal plates, each of area 1.00 m2, separated by 1.00 mm?Solution: To calculate the capacitance of a parallel plate capacitor, we can use the formula:
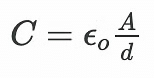
where: C is the capacitance, εo is the vacuum permittivity (8.85×10-12 F/m), A is the area of each plate (1.00 m²), d is the separation between the plates (1.00 mm = 0.001 m). Plugging in the values, we get:
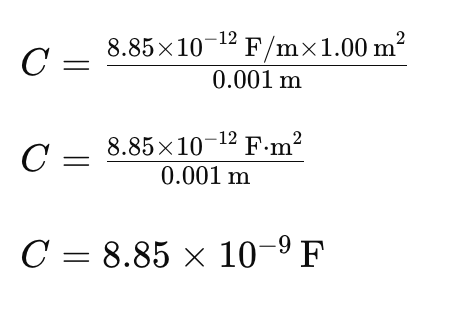 Dielectrics
Dielectrics
- It is clear from the mathematical expression of the capacitance of a parallel plate capacitor that to increase the charge-storing capacity of a capacitor, we need to reduce the value of d. But this is not a viable practical solution to reduce the value of d. This can cause a breakdown as the value of voltage will also increase (E=V/d).
- To address this challenge, a key approach is to insert an insulating material, known as a dielectric, between the plates of a capacitor and minimize the distance, d, between them. Reducing d not only increases the capacitance but also allows many insulators to endure higher electric fields than air without breaking down.
- For a parallel plate capacitor, with a dielectric, the value of capacitance is given as:
 where k is the dielectric constant.
where k is the dielectric constant. - Values of the dielectric constant κ for various materials are given in the table below. Note that κ for vacuum is exactly 1, and so the above equation is valid in that case, too.
 Dielectric Constants of various materials
Dielectric Constants of various materials
- The dielectric constant for air is very close to 1 so air-filled capacitors act much like those with a vacuum between their plates.
- The maximum electric field strength above which an insulating material begins to break down and conduct is called its dielectric strength.
How Does a Dielectric Increases Capacitance?
The increase in capacitance of a capacitor with dielectric can be explained in two ways:
- On a microscopic level, the increase in capacitance due to a dielectric is attributed to the polarization of the insulator. The ease of polarization is determined by the insulator's dielectric constant, κ.
- For instance, water is polar because one end of its molecule carries a slight positive charge while the other end bears a slight negative charge. This polarity grants water a relatively high dielectric constant of 80. The concept of polarization is best understood through the characteristics of the Coulomb force.
- The Coulomb force between the nearest ends of the molecules and the charges on the plates is attractive and robust because of their proximity. This attraction leads to a greater accumulation of charge on the plates compared to a space with opposite charges at a distance d away.
 Polarisation caused due to the presence of dielectric
Polarisation caused due to the presence of dielectric
- Another approach to understanding how a dielectric enhances capacitance is to examine its impact on the electric field inside the capacitor.
- As these lines terminate on charges within the dielectric, fewer lines traverse from one side of the capacitor to the other.
- Consequently, the electric field strength is diminished compared to a vacuum between the plates, despite the same charge existing on the plate due to the presence of the dielectric.
- Consequently, for the same charge Q, there is a lower voltage V, and since C= Q/V, the capacitance C is increased.
 Electric field inside the capacitor with dielectric
Electric field inside the capacitor with dielectric
Example 2: Find the capacitance of a parallel plate capacitor having plates of area 5.00 m2 that are separated by 0.100 mm of Teflon.
Solution: To find the capacitance of the parallel plate capacitor with a dielectric, we can use the formula:
where C is the capacitance
ε is the permittivity of Teflon, which is, 2.1×10-11 F/m
A is the area, which is, 5.00 m2
d is the separation between the plates, which is, 0.1 mm=0.0001 m
Plugging the values, we get
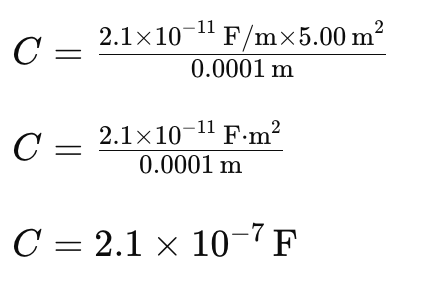
Example 3: A certain parallel plate capacitor has plates of area 4.00 m2, separated by 0.0100 mm of nylon, and stores 0.170 C of charge. What is the applied voltage?
Solution: To find the capacitance of the parallel plate capacitor with a dielectric, we can use the formula:
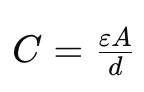
where C is the capacitance
ε is the permittivity of Nylon, which is, 3.0×10-11 F/m
A is the area, which is, 4.00 m2
d is the separation between the plates, which is, 0.01 mm=0.00001 m
Plugging the values, we get
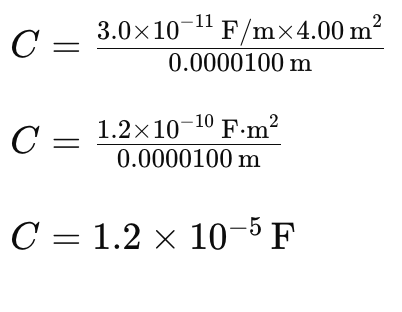 Now we know that, C=Q/V
Now we know that, C=Q/V
where, Q= 0.170 C
V=Q/C
V=(0.170)/(1.2 x 10-5)
V=14,166.67 V
|
82 videos|32 docs|22 tests
|
FAQs on Conductors, Capacitors & Dielectrics - Electricity & Magnetism - Physics
| 1. How does the capacitance of a parallel plate capacitor depend on the area of the plates and the distance between them? |  |
| 2. What role does the dielectric material play in increasing the capacitance of a capacitor? |  |
| 3. How does the presence of a conductor affect the capacitance of a capacitor? |  |
| 4. Can the capacitance of a capacitor be negative? |  |
| 5. How does the dielectric strength of a material affect the capacitance of a capacitor? |  |




















