Overview: Ratio and Proportion | CSAT Preparation - UPSC PDF Download
| Table of contents |

|
| Importance in CSAT |

|
| Ratio |

|
| Classification of Ratio |

|
| Proportion |

|
| Solved Questions |

|
Importance in CSAT
Basics of the ratio and proportion are very important for CSAT exams. Questions are not asked directly but the concepts that are used in this chapter play an important role in the CSAT exam. It also works as a base for Data Interpretation too. The topic from which questions are generally asked are as follows
- Ratio of milk and water.
- Ratio of salary and expenditure.
- Mixtures
- Partnership
In the year 2023 and 2022 two question was asked but in the years 2021-2018 atleast 1 question was asked from this chapter.
Ratio
A ratio compares two or more quantities of the same type by dividing them. It shows how one quantity relates to another in terms of size. In simpler terms, the ratio of two quantities tells us how many times one quantity fits into the other.
If we have two quantities, a and b, then the ratio of a to b is written as a/b. This means the ratio of two quantities is the same as the fraction of one quantity compared to the other.
So, when we say the ratio of a to b, we write it as a a:b
The first term of the ratio is called the antecedent, and the second term is called the consequent.
For example, the ratio between 30 kg and 50 kg is written as 3:5.
A ratio stays the same if each term of the ratio is multiplied or divided by the same number.
For instance, the ratio 4:3 remains unchanged if both terms are multiplied or divided by 10, resulting in 40:30.
Illustration : The total number of students in a class is 95. If the total number of girls in the class is 45, then the ratio of the total number of boys to the total number of girls is:
(a) 9 : 10
(b) 7 : 8
(c) 10 : 9
(d) 9 : 11
Solution: (c)
Let the total number of boys in the class be x.
According to the question:
x + 45 = 95
x = 95-45 =50
Hence, the required ratio of the total number of boys to the total number of girls is: B: G= 50:45=10:9
Classification of Ratio
Ratios are classified as given below1. Duplicate Ratio: The duplicate ratio of a:b is a2 b2
Example: Duplicate ratio of 6:11 is 36: 121
2. Triplicate Ratio: a3:b3 is called triplicate ratio of a:b
Example: Triplicate Ratio of 3:5 is 27: 125
3. Subduplicate Ratio: The subduplicate ratio of a:b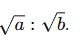
Example: Sub duplicate ratio of 25: 36 is 5: 6
4. Subtriplicate Ratio: 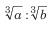 is called subtriplicate ratio of a:b
is called subtriplicate ratio of a:b
Example: Subtriplicate ratio of 216: 343 is 6:7
5. Compound Ratio: ab: cd is the compound ratio of a: c and b: d. It is the ratio of the product of the antecedents to that of the consequents of two or more given ratios.
6. Inverse Ratio: 1/a: 1/b is the inverse ratio of a:b.
Example: Inverse Ratio of 3: 4 is 1/3 : 1/4 or 4: 3
Ratio can only be formed between quantities that have the same unit. For example, you can compare Rs.64 and Rs.96 because they are both numbers. However, you cannot establish a ratio between 64 (a number) and 96 kg (a weight) because they are different types of quantities.
Illustration: If 378 coins consist of ₹1, 50 paise, and 25 paise whose values are proportional to 13 : 11 : 7, then the number of 50 paise coins will be:
(a) 136
(b) 133
(c) 132
(d) 128
Solution: (c)
Let the values of ₹1, 50 paise, and 25 paise coins be 13x, 11x, and 7x, respectively.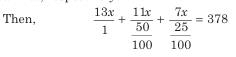
Since paise is to be converted into rupees by dividing by 100, so 50 paise and 25 paise are divided by 100.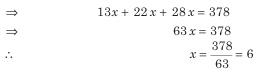
So the Number of coins = 22x6 is 132
Relation among More than Two Quantities
1. For three quantities: If A:B = x1: y1 an d 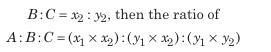
2. For Four Quantities: If A: B= N1: D1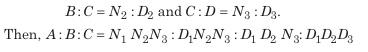
Illustration: The sum of squares of three numbers is 532 and the ratio of the first to the second and also ratio of the second to the third is 3:2. What is the second number?
(a) 2
(b) 6
(c) 12
(d) None of these
Solution: (c) Let the three numbers be a,b and c respectively
Then a:b= 3:2
b:c =3:2
a:b:c = 3 x 3 : 2 x 3: 2 x 2 = 9:6:4
So, a=9x, b=6x , c=4x (here, x is the common ratio)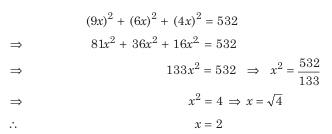
Dividing a Given Number in the Given Ratio
(a) If the two numbers are in the ratio a1:a2 and the sum of these number is A, then these numbers will be
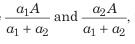 respectively.
respectively.
If a mixture of A L, two liquids P and Q are in the ratio of a1: a2, then the quantities of liquids P and Q in the mixture will be
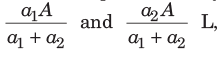 respectively.
respectively.
If three numbers are in the ratio of a1: a2: a3 and the sum of these numbers is A, then these numbers will be 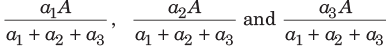 respectively.
respectively.
Illustration. If ratio of two numbers is 20 : 39 and there sum is 295, then these numbers are
(a) 100, 195
(b) 150, 145
(c) 105, 190
(d) 110, 185
Sol. (a)
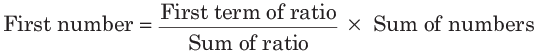
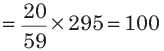
Second number
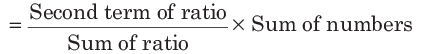
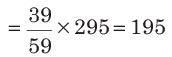
So, the two numbers are 100 and 195.
Elementary Formulae on Ratios
FORMULA 1
If the ratio of two numbers is a : b, then the number that should be subtracted from each of the numbers in order to make this ratio c : d is given by 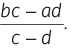
Illustration. If the ratio between two numbers is 8 : 17, then what number should be subtracted to make this ratio 2 : 5 ?
(a) 2
(b) 4
(c) 5
(d) 3
Sol. (a) According to the formula,
Subtracted number = 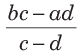
Here, a = 8, b = 17, c = 2 and d = 5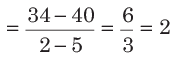
FORMULA 2
If the ratio of incomes of two persons is a : b and their expenditures in the ratio of c : d and if each saves Rs. x, then their incomes are 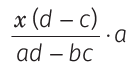 and
and 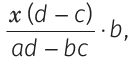 respectively and their expenditures are
respectively and their expenditures are 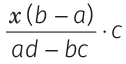 and
and 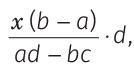 respectively.
respectively.
Illustration. The ratio of incomes of Rohit and Pratap is 4 : 3 and ratio of their expenditures is 3 : 2, if each saves Rs. 2500, then their incomes are
(a) Rs. 12000, Rs. 9000
(b) Rs. 8000, Rs. 6000
(c) Rs. 10000, Rs. 7500
(d) None of these
Sol. (c) Let the incomes of Rohit and Pratap be Rs. 4 x and Rs. 3 x respectively, also their expenditures are Rs. 3 y and Rs. 2 y, respectively.
Then, according to the question,
4x − 3 y = 2500 …(i)
and 3x − 2 y = 2500 …(ii)
On solving Eqs. (i) and (ii),
we get x = 2500
and y = 2500
∴ Income of Rohit = 4 × x = 4 × 2500 = Rs. 10000
and income of Pratap = 3 × x = 3 × 2500 = Rs. 7500
Proportion
The equality of two ratios is called proportion. a , b, c and d are said to be in proportion, if a : b = c : d or a : b :: c : d. Here, a is the first term, b is the second term, c is the third term and d is the fourth term. Here, first and fourth terms are called extremes i.e. a and d, while the second and third terms are called as means i.e. b and c. e.g. If 3 : 2 : : 135 : 90, then 3 and 90 are called the extremes, while 2 and 135 are called the means.
In a proportion, we always have
Product of extremes = Product of means
a:b::c:d
⇒ a × d = b× c
Illustration. Find a fraction which bears same ratio to 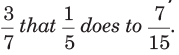
(a) 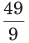
(b)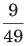
(c)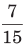
(d)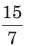
Sol. (b) Let the fraction be x.
Then, according to the formula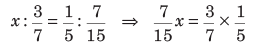
⇒ 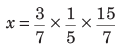
∴ 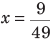
Classification of Proportion Proportion is divided into three types:
1. Continued proportion If three quantities a, b and c are such that a : b : : b : c, then b ac 2 = and a , b and c are in continued proportion. Also, the quantity c is called the third proportion of a and b.
2. Mean proportion If three quantities a , b and x are such that a : x : : x : b, then x ab 2 = and x is called the mean proportion of a and b.
∴ x = √ab
3. Fourth proportion If four quantities a , b, c and x are such that a : b : : c : x, then ax = bc and x is called the fourth proportion of a , b and c.
- Invertendo If a : b : : c : d , then b : a : : d : c
- Alternendo If a : b : : c : d , then a : c = b : d
- Componendo If a : b : : c : d , then (a + b) : b : : (c + d ) : d
- Dividendo If a : b : : c : d , then (a − b) : b : :(c − d ) : d
- Componendo-dividendo If a : b : : c : d, then
(a + b) : (a − b) : : (c + d ) : (c − d )
Illustration. If 4,6 and x are in continued proportion, then what is the value of x ?
(a) 14
(b) 16
(c) 9
(d) 12
Sol. (c). When 4, 6 and x are in continued proportion, then these are written as
4 : 6 :: 6 : x
∵ a : b :: b : c
Now, by applying the condition of continued proportion
b2 ac 2 = ⇒ (6)2 = 4 × x
⇒ 36 = 4x
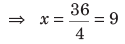
Unitary Method
It is a method in which the value of a quantity is first obtained to find the value of any required quantity.
For solving problems on unitary method two kinds of proportion are used.
1. Direct proportion: Two quantities are said to be directly proportional, if one of them increases or decreases proportionally, then the other increases or decreases to the same extent. e.g.
(i) More the numbers of articles, more is the cost.
(ii) More the number of workers, more is the work done.
(iii) Less the number of articles, less is the cost.
(iv) Less the number of workers, less is the work done.
2. Indirect proportion: Two quantities are said to be indirectly proportional, if one of them increases or decreases proportionally, then the other decreases or increases to the same extent. e.g.
(i) More the number of workers, less is the number of days required to finish a work.
(ii) More the speed, less is the time taken to cover a certain distance.
(iii) Less the number of workers, more is the number of days required to finish a work.
(iv) Less the speed, more is the time taken to cover a certain distance.
Illustration. If cost of 15 eggs be Rs. 75, then find out the cost of 5 dozen eggs.
(a) Rs. 300
(b) Rs. 400
(c) Rs. 500
(d) Rs. 600
Sol. (a) Cost of 15 eggs = Rs. 75
Cost of 1 egg = 
Now, cost of 5 dozen, i.e. 5 × 12 = 60 eggs = 60 × 5 = Rs. 300
Alternate Method
Let the cost of 5 dozen (i.e. 5 × 12 = 60) eggs = Rs. x
Then, using direct proportion,
More eggs, More cost
15 : 75 :: 60 : x
⇒ 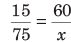
∴ 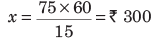
Solved Questions
Q1: In a library, the ratio of the number of story books to that of non-story books was 4:3 and total number of story books was 1248. When some more story books were bought, the ratio became 5:3. Find the number of story books bought.
Ans: Option A
Explanation:

Q2: Rs. 8400 is divided among A, B, C and D in such a way that the shares of A and B, B and C, and C and D are in the ratios of 2:3, 4:5, and 6:7 respectively. The share of A is
Ans: Option A
Explanation:

Q3: The ratio of the present age of father to that of son is 7:2. After 10 years their ages will be in the ratio of 9:4. The present ages of the father is
Ans: Option A
Explanation:

Q4: Ajay and Raj together have Rs. 1050. On taking Rs. 150 from Ajay, Ajay will have same amount as what Raj had earlier. Find the ratio of amounts with Ajay and Raj initially.
Ans: Option D
Explanation:

Q5: Price of each article of type P, Q, and R is Rs. 300, Rs. 180 and Rs. 120 respectively. Suresh buys articles of each type in the ratio 3:2:3 in Rs. 6480. How many articles of type Q did he purchase?
a. 8
Ans: Option A
Explanation:

Q6: Divide Rs. 60 in the ratio 1:2 between Mike and John.
Solution: Let Mike’s part be x.
Then John’s part is 2x.
Thus, x+2x = 60
3x = 60
x = (60/3)
x = 20.
Therefore, Mike’s part = x = Rs. 20
John’s part = 3x = Rs. (2*20) = Rs. 40
Q7: Three Jars contain alcohol to water in the ratios 3:5, 1:3, and 1:1. If all the three solutions are mixed, what will be the ratio of alcohol to water in final solution?
Solution: Here we are not given the quantities of the solution in three jars. Only the ratio of alcohol to water is given. If the ratio of the quantity of solution would have been there, we could determine the ratio of alcohol to water in the final solution. Hence, the answer here will be cannot be determined.
Q8: If there are Rs. 495 in a bag in denominations of one-rupee, 50-paisa, and 25-paisa coins which are in the ratio 1:8:16. How many 50 paisa coins are there in bag?
Solution: Assume, you have x numbers of one rupee coin. Now coins are in the ratio 1:8:16. This means that if we have x number of one rupee coins, we have 8x number of 50 paisa coins and 16x number of 25 paisa coins. Here order in which ratios are mentioned in the question is very important. In this case, order is one rupee, 50 paisa and 25 paisa and ratio is 1:8:16. Thus,
Number of 50-paisa coins = 8x
Number of 25- paisa coins = 16x
Now,Total money in the bag = Rs. 495
- x+ (8x/2) + (16x/4) = 495
(50 paisa coins divided by 2 to convert into rupee and 25 paisa coins divided by 4 to convert into rupee)
- 9x = 495
- x = 495/9
- x= 55
Thus, number of 50 paisa coins = 55*8 = 440
|
205 videos|264 docs|136 tests
|
FAQs on Overview: Ratio and Proportion - CSAT Preparation - UPSC
| 1. What is the difference between a ratio and a proportion? |  |
| 2. How can the unitary method be used to solve ratio and proportion problems? |  |
| 3. Can you provide some simple methods to solve ratio and proportion questions? |  |
| 4. What are some common elementary formulae related to ratios? |  |
| 5. How are ratios classified? |  |
















