House of Hundreds - II Chapter Notes | Mathematics for Class 3 (Maths Mela) PDF Download
Introduction
Welcome to the "House of Hundreds," where we learn about three-digit numbers. In this chapter, we'll learn about counting, make fun number patterns, and solve puzzles together. Get ready to discover the secrets of numbers and become counting champions!
Let's Know the number neighbours
Imagine you have the number 234. We're going to find the numbers that are close to 234, but in terms of hundreds, 50s, and 10s. Let's break it down step-by-step.
Neighbouring Hundreds
Neighbouring hundreds are the closest multiples of 100 around your number. For 234, we look for the nearest hundreds before and after it.
- Lower neighbouring hundred: The closest multiple of 100 before 234 is 200.
- Upper neighbouring hundred: The closest multiple of 100 after 234 is 300.
So, the neighbouring hundreds of 234 are 200 and 300.

Neighbouring 50s
Neighbouring 50s are the closest multiples of 50 around your number. For 234, we look for the nearest 50s before and after it.
- Lower neighboring 50: The closest multiple of 50 before 234 is 200. (Though 200 is also a neighboring hundred, it can also be considered here.)
- Upper neighboring 50: The next multiple of 50 after 234 is 250.
So, the neighbouring 50s of 234 are 200 and 250.

Neighbouring 10s
Neighbouring 10s are the closest multiples of 10 around your number. For 234, we look for the nearest 10s before and after it.
- Lower neighbouring 10: The closest multiple of 10 before 234 is 230.
- Upper neighbouring 10: The closest multiple of 10 after 234 is 240.
So, the neighbouring 10s of 234 are 230 and 240.

Different Ways of Representing Numbers
Let's explore different ways to represent the numbers.
Let's take a number, 456. Here are various ways to write or represent it:
Using "more than" a base number:- 156 more than 300
- 4 hundreds, 5 tens, 6 ones
- 456
- 400 + 50 + 6
- 44 less than 500
- 500 - 44
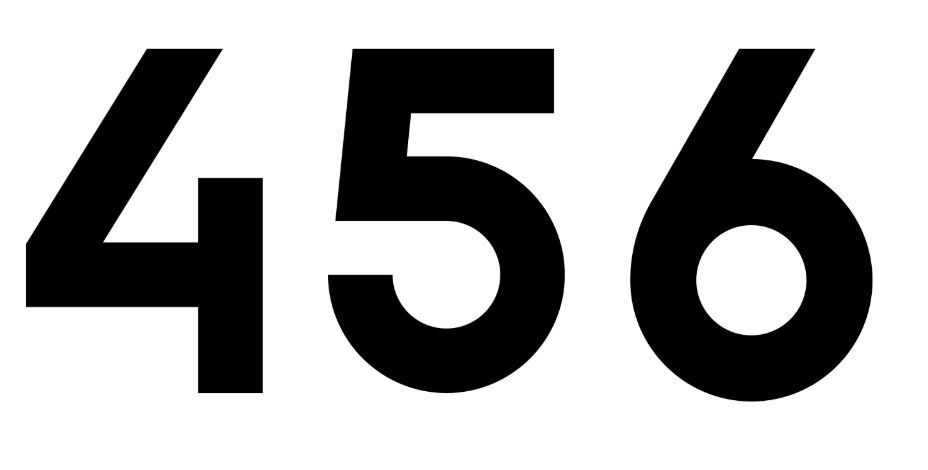
Let's Practice:
68 more than 300:
- 368 (68 + 300)
- Breaking it down into place values:
- 3 hundreds, 6 tens, and 8 ones
As a single number:
- 368
As a sum of its place values:
- 300 + 60 + 8
32 less than 400:
- 32 less than 400 is 368
As a subtraction from a nearby higher number:
- 400 - 32
By understanding these different representations, you can see how the number 456 can be expressed in multiple ways, making it easier to understand its value and position within different contexts.
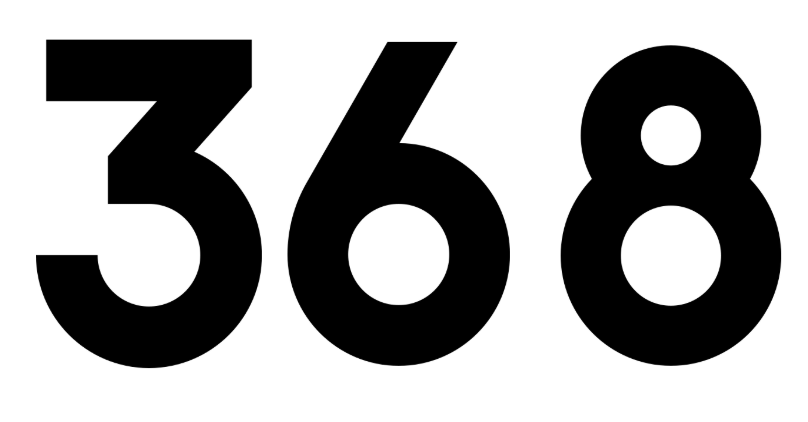
What Are Number Patterns?
Number patterns are sequences of numbers that follow a specific rule or set of rules. These rules can involve adding or subtracting a certain number repeatedly to get the next number in the sequence.
Example 1: Adding 20 each time or Skip by 20
- Starting number: 450
- Rule: Add 20
Sequence: 450, 470, 490, 510, 530, 550, ...
Here's how it works:
- Start with 450.
- Add 20 to 450 to get 470
- Add 20 to 470 to get 490
- Add 20 to 490 to get 510
- Continue this pattern to get the next numbers.
Example 2: Adding 50 each time or Skip by 50
- Starting number: 300
- Rule: Add 50
Sequence: 300, 350, 400, 450, 500, 550, ...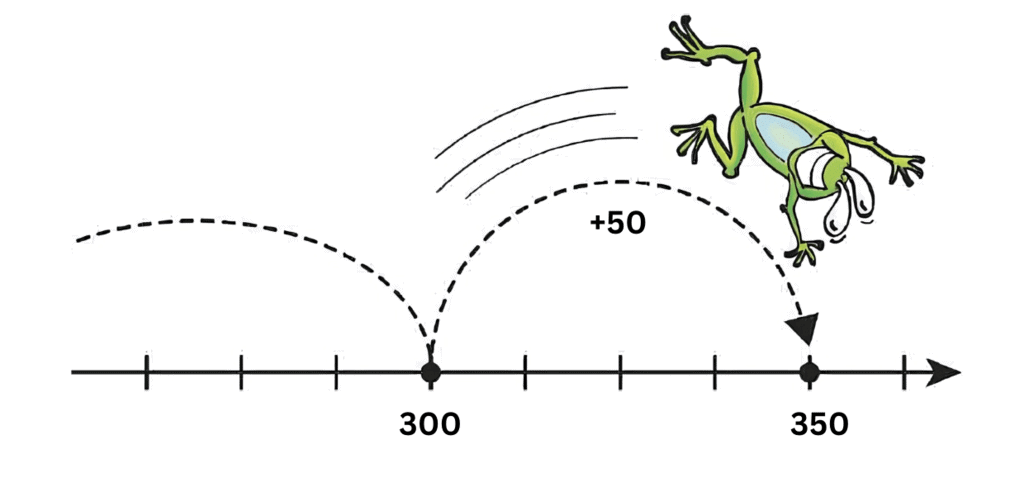
Here's how it works:
- Start with 300.
- Add 50 to 300 to get 350
- Add 50 to 350 to get 400
- Add 50 to 400 to get 450
- Continue this pattern to get the next numbers.
Number Patterns with Subtraction
When creating a number pattern using subtraction with bigger numbers, we'll subtract a fixed number of tens each time to get the next number in the sequence.
Example 1: Subtracting 30 each time
- Starting number: 600
- Rule: Subtract 30
Sequence: 600, 570, 540, 510, 480, 450, ...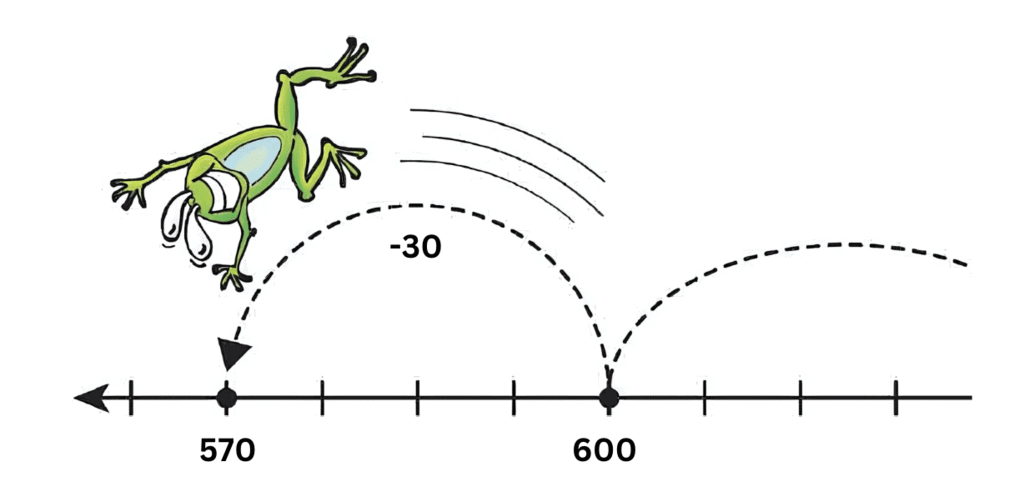
Here's how it works:
- Start with 600.
- Subtract 30 from 600 to get 570
- Subtract 30 from 570 to get 540
- Subtract 30 from 540 to get 510
- Continue this pattern to get the next numbers.
Example 2: Subtracting 40 each time
- Starting number: 800
- Rule: Subtract 40
Sequence: 800, 760, 720, 680, 640, 600, ...
Here's how it works:
- Start with 800.
- Subtract 40 from 800 to get 760
- Subtract 40 from 760 to get 720
- Subtract 40 from 720 to get 680
- Continue this pattern to get the next numbers.
Identifying the Rule in Larger Number Patterns
To identify the rule in a number pattern with larger numbers, look at the differences between consecutive numbers:
Example 1: Pattern: 450, 470, 490, 510, 530, ...
- Find the difference between each pair of numbers:
- 470 - 450 = 20
- 490 - 470 = 20
- 510 - 490 = 20
- 530 - 510 = 20
The rule here is to add 20 each time.
Example 2: Pattern: 900, 870, 840, 810, 780, ...
Find the difference between each pair of numbers:- 900 - 870 = 30
- 870 - 840 = 30
- 840 - 810 = 30
- 810 - 780 = 30
The rule here is to subtract 30 each time.

Creating Your Own Patterns
You can create your own number patterns with larger numbers by choosing a starting number and a rule (either addition or subtraction by tens). For example:
Starting number: 650, Rule: Add 40
- Sequence: 650, 690, 730, 770, 810, ...
Starting number: 1000, Rule: Subtract 50
- Sequence: 1000, 950, 900, 850, 800, ...
By understanding and practicing number patterns with addition and subtraction using larger numbers, you'll be able to recognize and create sequences that follow specific rules.

Learn with Story
Once upon a time in the town of Mathville, there lived a young detective named Noah. Noah was not an ordinary detective; he was a number detective, solving mysteries using his keen understanding of numbers and patterns.
One sunny day, Noah received a mysterious letter with a series of number riddles. Each riddle presented a clue about a specific number, and Noah's task was to decipher these clues and find the hidden numbers. Excited for the challenge, Noah put on his detective hat and got to work.
Riddle 1: "I have 2 zeroes as digits and am very close to 99."
Noah quickly realized that a number with two zeroes and close to 99 had to be 100. The zeroes in 100 act as placeholders, making it very close to 99.
Riddle 2: "I have 1 nine as a digit and is just 2 less than 300."
This clue pointed to the number 298. It has one zero in the tens place and is just 2 less than 300.

Riddle 3: "I have 2 hundreds, 9 tens, and 8 ones."
Noah recognized this as the number 298, as it has 2 hundreds (200), 9 tens (90), and 8 ones (8).

Riddle 4: "I have 2 tens and 5 ones, I am between 500 and 550, and my hundreds digit is 5."
This described the number 525. It has 5 tens and 2 ones, is between 500 and 550, and the hundreds digit is 5.

Noah continued solving each riddle with enthusiasm, using his knowledge of place value and number sense to crack the codes. After solving all the riddles, he realized that the final mystery number was hidden in a clue about centuries and half centuries.
Riddle 5: "I am century + half century."
This clue referred to the number 150. A century is 100, and half a century is 50. When you add them together, you get 150.
Noah felt proud of his detective skills and decided to share his solutions with the people of Mathville.
You can also solve the number riddles just by understanding numbers more.

Making numbers
To create a number in the hundreds using different numbers, we can break down the number into its place values and then fill in the blanks with appropriate numbers. Let's use the example of making the number 789 using six different numbers:
Identify the Place Values of the Number:
- Hundreds place: 700
- Tens place: 80
- Ones place: 9
Fill in the Blanks with Different Numbers:
- To make 700, we can use 300 + 200 + 200
- To make 80, we can use 40 + 40
- To make 9, we can use 4 + 4 + 1
Putting these numbers together:
- 9=4+4+1
So, to create the number 789 using six different numbers, we can use: 300+200+200+40+40+4+4+1=789
This breakdown shows how we can represent a number in hundreds using various numbers that add up to the desired value. You can do similar to all numbers.
In summary, we explored how numbers can be represented in various ways and learned about number patterns. We also discussed how to create number patterns using operations such as addition and subtraction. You are encouraged to try additional examples to deepen your understanding and become more familiar with these concepts.
Let's Practice
Question 1: Milin and Aditya are resting. Shubh asks them to complete the number patterns. Let us help them fill in the empty boxes.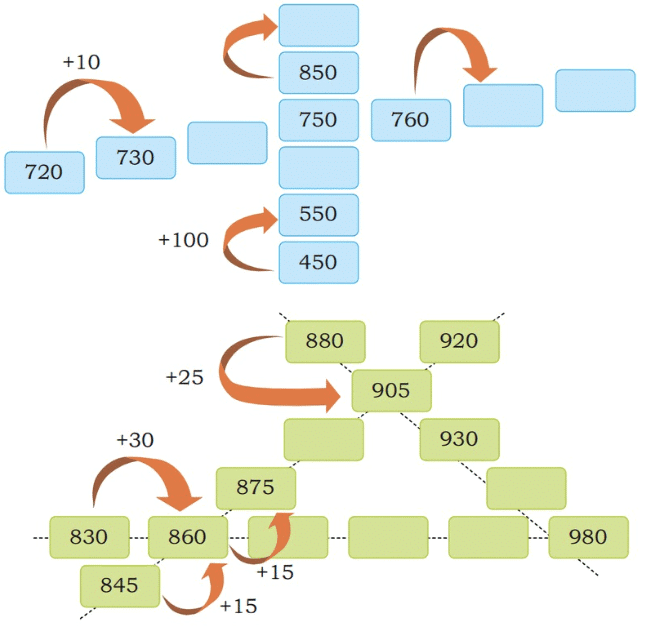
 View Answer
View Answer 
|
26 videos|180 docs|28 tests
|
FAQs on House of Hundreds - II Chapter Notes - Mathematics for Class 3 (Maths Mela)
| 1. What are the different ways to represent numbers in math? |  |
| 2. How can we identify number patterns in subtraction? |  |
| 3. What is a number pattern and why is it important? |  |
| 4. How do you find the rule in a larger number pattern? |  |
| 5. Can you explain the concept of 'House of Hundreds' in relation to number patterns? |  |
















