Compound Interest | Mathematics for GCSE/IGCSE - Year 11 PDF Download

Compound Interest

• Compound interest is when interest is paid on both the original amount and the interest accumulated from previous periods.
• This contrasts with simple interest, where interest is only calculated on the original amount.
  • Simple interest increases by the same amount each period, while compound interest increases by a progressively larger amount each period.

How do you work with compound interest?

• Keep multiplying by the decimal equivalent of the percentage you want (the multiplier, p)
• A 25% increase (p = 1 + 0.25) each year for 3 years is the same as multiplying by 1.25 × 1.25 × 1.25
  • Using powers, this is the same as × 1.25³
• In general, the multiplier p applied n times gives an overall multiplier of pⁿ
• If the percentages change varies from year to year, multiply by each one in order
  • a 5% increase one year followed by a 45% increase the next year is 1.05 × 1.45
• In general, the multiplier p₁ followed by the multiplier p₂ followed by the multiplier p₃... etc gives an overall multiplier of p₁p₂p₃... 

Compound interest formula

• Alternative method: A formula for the final ("after") amount is 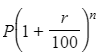where...
• ...P is the original ("before") amount, r is the % increase, and n is the number of years
• Note that 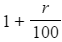 is the same value as the multiplier

Depreciation

• Depreciation is the process by which an item loses value over time.
• Examples include cars, game consoles, and other electronics.
• Depreciation is typically calculated as a percentage decrease at the end of each year.
• This calculation works similarly to compound interest, but it involves a percentage decrease instead of an increase.

How do I calculate a depreciation?

• You would calculate the new value after depreciation using the same method as compound interest
  • Identify the multiplier, p (1 - "% as a decimal")
    • 10% depreciation would have a multiplier of p = 1 - 0.1 = 0.9
    • 1% depreciation would have a multiplier of p = 1 - 0.01 = 0.99
  • Raise the multiplier to the power of the number of years (or months etc) pⁿ
  • Multiply by the starting value
• New value is A x pⁿ
  • A is the starting value
  • p is the multiplier for the depreciation 
  • n is the number of years
• Alternative method: A formula for the final ("after") amount is 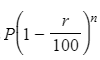 where...   
  • ...P is the original ("before") amount, r is the % decrease, and n is the number of years
• If you are asked to find the amount the value has depreciated by:
  • Find the difference between the starting value and the new value