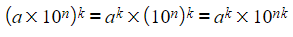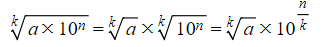Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Standard Form
Standard Form | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Converting To & From Standard Form
What is standard form?
- Standard Form (sometimes called Standard Index Form) is a way of writing very big and very small numbers using powers of 10
Why do we use standard form?
Writing big (and small) numbers in Standard Form allows us to:
- write them more neatly
- compare them more easily
- make things easier when doing calculations
How do we use standard form?
- Numbers in standard form are always written in the form
a x 10n - The rules:
- 1 ≤ a < 10 so there is one non-zero digit before the decimal point
- n > 0 for LARGE numbers – how many times a is multiplied by 10
- n < 0 for SMALL numbers – how many times a is divided by 10
- Calculations involving standard form can be done using a calculator, if permitted.
Operations with Standard Form
How do I multiply or divide two numbers in standard form?
- When multiplying or dividing two numbers in standard form:
- If feasible, utilize a calculator for accuracy.
- Otherwise, begin by multiplying or dividing the number parts.
- If the result is less than 1 or greater than 10, express it in standard form.
- For instance:
- 4 × 5 = 20 = 2 × 101
- 2 ÷ 4 = 0.5 = 5 × 10-1
- Proceed by multiplying or dividing the powers of 10 as per the laws of indices.
- Multiply the two parts together to obtain the final answer in standard form.
- Further application of the laws of indices may be necessary, for example:
- 4 × 102 × 5 × 107 = 2 × 101 × 109 = 2 × 1010
How do I add or subtract two numbers in standard form?
- If you can, use a calculator!
- If you need to add or subtract numbers in standard form, ensure they have the same power of 10.
- If the powers of 10 are equal, you can directly add or subtract the numerical parts.
- If the result is not between 1 and 10, convert it back to standard form.
- For example, 7 × 105 - 6.2 × 105 = 0.8 × 105 = 8 × 104.
- If the powers of 10 differ, adjust the numbers to have the same power by choosing the larger one.
- For instance, 7 × 105 + 6 × 104 = 7 × 105 + 0.6 × 105 = 7.6 × 105
- If dealing with small powers of 10, it might be easier to convert numbers to regular form before performing operations.
- Use a calculator whenever possible for accuracy and efficiency.
How do I find powers or roots of a number in standard form?
- Use a calculator whenever possible for complex calculations.
- Standard form involves two terms multiplied together; split the power or root for easier computation.
- Always check if the final answer needs to be in standard form.
The document Standard Form | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
42 videos|395 docs|19 tests
|
FAQs on Standard Form - Mathematics for GCSE/IGCSE - Class 10
| 1. How do you convert a number to standard form? |  |
Ans. To convert a number to standard form, you need to express it as a number between 1 and 10 multiplied by a power of 10. For example, the number 450,000 in standard form would be written as 4.5 x 10^5.
| 2. What is the purpose of using standard form in mathematics? |  |
Ans. Standard form is used in mathematics to represent very large or very small numbers in a more concise and manageable way. It allows for easier comparison and calculation of numbers with different magnitudes.
| 3. How do you perform operations with numbers in standard form? |  |
Ans. To add or subtract numbers in standard form, you must ensure that the powers of 10 are the same. For multiplication and division, you multiply or divide the coefficients and add or subtract the exponents.
| 4. Can you convert a number from standard form back to its original form? |  |
Ans. Yes, you can convert a number from standard form back to its original form by multiplying the coefficient by the power of 10 raised to the exponent. For example, 3.2 x 10^6 would be converted back to 3,200,000.
| 5. Why is it important to understand how to work with standard form in exams? |  |
Ans. Understanding how to work with standard form is important in exams because it allows you to efficiently handle numbers of varying magnitudes and perform calculations accurately. It demonstrates a strong grasp of mathematical concepts and problem-solving skills.
Related Searches