Notes: Ratio & Proportion | Mathematics & Pedagogy Paper 2 for CTET & TET Exams - CTET & State TET PDF Download
| Table of contents |

|
| Ratios |

|
| Proportions |

|
| Introduction to Direct and Inverse Proportions |

|
| Methods to solve Direct Proportion Problems |

|
| Inverse Proportion |

|
Ratio and proportion are fundamental in mathematics, helping compare quantities and understand relationships between values. They are essential topics in CTET, TET, and other educational exams.
This document provides a detailed overview of key concepts, including the properties, applications, and problem-solving techniques of ratio and proportion, crucial for effective math teaching and exam success.
Ratios
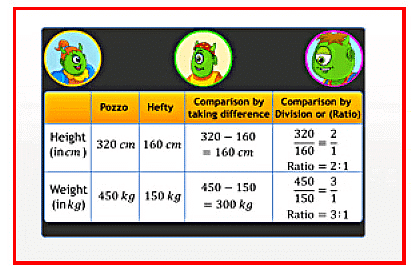
- Usually, the comparison of quantities of the same type can be made by the method of difference between the quantities. However, a more meaningful comparison between the quantities can be made by using division, i.e. by verifying how many times one quantity is into the other quantity. This method is known as comparison by ratio.
For Example: Keertana's weight is 20 kg and her father's weight is 80 kg. So we can say that Keertana's father's weight and Keertana's weight are in the ratio 20 : 80. - To calculate ratio, the two quantities have to be measured using the same unit. If not, they should be converted to the same unit before ratio is taken. The same ratio can occur in different situations.
For Example: The ratio 4 : 5 is different from 5 : 4.
Thus, the order in which the quantities are taken into consideration to express their ratio is important. - A ratio can be treated as a fraction.
Difference between fractions and ratios
- A fraction describes a part of a whole and its denominator represents the total number of parts.
Example: In the fraction 1/3, it means one part out of three equal parts. - Ratios, on the other hand, are used to compare two different quantities or amounts. They show the relative size of one quantity to another.
Example: In a society, 10 people like driving, 20 people like swimming and the total number of people in society is 30.
i) The ratio of the number of people liking driving to the total number of people = 10 : 30.
ii) The ratio of the number of people liking swimming to the number of people liking driving is 20 : 10.
Equivalent Ratios
When the given ratios are equal, then these ratios are called as equivalent ratios.
- Equivalent ratios can be obtained by multiplying and dividing the numerator and denominator with the same number.
Example: Ratios 10 : 30 (=1 : 3) and 11 : 33 (=1 : 3) are equivalent ratios. - To calculate equivalent ratio, convert the ratio into a fraction, and then multiply or divide the numerator and the denominator by the same number.
For Example: 4 : 5 is equivalent to 8 : 10 or 12 : 15 and so on. A ratio can be expressed in its lowest form. For example, the ratio 45 : 25 in its lowest form can be written as follows: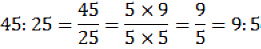 Thus, the lowest form of 45 : 25 is 9 : 5.
Thus, the lowest form of 45 : 25 is 9 : 5.
Unitary Method
The method in which first we find the value of one unit and then the value of required number of units is known as Unitary Method.
Example: Cost of two shirts in a shop is Rs.200. What will be the cost of 5 shirts in the shop?
Solution : Cost of 2 shirts = Rs.200
⇒ Cost of 1 shirt = 200/2 = 100
⇒ Cost of 5 shirts = (200/2) ∗ 5 = 100 ∗ 5
= Rs.500
Proportions

- Proportions are a way to express the equality of two ratios. If the ratio of Quantity A to Quantity B is the same as the ratio of Quantity C to Quantity D, then these quantities are said to be in proportion.
- This relationship is indicated using the symbols "?" or "=". For instance, the quantities 4, 16, 5, and 20 are in proportion, while 4, 20, 5, and 16 are not. In the proportion a : b ? c : d, a and d are referred to as the extreme terms, while b and c are the middle terms.
- The unitary method involves finding the value of a single unit and then using that value to determine the total for multiple units.
Example
- Imagine the cost of 8 bags is Rs. 240. To find out the cost of 6 bags using the unitary method, we first calculate the cost of one bag:
- Rs. 240 divided by 8 equals Rs. 30.
- Now, to find the cost of 6 bags: 6 × Rs. 30 = Rs. 180.
- Therefore, the cost of 6 bags is Rs. 180.
Introduction to Direct and Inverse Proportions
There are so many situations in our life where we see some direct or indirect relationship between two things. For Instance
If the number of things purchased is increasing then the amount to pay will also increase.
If the speeds of the car will increase then the time to reach the destination will decreases.
Variations
If the value of two objects depends upon each other in such a way that the increase or decrease in the value of one object affects the value of another object then these two objects are said to be in variation.
Direct Proportion
Two quantities a and b are said to be in direct proportion if
Increase in a increases the b
Decrease in a decreases the b
But the ratio of their respective values must be the same.
a and b will be in direct proportion if a/b = k(k is constant) or a = kb.
In such a case if b1, b2 are the values of b corresponding to the values a1, a2 of a respectively then, a1/b2 = a2/b1
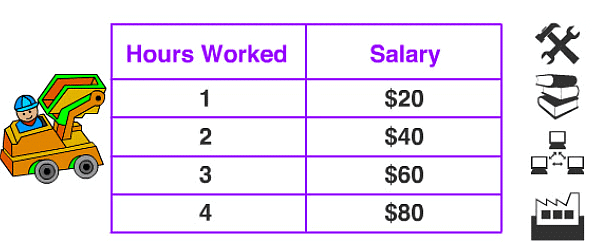
This shows that as the no. of hours worked will increase the amount of salary will also increase with the constant ratio.
Symbol of Proportion

When two quantities a and b are in proportion then they are written as a ∝ b where ∝ represents “is proportion to”.
Methods to solve Direct Proportion Problems
There are two methods to solve the problems related to direct proportion-
1. Tabular Method
As we know that,
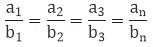
so, if one ratio is given then we can find the other values also. (The ratio remains the constant in the direct proportion).
Example: The cost of 4-litre milk is 200 Rs. Tabulate the cost of 2, 3, 5, 8 litres of milk of same quality.
Solution:
Let X litre of milk is of cost Y Rs.
We know that as the litre will increase the cost will also increase and if the litre will decrease then the cost will also decrease.
Given,
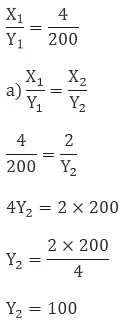
So the cost of 2 ltr milk is 100 Rs.
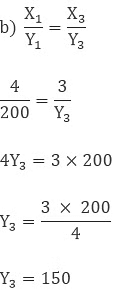
So the cost of 3 ltr milk is 150 Rs.
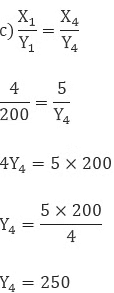
So the cost of 5 ltr milk is 250 Rs.
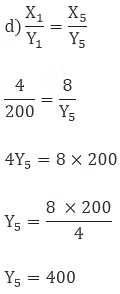
So the cost of 8 ltr milk is 400 Rs.
2. Unitary Method
If two quantities a and b are in direct proportion then the relation will be
k = a/b or a = kb
We can use this relation in solving the problem.
Example: If a worker gets 2000 Rs. to work for 4 hours then how much time will they work to get 60000 Rs.?
Solution:
Here,
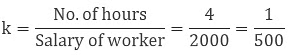
By using this relation a = kb we can find
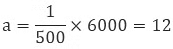
Hence, they have to work for 12 hours to get 60000 Rs.
Inverse Proportion
Two quantities a and b are said to be in Inverse proportion if
Increase in a decreases the b
Decrease in a increases the b
But the ratio of their respective values must be the same.
a and b will be in inverse proportion if k= ab
In such a case if b1, b2 are the values of b corresponding to the values a1, a2 of a respectively then, a1b1 = a2b2 = k,
When two quantities a and b are in inverse proportion then they are written as a ∝ 1/b

This shows that as the distance of the figure from light increases then the brightness to the figure decreases.
Example: If 15 artists can make a statue in 48 hours then how many artists will be required to do the same work in 30 hours?
Solution:
Let the number of artists required to make a statue in 30 hours be y.
We know that as the no. of artists will increase the time to complete the work will reduce. So, the number of hours and number of artists are in inverse proportion.
So 48 × 15 = 30 × y (a1b1 = a2b2)
Therefore,
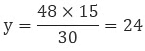
So, 24 artists will be required to make the statue in 30 hours.
|
82 videos|273 docs|69 tests
|
FAQs on Notes: Ratio & Proportion - Mathematics & Pedagogy Paper 2 for CTET & TET Exams - CTET & State TET
| 1. What is the difference between direct and inverse proportions? |  |
| 2. How can I solve problems involving direct proportions? |  |
| 3. Can you give an example of an inverse proportion problem? |  |
| 4. What are some real-life applications of ratios and proportions? |  |
| 5. How do you set up a proportion from a word problem? |  |




















