Detailed Notes: Quadratic Equations | Mathematics (Maths) for JEE Main & Advanced PDF Download
What are Quadratic Equations?
- A quadratic polynomial expression equated to zero becomes a quadratic equation
- The values of x that satisfy the equation are called roots/ zeros of the Quadratic Equation.
- General form: ax2 + bx + c = 0, where a, b, c are real numbers, and a ≠ 0, the numbers a, b, and c are called the coefficients of the equation.
a is called the leading coefficient, b is called the middle coefficient, and c is called the constant term.
Examples: 3x2 + x + 5 = 0,-x2 + 7x + 5 = 0, x2 + x = 0, x2 = 0.
Factor and Remainder Theorem
Remainder Theorem
- The Remainder theorem states that when a polynomial p(x) is divided by a linear polynomial (x - a), then the remainder is equal to p(a)
- Consider f(x) = (x - r)q(x) + R.
- If you divide a polynomial f(x) by (x - c), the remainder of that division is equal to f(c).
Example: Use the remainder theorem to find the remainder when f(x) = 3x2 + 5x - 8 is divided by (x - 2)
Sol: Use the Remainder Theorem.
Put x = 2 in f(x). Since we are dividing f(x) = 3x2 + 5x - 8 by (x - 2), we consider x = 2.
Hence, the remainder R is given by:
R = f(2) = 3(22) + 5(2) - 8 = 14
Factor Theorem
- The Factor Theorem is a special case of the Remainder Theorem and is used to determine whether a given polynomial has a specific factor.
- If f(x) is a polynomial and (x - c) is a factor of f(x), then f(c) = 0.
- In other words:
If you substitute x = c into the polynomial f(x) and the result is 0, then (x - c) is a factor of f(x).
Example: Use the factor theorem to decide if (x - 2) is a factor of f(x) = x5 - 2x4 + 3x3 - 6x2 - 4x + 8.
Sol: We know that (x - r) will be a factor of f(x) if f(r) = 0. Therefore, by using this condition, we can decide whether (x - 2) is a factor of the given polynomial or not.
f(x) = x5 - 2x4 + 3x3 - 6x2 - 4x + 8.
f(2) = (2)5 - 2(2)4 + 3(2)3 - 6(2)2 - 4(2) + 8 = 0Since f(2) = 0, we can conclude that (x - 2) is a factor.
Roots of an Equation
- The values of variables satisfying the given equation are called its roots
- In other words, x = α is a root of the equation f(x), if f(α) = 0. The real roots of an equation f(x) = 0 are the x-coordinates of the points where the curve y = f(x) intersects the x-axis.
- Example: x2 - 3x + 2 = 0. At x = 1 and 2, the equation becomes zero.
- When referring to the zeroes of ax2+ bx + c, it usually means the roots of the equation ax2+ bx + c
Did You Know
A polynomial can be rewritten as given below:
y = a(x - r1)(x - r2)....(x - rn)
The factors like (x - r1) are called linear factors because they describe a line when you plot them.
Example: What values of x satisfy the equation 2x2 = 18?
Sol: 2x2 = 18
2x2 / 2 = 18 / 2
x2 = 9
√(x2) = √9
x = ±3
The following values of x satisfy the equation 2x2 = 18:
-3 and 3
Methods of Solving Quadratic Equations
There are two methods to solve a Quadratic equation
- Algebraic Method
- Graphical Method (Absolute)
Now we will discuss each method in detail to analyze the method to calculate roots
Algebraic Method
- As we have already done the middle-term splittin method but not every quadratic equation can be splitter into its respective factors
- Therefore we will use the Discriminant method prominently to solve equations
- The roots of a quadratic equation ax2+ bx + c = 0 are given by the quadratic formula:
x = (-b ± √(b2 - 4ac)) / 2a
The term under the square root, b2 - 4ac, is called the discriminant (Δ)
Did You Know
Let If α and β are the roots of a quadratic equation ax2+ bx + c and we have to calculate the sum and product of roots then
Sum of roots = - b/a
Product of roots = c/a
Nature of Roots
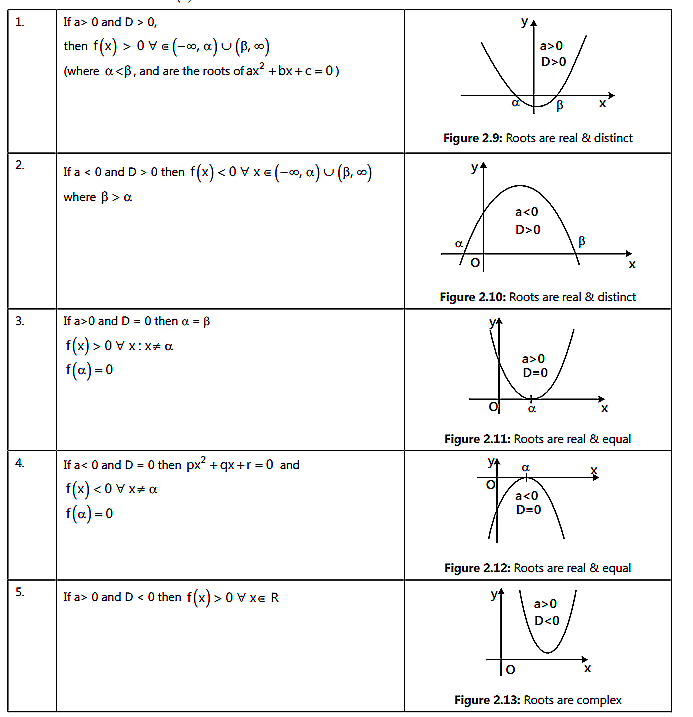
Consider the quadratic equation ax2+ bx + c = 0 where and . The roots can be determined using the quadratic formula: The nature of the roots depends on the value of (Discriminant):- D > 0: The roots are real and distinct (unequal).
- : The roots are real and coincident (equal).
- D < 0: The roots are complex (imaginary).
- If one root is , the other is its conjugate (where and ).

Very Important Conditions
- If y = ax2 + bx + c is positive for all real values of x, then a > 0 and D < 0.
- If y = ax2 + bx + c is negative for all real values of x, then a < 0 and D < 0.
- If both roots are infinite for the equation ax2 + bx + c = 0,
x = 1 / y ⇒ (a / y2) + (b / y) + c = 0.- cy2 + by + a = 0
(- b / c) = 0, (a / c) = 0 ⇒ a = 0, b = 0, and c ≠ 0.The equations a1x2 + b1x + c1 and a2x2 + b2x + c2 have the following conditions:
1. One common root if:
(b1c2 - b2c1) / (c1a2 - c2a1) = (c1a2 - c2a1) / (a1b2 - a2b1)
2. Both roots common if:
a1/a2 = b1/b2 = c1/c2
 |
Download the notes
Detailed Notes: Quadratic Equations
|
Download as PDF |
Roots in Particular Cases
For the quadratic equation ax2 + bx + c = 0:
(a) If b = 0, ac < 0 ⇒ Roots are of equal magnitude but of opposite sign
(b) If c = 0 ⇒ One root is zero, the other is -b/a;
(c) If b = c = 0 ⇒ Both roots are zero;
(d) If a = c ⇒ The roots are reciprocal to each other;
(e) If (a > 0; c < 0) or (a < 0; c > 0) ⇒ The roots are of opposite signs;
(f) If the sign of a = sign of b × sign of c ⇒ The root of greater magnitude is negative;
(g) If a + b + c = 0 ⇒ One root is 1 and the other is c/a;
(h) If a = b = c = 0, then the equation will become an identity and will be satisfied by every value of x.
Did You Know
If you have to find the maximum and minimum value of a quadratic equation ax2 + bx + cWrite the quadratic equation ax2 + bx + c into a * [(x + b / 2a)² - D / 4a²] , where D = b2 - 4ac
If a > 0:
- The equation has a minimum value of (4ac - b²) / 4a at x = -b / 2a.
- There is no maximum value.
If a < 0:
- The equation has a maximum value of (4ac - b²) / 4a at x = -b / 2a.
- There is no minimum value.
Solved Examples: Algebraic Method
Example 1: Form a quadratic equation with real coefficients when one root is 3 - 2i.
Sol: Since the complex roots always occur in pairs, so the other root is 3 + 2i.
Therefore, we can form the required quadratic equation by obtaining the sum and product of the roots.The sum of the roots is:
(3 + 2i) + (3 - 2i) = 6.The product of the roots is:
(3 + 2i) × (3 - 2i) = 9 - 4i2 = 9 + 4 = 13.Hence, the equation is x2 - Sx + P = 0.
⇒ x2 - 6x + 13 = 0.
Example 2: Consider the quadratic polynomial f(x) = x2 - px + q where f(x) = 0 has prime roots. If p + q = 11 and a = p2 + q2, then find the value of f(a) where a is an odd positive integer.
Sol: Here f(x) = x2 - px + q, hence by considering α and β as its roots and using the formulae for sum and product of roots and the given conditions, we get the values of f(a).
f(x) = x2 - px + q
Given α and β are prime:
α + β = p ...(i)
αβ = q ...(ii)Given p + q = 11 ⇒ α + β + αβ = 11
⇒ (α + 1)(β + 1) = 12; α = 2, β = 3 are the only primes that solve this equation.∴ f(x) = (x - 2)(x - 3) = x2 - 5x + 6
∴ p = 5, q = 6 ⇒ a = p2 + q2 = 25 + 36 = 51;
f(51) = (51 - 2)(51 - 3) = 49 × 48 = 3422
Example 3: If a Quadratic equation (QE) is formed from y2 = 4ax and y = mx + c and has equal roots, then find the relation between c, a, and m.
Sol: By solving these two equations, we get the quadratic equation; and as it has equal roots, hence D = 0.
(mx + c)2 = 4ax;
m2x2 + 2(cm - 2a)x + c2 = 0
Given that the roots are equal. So, D = 0 ⇒ 4(cm - 2a)2 ⇒ 4c2m2
⇒ 4a2 = 4acm
a = cm ⇒ c = a/m
This is a condition for the line y = mx + c to be a tangent to the curve y2 = 4ax.
Graphical Method
As we are talking about Quadratic Equations,
- The graph of a quadratic equation ax2+ bx + c = 0 will always be a Parabola with vertex (-b/2a, -D/2a)
- Graph Shape:
a > 0: Parabola opens upwards (concave up).
a < 0: Parabola opens downwards (concave down). - Graph Categories:
1. Two real roots a and b where a < b:
ax2 + bx + c > 0 for x ∈ (-∞, a) ∪ (b, ∞),
ax2 + bx + c < 0 for x ∈ (a, b).
2. One real root a = b:
ax2 + bx + c = 0 for x = a.
3. No real roots:
ax2 + bx + c > 0 for x ∈ R (a > 0),
ax2 + bx + c < 0 for x ∈ R (a < 0).
- Some Important Cases are given below,
Solved Examples: Graphical Method
Example 1: The graph of a quadratic polynomial y = ax2 + bx + c is as shown in the figure below. Comment on the sign of the following quantities.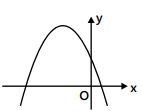
(A) b - c
(B) bc
(C) c - a
(D) ab2
Sol: Some observations from the graph are
Direction of the parabola:
- If it opens upward → a > 0.
- If it opens downward → a < 0.
Y-intercept:
- The point where the graph crosses the y-axis is (0, c).
- If the intercept is above the origin → c > 0.
- If it is below the origin → c < 0.
Vertex position:
- The vertex is at (-b/2a, constant term).
- If the vertex is left of the y-axis → -b/2a < 0.
- If the vertex is right of the y-axis → -b/2a > 0.
The slope at the y-intercept:
- The derivative dy/dx = 2ax + b.
- At x = 0, the slope is b. If the graph is rising at x = 0 → b > 0. If falling → b < 0.
- Here a < 0
- (-b/a) < 0 ⇒ b < 0; c > 0.
- As b - c = (-ve) - (+ve), it must be negative;
- Also, bc = (-ve)(+ve); this must be negative;
- Then, β + (1/α) = (-ve) + (+ve); the product must be negative; finally,
- c - a = (+ve) - (-ve), it must be positive.
Example 2: Suppose the graph of a quadratic polynomial y = x2 + px + q is situated so that it has two arcs lying between the rays y = x and y = 2x, x ≥ 0. These two arcs are projected onto the x-axis yielding segments SL and SR, with SR to the right of SL. Find the difference of the length (SR) - (SL).
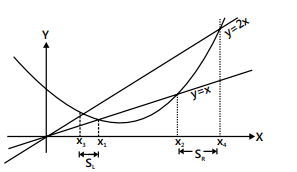
Sol: Let the roots of x2 + px + q = x be x1 and x2, and the roots of x2 + px + q = 2x be x3 and x4.
SR = x4 - x2 and SL = x1 - x3
⇒ SR - SL = x4 + x3 - x1 - x2.∴ |(SR) - (SL)| = |[-(p - 2) - {-(p - 1)}]| = 1.
|
209 videos|447 docs|187 tests
|
FAQs on Detailed Notes: Quadratic Equations - Mathematics (Maths) for JEE Main & Advanced
| 1. What is a quadratic equation and how can it be identified? |  |
| 2. What is the Factor Theorem and how does it relate to quadratic equations? |  |
| 3. What are the methods for solving quadratic equations? |  |
| 4. Can you explain the graphical method for solving quadratic equations with an example? |  |
| 5. What are some common mistakes to avoid when solving quadratic equations? |  |