Q1: Simplified form of the Boolean function:
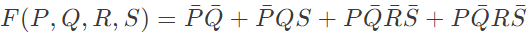 is (2024)
is (2024)
(a) 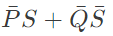
(b) 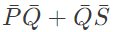
(c) 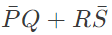
(d) 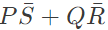
Ans: (a)
Sol: 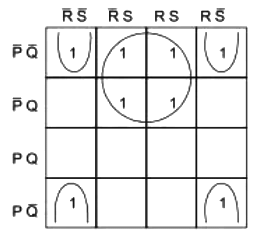 Minimize function =
Minimize function = 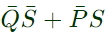
Q2: The output expression for the Karnaugh map shown below is (2019)
 (a)
(a) 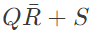
(b) 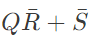
(c) QR + S
(d) 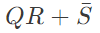
Ans: (a)
Sol:
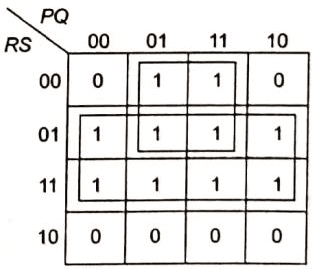 Output =
Output =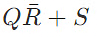
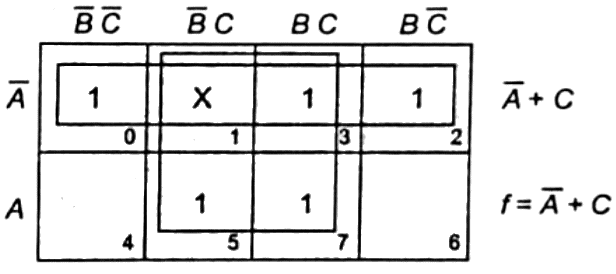
Q3: Digital input signals A, B, C with A as the MSB and C as the LSB are used to realize the Boolean function
F = m0 + m2 + m3 + m5 + m7, where mi
denotes the ith minterm. In addition, F has a don't care for m1. The simplified expression for F is given by (2018)
(a) 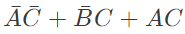
(b) 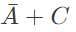
(c) 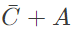
(d) 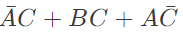
Ans: (b)
Sol: Given, f = m0 + m2 + m3 + m5 + m7 and m1 = don't care
Q4: The output expression for the Karnaugh map shown below is (SET-1(2017))
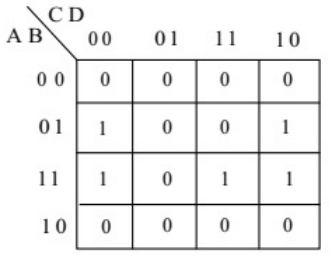 (a)
(a) 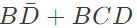
(b) 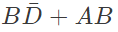
(c) 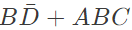
(d) 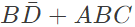
Ans: (d)
Sol: 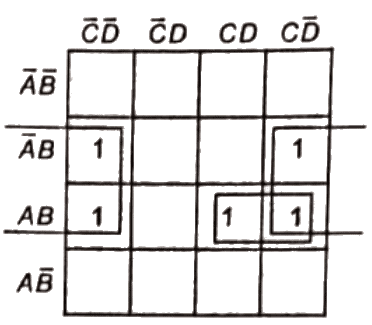
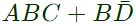
Q5: The Boolean expression 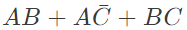 simplifies to (SET-1 (2017))
simplifies to (SET-1 (2017))
(a) 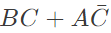
(b) 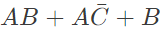
(c) 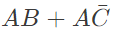
(d) AB + BC
Ans: (a)
Sol: 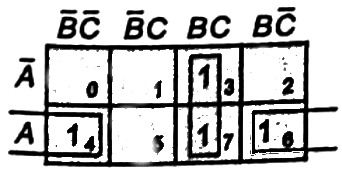
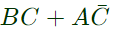
Q6: The Boolean expression 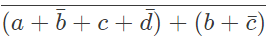 simplifies to (SET-2 (2016))
simplifies to (SET-2 (2016))
(a) 1
(b) 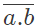
(c) a.b
(d) 0
Ans: (d)
Sol: 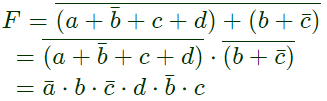 F = 0
F = 0
Q7: The output expression for the Karnaugh map shown below is (SET-2 (2016))
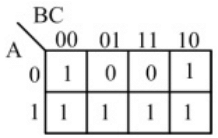 (a)
(a) 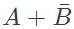
(b) 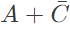
(c) 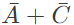
(d) 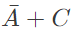
Ans: (b)
Sol: 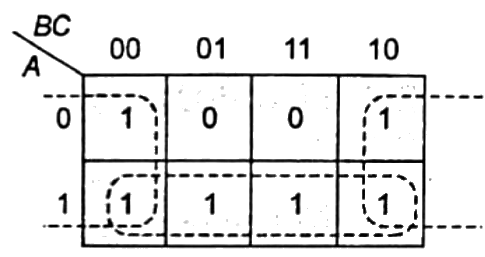
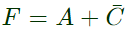
Q8: Consider the following Sum of Products expression, F.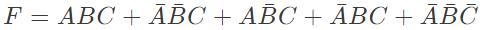 The equivalent Product of Sums expression is (SET-2 (2015))
The equivalent Product of Sums expression is (SET-2 (2015))
(a) 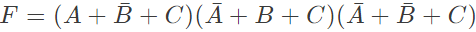
(b) 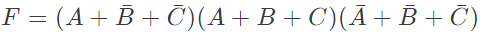
(c) 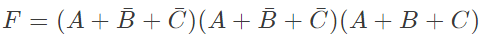
(d) 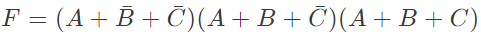
Ans: (a)
Sol: The SOP form of F is ( shown in K-map)
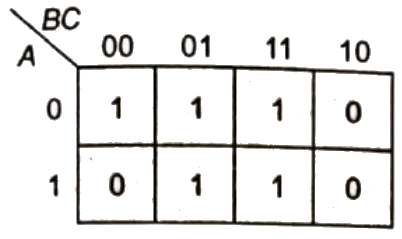 So,POS form can be formed using '0' from the K-map.
So,POS form can be formed using '0' from the K-map.
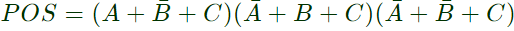
Q9: f(A, B, C, D) = Π M(0, 1, 3, 4, 5, 7, 9, 11, 12, 13, 14, 15) is a maxterm representation of a Boolean function f(A, B, C, D) where A is the MSB and D is the LSB. The equivalent minimized representation of this function is (SET-1 (2015))
(a) 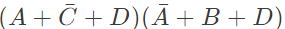
(b) 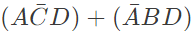
(c) 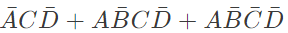
(d) 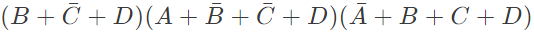
Ans: (a)
Q10: The SOP (sum of products) form of a Boolean function is Σ(0, 1, 3, 7, 11), where inputs are A, B, C , D (A is MSB, and D is LSB). The equivalent minimized expression of the function is (SET-2 (2014))
(a) 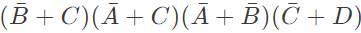
(b) 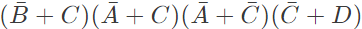
(c) 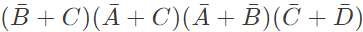
(d) 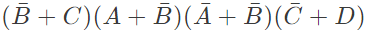
Ans: (a)
Sol: The 4 variable Boolean function is given in canonical sum of product form as,
f(A, B, C, D) = Σ(0, 1, 3, 7, 11)
As the options are given in the simplified product of sum form, we first convert the given function in canonical product of sum form, as under
f(A, B, C, D) = Π(2, 4, 5, 6, 8, 9, 10, 12, 13, 14, 15)
Now by plotting the above function on a 4 variable K-map (Maxterm map), we obtain the simplified expression of the function
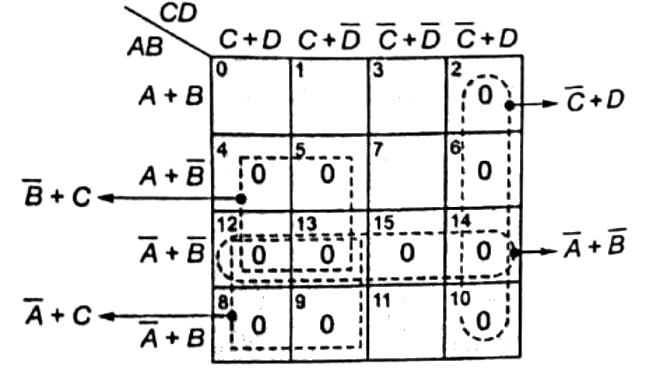
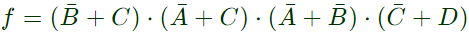
Q11: Which of the following is an invalid state in an 8-4-2-1 Binary Coded Decimal counter (SET-2 (2014))
(a) 1 0 0 0
(b) 1 0 0 1
(c) 0 0 1 1
(d) 1 1 0 0
Ans: (d)
Sol: Binary coded decimal counter counts from 0 to 9. So, 1100 is an initial state i.e. 12.
Q12: In the sum of products function f(X, Y, Z) = ∑(2, 3, 4, 5), the prime implicants are (2012)
(a) 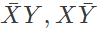
(b) 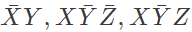
(c) 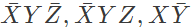
(d) 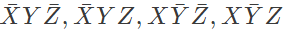
Ans: (a)
Sol: f(X, Y, Z) = Σ(2, 3, 4, 5)
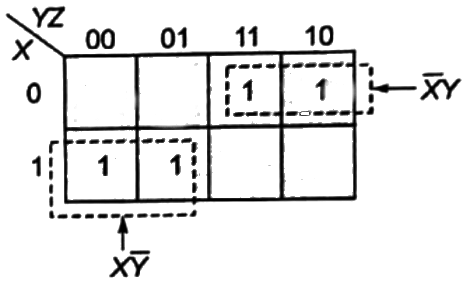
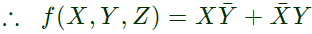
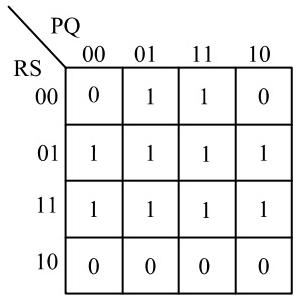
Q13: The following Karnaugh map represents a function F.
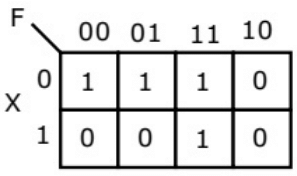 Which of the following circuits is a realization of the above function (2010)
Which of the following circuits is a realization of the above function (2010)
(a) 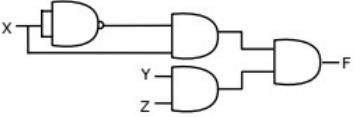 (b)
(b) 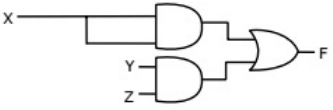 (c)
(c) 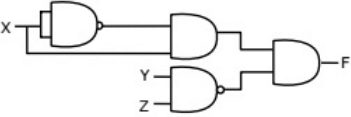 (d)
(d) 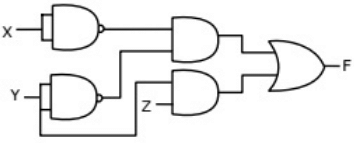 Ans: (d)
Ans: (d)
Sol: From the figure, it is clear that, two NAND gates generate the 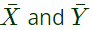 and now two AND gates with i/p
and now two AND gates with i/p 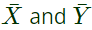 and inputs Y and Z is used to generate two terms of SOP form and OR gate is used to sum them and generate th F.
and inputs Y and Z is used to generate two terms of SOP form and OR gate is used to sum them and generate th F.
Q14: The following Karnaugh map represents a function F.
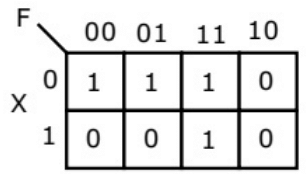 A minimized form of the function F is (2010)
A minimized form of the function F is (2010)
(a) 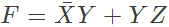
(b) 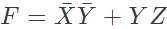
(c) 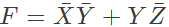
(d) 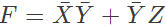
Ans: (b)
Sol:
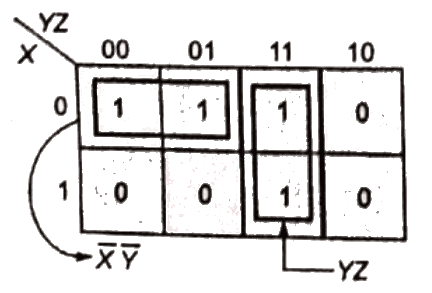
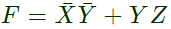
Q15: The simplified form of the Boolean expression 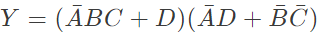 can be written as (2004)
can be written as (2004)
(a) 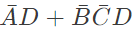
(b) 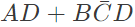
(c) 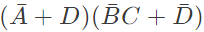
(d) 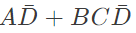
Ans: (a)
Sol: 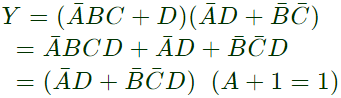
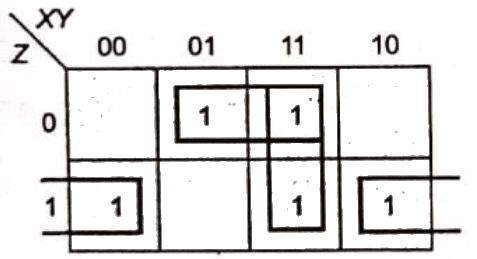
Q16: The boolean expression 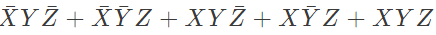 can be simplified to (2003)
can be simplified to (2003)
(a) 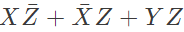
(b) 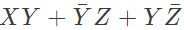
(c) 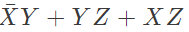
(d) 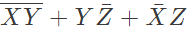
Ans: (b)
Sol: By K-map
 The simplified for is
The simplified for is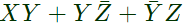 .
.
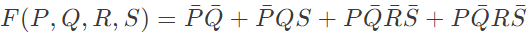 is (2024)
is (2024)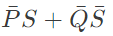
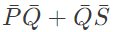
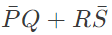
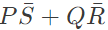
 Minimize function =
Minimize function = 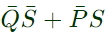
 (a)
(a) 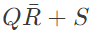
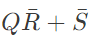
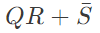
 Output =
Output =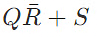
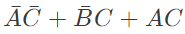
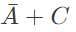
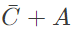
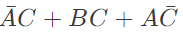

 (a)
(a) 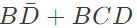
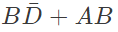
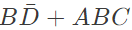
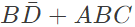

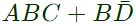
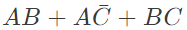 simplifies to (SET-1 (2017))
simplifies to (SET-1 (2017))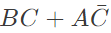
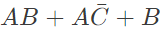
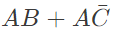

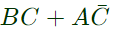
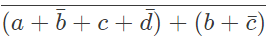 simplifies to (SET-2 (2016))
simplifies to (SET-2 (2016))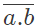
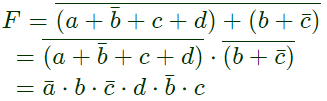 F = 0
F = 0 (a)
(a) 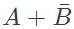
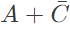
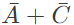
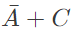

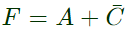
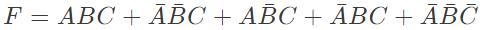 The equivalent Product of Sums expression is (SET-2 (2015))
The equivalent Product of Sums expression is (SET-2 (2015))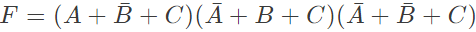
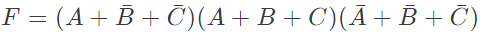
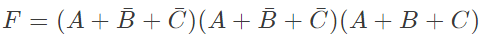
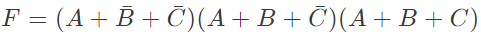
 So,POS form can be formed using '0' from the K-map.
So,POS form can be formed using '0' from the K-map.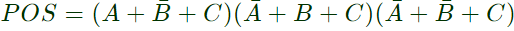
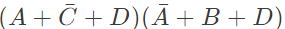
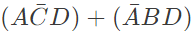
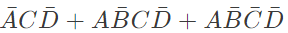
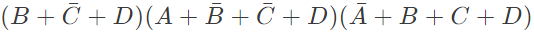
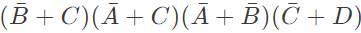
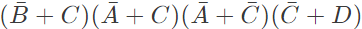
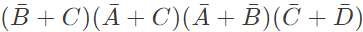
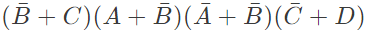

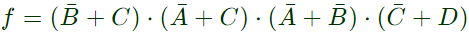
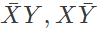
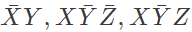
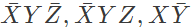
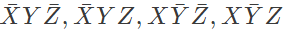

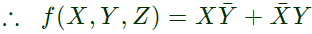
 Which of the following circuits is a realization of the above function (2010)
Which of the following circuits is a realization of the above function (2010) (b)
(b)  (c)
(c)  (d)
(d)  Ans: (d)
Ans: (d)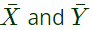 and now two AND gates with i/p
and now two AND gates with i/p 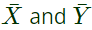 and inputs Y and Z is used to generate two terms of SOP form and OR gate is used to sum them and generate th F.
and inputs Y and Z is used to generate two terms of SOP form and OR gate is used to sum them and generate th F. A minimized form of the function F is (2010)
A minimized form of the function F is (2010)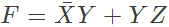
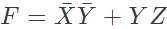
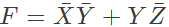
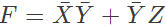

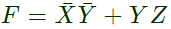
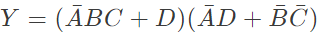 can be written as (2004)
can be written as (2004)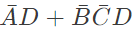
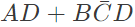
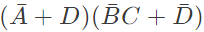
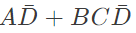
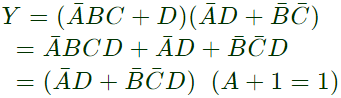
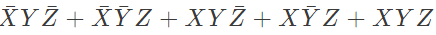 can be simplified to (2003)
can be simplified to (2003)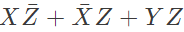
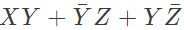
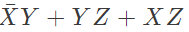
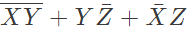
 The simplified for is
The simplified for is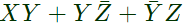 .
.




















