Bayes Theorem | Crash Course for UGC NET Commerce PDF Download
| Table of contents |

|
| Bayes’ Theorem Overview |

|
| What is Bayes’ Theorem? |

|
| Statement of Bayes' Theorem |

|
| Derivation of Bayes' Theorem |

|
| Key Terms Related to Bayes' Theorem |

|
Bayes’ Theorem Overview
Bayes' Theorem is a fundamental concept in probability theory used to determine the conditional probability of an event based on prior knowledge of related conditions. Named after the English statistician Thomas Bayes, who introduced this formula in 1763, Bayes' Theorem is central to the field of statistical inference, known as Bayesian inference.
For instance, suppose we want to calculate the probability that a white marble drawn at random came from the first of three bags, each containing a mix of white and black marbles, given that we already know a white marble was drawn. Bayes' Theorem helps us find this probability.
This article delves into Bayes' Theorem, covering its statement, proof, derivation, and formula, as well as its various applications through different examples.
What is Bayes’ Theorem?
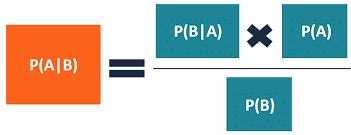
Bayes' Theorem, also known as Bayes' Rule or Bayes' Law, is a principle used to determine the conditional probability of event A given that event B has already occurred.
The theorem is expressed as follows:
P(A|B) = P(B|A)P(A) / P(B)
where:
- P(A) and P(B) are the probabilities of events A and B, respectively.
- P(A∣B) is the probability of event A occurring given that event B has occurred.
- P(B∣A) is the probability of event B occurring given that event A has occurred.
Statement of Bayes' Theorem
For a set of n events E1, E2,…, En within a sample space S, where each event Ei has a non-zero probability and these events partition the sample space, Bayes' Theorem states: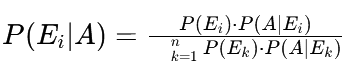
where A is the event for which we are calculating the probability given the set of events E1, E2,…,En.
Formula:
For any two events A and B, Bayes' Theorem can be formulated as:
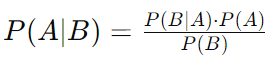
where:
- P(A) and P(B) are the probabilities of events A and B, respectively, with P(B)= 0.
- P(A∣B) is the probability of A given B.
- P(B∣A) is the probability of B given A.
Derivation of Bayes' Theorem
The proof of Bayes’ Theorem is given as, according to the conditional probability formula,
P(Ei|A) = P(Ei∩A) / P(A)…..(i)
Then, by using the multiplication rule of probability, we get
P(Ei∩A) = P(Ei)P(A|Ei)……(ii)
Now, by the total probability theorem,
P(A) = ∑ P(Ek)P(A|Ek)…..(iii)
Substituting the value of P(Ei∩A) and P(A) from eq (ii) and eq(iii) in eq(i) we get,
P(Ei|A) = P(Ei)P(A|Ei) / ∑ P(Ek)P(A|Ek)
Bayes' Theorem, often referred to as the formula for the probability of "causes," gives us the probability of a particular event Ei given that event A has occurred. This is based on the fact that the Ei's form a partition of the sample space S, meaning that one of these events must occur at any given time.
Key Terms Related to Bayes' Theorem
- Hypotheses: The events E1, E2,…,En in the sample space are referred to as hypotheses.
- Prior Probability: This is the initial probability of an event occurring before incorporating any new data. For hypothesis Ei, this is P(Ei).
- Posterior Probability: This represents the updated probability of an event after considering new information. For hypothesis Ei, it is P(Ei∣A).
- Conditional Probability: This is the probability of an event A given that another event B has occurred, denoted as P(A∣B).
- Joint Probability: This measures the probability of two or more events occurring together and is denoted as P(A∩B) for events A and B.
- Random Variables: These are real-valued variables whose possible values are determined by random experiments. The probability associated with these variables is called experimental probability.
Applications of Bayes' Theorem
Bayesian inference, which is derived from Bayes' Theorem, has numerous applications across various fields including medicine, science, philosophy, engineering, sports, and law. For example, in medicine, Bayes' Theorem helps evaluate the accuracy of medical tests by considering the likelihood of a disease and the overall accuracy of the test.
Difference Between Conditional Probability and Bayes' Theorem
To understand the difference between Conditional Probability and Bayes' Theorem, refer to the comparative table provided below.

Theorem of Total Probability
Let's consider a scenario where we have a set of mutually exclusive and exhaustive events E1, E2, ..., En associated with a random experiment, and let E be an event that occurs with at least one of these events. The theorem states that the probability of event E happening is given by:
P(E) = n∑i=1P(E/Ei) . P(Ej)
Proof:
Let S be the sample space. Then,
S = E1 ∪ E2 ∪ E3 ∪ . . . ∪ En and Ei ∩ Ej = ∅ for i ≠ j.
E = E ∩ S
⇒ E = E ∩ (E1 ∪ E2 ∪ E3 ∪ . . . ∪ En)
⇒ E = (E ∩ E1) ∪ (E ∩ E2) ∪ . . . ∪ (E ∩ En)
P(E) = P{(E ∩ E1) ∪ (E ∩ E2)∪ . . . ∪(E ∩ En)}
⇒ P(E) = P(E ∩ E1) + P(E ∩ E2) + . . . + P(E ∩ En)
{Therefore, (E ∩ E1), (E ∩ E2), . . . ,(E ∩ En)} are pairwise disjoint}
⇒ P(E) = P(E/E1) . P(E1) + P(E/E2) . P(E2) + . . . + P(E/En) . P(En) [by multiplication theorem]
⇒ P(E) = n∑i=1P(E/Ei) . P(Ei)
Conclusion
Bayes' Theorem is a powerful tool for updating probabilities based on new information. By combining prior knowledge with observed data, it enhances decision-making in fields like statistics, machine learning, medicine, and finance. Its applications range from medical diagnosis to spam filtering and beyond.
Understanding and applying Bayes' Theorem improves prediction accuracy, uncertainty estimation, and insights drawn from data, enabling better decision-making in complex and uncertain scenarios.
Bayes Theorem Examples
Example 1: A person has undertaken a job. The probabilities of completion of the job on time with and without rain are 0.44 and 0.95 respectively. If the probability that it will rain is 0.45, then determine the probability that the job will be completed on time.
Sol:
Let E1 be the event that the mining job will be completed on time and E2 be the event that it rains. We have,
P(A) = 0.45,
P(no rain) = P(B) = 1 − P(A) = 1 − 0.45 = 0.55
By multiplication law of probability,
P(E1) = 0.44, and P(E2) = 0.95
Since, events A and B form partitions of the sample space S, by total probability theorem, we have
P(E) = P(A) P(E1) + P(B) P(E2)
⇒ P(E) = 0.45 × 0.44 + 0.55 × 0.95
⇒ P(E) = 0.198 + 0.5225 = 0.7205
So, the probability that the job will be completed on time is 0.7205
Example 2: Suppose 15 men out of 300 men and 25 women out of 1000 are good orators. An orator is chosen at random. Find the probability that a male person is selected.
Sol:
Gievn,
- Total Men = 300
- Total Women = 1000
- Good Orators among Men = 15
- Good Orators among Women = 25
Total number of good orators = 15 (from men) + 25 (from women) = 40
Probability of selecting a male orator:
P(Male Orator) = Numbers of male orators / total no of orators = 15/40
|
145 videos|236 docs|166 tests
|
FAQs on Bayes Theorem - Crash Course for UGC NET Commerce
| 1. What is Bayes Theorem and how is it used in statistics and probability? |  |
| 2. How can Bayes Theorem be applied in the context of UGC NET exams? |  |
| 3. What are some common misconceptions about Bayes Theorem in the field of statistics and probability? |  |
| 4. How can students improve their understanding and application of Bayes Theorem for UGC NET preparation? |  |
| 5. Can Bayes Theorem be used to predict the outcome of UGC NET exams with 100% accuracy? |  |















