Number Play Chapter Notes | Mathematics (Maths) Class 6 PDF Download

Introduction

Numbers play a vital role in our daily lives, helping us organize and manage various tasks. We've used them for counting, as well as performing basic operations like addition, subtraction, multiplication, and division to solve everyday problems. 

Examples of Situations Where We Use Numbers:

1. Telling Time: We use numbers to read the time on a clock.
2. Shopping: Numbers are used to calculate the total cost of items and to manage money.
3. Cooking: Recipes often require specific measurements of ingredients, which involve numbers.
4. Traveling: Numbers help us understand distances, speed, and time during travel.
5. Sports: Scores, time limits, and player statistics all involve numbers.

Numbers Can Tell Us Things

Imagine a scenario where students are lined up for a school race. Each student announces a number, which represents something about their position in the line.
Let’s figure out what these numbers might mean:

• A student says ‘1’ if there is one faster runner next to them.
• A student says ‘2’ if both students next to them are faster.
• A student says ‘0’ if neither of the students next to them is faster.

In this case, each student is counting how many of their neighbors are faster runners.

Supercell

A supercell is a number in a grid that is larger than all of its neighboring numbers. The neighbors of a cell are the numbers directly to the left, right, above, and below it. Let’s say we have a grid of numbers, and our task is to find the supercells.
Example: Imagine a grid with the numbers 45, 78, 92, 31, and 60 arranged in a row.

92 would be a supercell if it's greater than 78 (to its left) and 31 (to its right).

Patterns of Numbers on the Number Line

Let’s practice placing some numbers on them. Imagine you have the following numbers: 2180, 2754, 1500, 3600, 9950, 9590, 1050, 3050, 5030, 5300, and 8400. These numbers need to be positioned correctly on the number line.
Here’s a basic number line to help you visualize: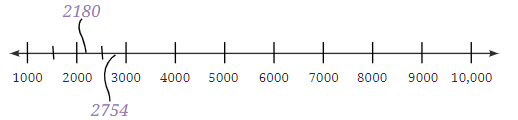

• 2180 would be placed slightly after 2000 but before 3000.
• 9950 would be very close to 10,000.
• 3050 would be just after 3000, and so on.

Playing with Digits

When we start counting numbers, we write them in order: 1, 2, 3, and so on. Let’s explore how many numbers exist with different digit lengths.

1. 1-digit numbers: These are the numbers from 1 to 9, so there are 9 one-digit numbers.
2. 2-digit numbers: These numbers range from 10 to 99. To find out how many there are:
   • Subtract the smallest two-digit number (10) from the largest (99) and add 1.
   • 99 - 10 + 1 = 90
   • So, there are 90 two-digit numbers.
3. 3-digit numbers: These numbers range from 100 to 999.
   • 999 - 100 + 1 = 900
   • So, there are 900 three-digit numbers.
4. 4-digit numbers: These numbers range from 1000 to 9999.
   • 9999 - 1000 + 1 = 9000
   • So, there are 9000 four-digit numbers.
5. 5-digit numbers: These numbers range from 10,000 to 99,999.
   • 99,999 - 10,000 + 1 = 90,000
   • So, there are 90,000 five-digit numbers.

Digit Sums of Numbers

Rajat noticed an interesting pattern: sometimes, when you add the digits of different numbers, the sums are the same.
For example: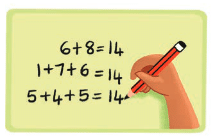

• 68: 6 + 8 = 14
• 176: 1 + 7 + 6 = 14
• 545: 5 + 4 + 5 = 14

All of these numbers have a digit sum of 14!

Digit Detectives

Mahi had a curious thought: how often does the digit ‘7’ appear when writing all the numbers from 1 to 100 or even 1 to 1000?

• 1 to 100: The digit ‘7’ appears in the 7th, 17th, 27th, 37th, 47th, 57th, 67th, 70-79 (10 times), and 87th, 97th. This totals to 20 times.

• 1 to 1000: The digit ‘7’ will appear more frequently in three positions (hundreds, tens, and units) across all numbers from 1 to 1000. Calculating this for each position involves counting how often ‘7’ appears in each digit place:
• Units place: 100 times (7, 17, 27...997)
• Tens place: 100 times (70-79 in each hundred)
• Hundreds place: 100 times (700-799)
• So, the digit ‘7’ appears 300 times between 1 and 1000.

Pretty Palindromic Patterns

Palindromic numbers are numbers that read the same forward and backward. For example, numbers like 66, 848, 575, 797, and 1111 are all palindromes because they look the same whether you read them from left to right or right to left.

Creating 3-Digit Palindromes

Let’s explore how to create all possible 3-digit palindromes using the digits 1, 2, and 3. A 3-digit palindrome has the same first and third digits. Here’s how they look:

1. 121: The first and last digits are 1, and the middle digit is 2.
2. 131: The first and last digits are 1, and the middle digit is 3.
3. 212: The first and last digits are 2, and the middle digit is 1.
4. 232: The first and last digits are 2, and the middle digit is 3.
5. 313: The first and last digits are 3, and the middle digit is 1.
6. 323: The first and last digits are 3, and the middle digit is 2.

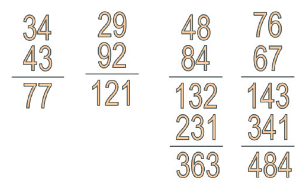
These are all the possible 3-digit palindromes you can create using only the digits 1, 2, and 3.

Reverse-and-Add Palindromes

Now, let’s explore a fun activity involving palindromes, called the Reverse-and-Add method. Here’s how it works:

1. Start with a 2-digit number. For example, let’s pick 34.
2. Reverse the digits of the number: 34 becomes 43.
3. Add the original number to its reverse:
   • 34 + 43 = 77
4. Check if the result is a palindrome. If it is, you’re done. If not, reverse the new number and add again.

Let’s try another example with a different number, 47:

• Reverse 47 to get 74.
• Add them: 47 + 74 = 121.
• Since 121 is a palindrome, we stop here.

Let’s try with 89:

• Reverse 89 to get 98.
• Add them: 89 + 98 = 187 (not a palindrome, so continue).
• Reverse 187 to get 781.
• Add them: 187 + 781 = 968 (not a palindrome, so continue).
• Reverse 968 to get 869.
• Add them: 968 + 869 = 1837 (still not a palindrome).

In this case, you would keep repeating the process until you get a palindrome. Some numbers take several steps to become a palindrome, while others might never reach one!

Puzzle Time

Here’s a fun puzzle to solve:

• I am a 5-digit palindrome.
• I am an odd number.
• My ‘t’ digit (third digit) is double of my ‘u’ digit (second digit).
• My ‘h’ digit (fourth digit) is double of my ‘t’ digit.

Let’s break it down:

1. Since it’s a 5-digit palindrome, the first and fifth digits are the same, and the second and fourth digits are the same.
2. The middle digit (third) stands alone and must be odd because the number is odd.
3. Let’s assume the second digit (u) is 2; then the third digit (t) would be 4, and the fourth digit (h) would be 8.

But let’s think carefully:

• If the second digit is 1, the third digit should be 2, and the fourth digit should be 4. This works well because the number must remain a palindrome.
• Hence, the number is 14641.

The Magic Number of Kaprekar

D.R. Kaprekar was a mathematics teacher from Devlali, Maharashtra, who had a deep love for numbers. He discovered many interesting patterns in numbers that had never been seen before. One of his most famous discoveries is the Kaprekar constant, a magical number associated with 4-digit numbers. 

Steps to Discover the Magic:

1. Pick any 4-digit number (e.g., 6382).
2. Arrange the digits to form the largest possible number. Call this A.
   • For 6382, the largest number is 8632.
3. Rearrange the digits to form the smallest possible number. Call this B.
   • For 6382, the smallest number is 2368.
4. Subtract B from A to get a new number, C.
   • Subtract: 8632 - 2368 = 6264.

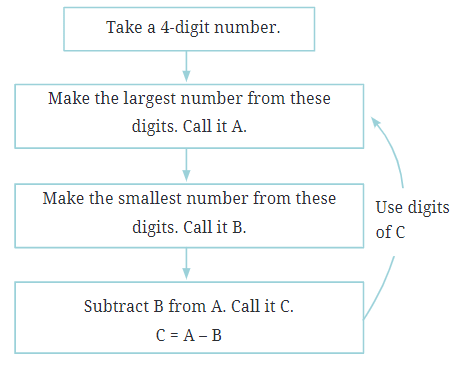
What Happens Next?

Take the number C and repeat the process:
Start with 6264:

• Largest number (A): 6642
• Smallest number (B): 2466
• Subtract: 6642 - 2466 = 4176

Continue with 4176:

• Largest number (A): 7641
• Smallest number (B): 1467
• Subtract: 7641 - 1467 = 6174

No matter what 4-digit number you start with, if you repeat these steps, you will always eventually reach the number 6174. This number is called the Kaprekar constant.

What About 3-Digit Numbers?

If you carry out the same steps with 3-digit numbers, you will find that the number 495 starts repeating. This is the Kaprekar constant for 3-digit numbers.

Clock and Calendar Numbers

Clocks and calendars aren't just tools to tell time or date; they also have interesting patterns hidden in their numbers.

Clock Patterns

A 12-hour clock presents interesting opportunities to find patterns in time.
For example:

• 4:44: This is a time where all the digits are identical.
• 10:10: Here, the digits repeat in a mirrored fashion.
• 12:21: This time is palindromic, meaning it reads the same forward and backward.

Finding Other Patterns

• 1:11: Similar to 4:44, all digits are the same.
• 2:22: Another example of identical digits.
• 3:33: Continuing the pattern of repeating digits.
• 5:55: Following the same format.
• 11:11: A widely recognized time, often noted for its symmetry.

Beyond these straightforward examples, you can also find other interesting patterns like:

• 12:12: A time where the hour and minute digits repeat the same number.
• 2:20: The hour digit and the first digit of the minutes match.
• 5:05: The hour digit and the last digit of the minutes are the same.

These patterns can be fun to spot and show how even something as routine as checking the time can reveal hidden numerical beauty.

Calendar Patterns

Certain dates stand out because of how their digits repeat or follow a particular sequence. For example, 20/12/2012 is interesting because the digits 2, 0, 1, and 2 repeat.
This kind of pattern can be found in other dates as well:

• 02/10/2001: Here, the digits 2, 0, 1 repeat, but in a different order.
• 12/02/2001: A similar repeating pattern is seen.
• 10/02/2010: The digits 1, 0, 2, and 0 appear.

These dates catch our attention because of their symmetry or repetition, making them memorable.

Palindromic Dates Like 11/02/2011

Palindromic dates are particularly special because they read the same forwards and backwards.
Examples include:

• 02/02/2020: This date is fully palindromic.
• 11/11/2011: A date where all digits are identical and the entire date is a palindrome.
• 21/02/2012: Another palindromic date with a different sequence.

These dates are rare and often seen as special or lucky due to their symmetrical nature.

Reusing Calendars

Jeevan’s curiosity about reusing calendars is a great question. The truth is, while we typically need a new calendar each year, certain years can share the exact same calendar. This is because the calendar repeats when the days of the week fall on the same dates, which depends on several factors including whether it’s a leap year.

A leap year happens every 4 years to keep our calendar in sync with the Earth's orbit around the Sun. For example, the year 2024 is a leap year, so February will have 29 days instead of 28.

Mental Math

The numbers in the middle column are combined to create the numbers on the sides. You can use the numbers in the middle multiple times if needed.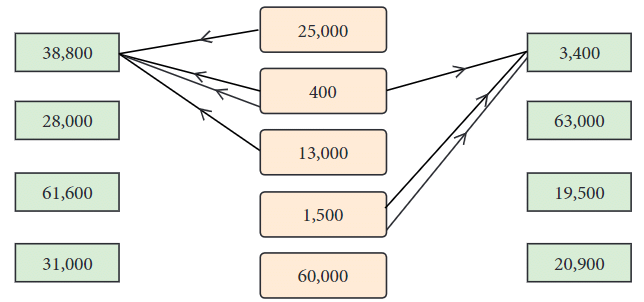

Examples: 38,800

• Calculation: 25,000 + 400 × 2 + 13,000.
• Breakdown: Start with 25,000, add 800 (400 twice), then add 13,000.

Adding and Subtracting

Example: 39,800

• Calculation: 40,000 – 800 + 300 + 300.
  
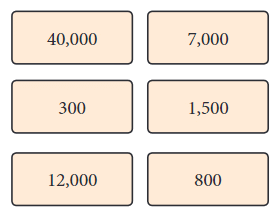
• Breakdown: Start with 40,000, subtract 800, then add 300 twice.

Digits and Operations

Here are two examples:

• Adding Two 5-Digit Numbers: 12,350 + 24,545 = 36,895
• Subtracting Two 5-Digit Numbers: 48,952 - 24,547 = 24,405

Playing with Number Patterns

When given a set of numbers arranged in patterns, there are often quicker ways to sum them rather than adding each number individually. Recognizing patterns can help simplify and speed up calculations.

From the Book

In these images, we have numbers arranged in different patterns. The task is to find the sum of the numbers in each pattern. Instead of adding them one by one, we can use some tricks to find the sum faster.
Pattern a: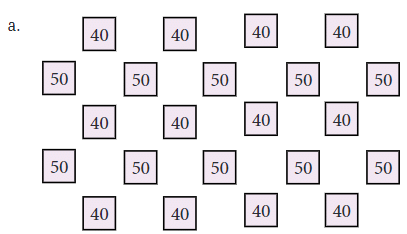

• Numbers Involved: 40 and 50
• Quick Calculation: Notice that 50 is in the center surrounded by 40s. Add the numbers by grouping them or using multiplication to speed up the calculation.
• Solution: Numbers Involved: 40 and 50

  Step 1: Counting the numbers
  We have 6 "50s" and 19 "40s" in the pattern.
  Step 2: Multiply the numbers
  Multiply the number of 50s by 50:
  6 × 50 = 300
  Multiply the number of 40s by 40:
  19 × 40 = 760
  Step 3: Add them together
  300 + 760 = 1060
  Final Answer:The total sum for the numbers in this pattern is 1060.

Pattern b: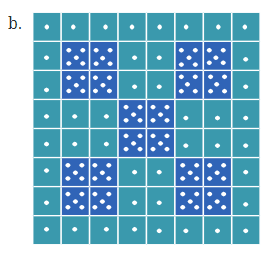

• Pttern Involved: Small squares filled with dots
• Quick Calculation: Count the number of squares and multiply by the number of dots in each square. This gives the total number of dots quickly.
• Solution: Step 1: Count the squares
  There are 49 squares in total.
  Step 2: Identify the types of squares
  36 squares have 1 dot each.
  13 squares have 9 dots each.
  Step 3: Multiply and sum the dots
  Dots in squares with 1 dot:
  36 × 1 = 36
  Dots in squares with 9 dots:
  13 × 9 = 117
  Step 4: Add them together
  36 + 117 = 153
  Final Answer: The total number of dots in the pattern is 153.

Pattern c: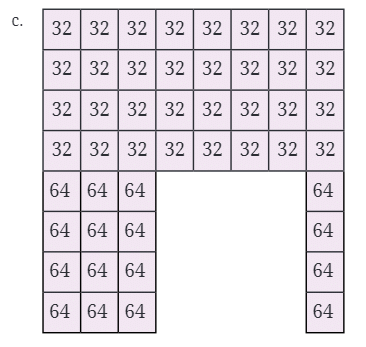

• Numbers Involved: 32 and 64
• Quick Calculation: The pattern is mostly made of 32, but the bottom part has 64s. You can multiply the number of 32s and 64s separately and then add them together to get the total.
• Solution:Numbers Involved: 32 and 64
  

  Step 1: Counting the numbers
  We have 28 "32s" and 9 "64s" in the pattern.
  Step 2: Multiply the numbers
  Multiply the number of 32s by 32:
  28 × 32 = 896
  Multiply the number of 64s by 64:
  9 × 64 = 576
  Step 3: Add them together896 + 576 = 1472
  Final Answer: The total sum for the numbers in this pattern is 1472.

Pattern d: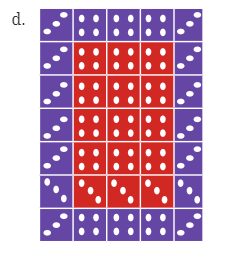

• Numbers Involved: More squares with dots
• Quick Calculation: Similar to Pattern b, count the squares with dots and multiply. Pay attention to the different colors, as they might represent different groups.
• Solution:

• Step 1: Identify the squares

  Purple squares have 4 dots each.

  Red squares have 6 dots each.

  Step 2: Count the number of squares

  Purple squares: 20 squares with 4 dots.

  Red squares: 9 squares with 6 dots.

  Step 3: Multiply the dots

  Dots in purple squares: 20 × 4 = 80

  Dots in red squares: 9 × 6 = 54

  Step 4: Add them together

  80 + 54 = 134

  Final Answer: The total number of dots in the pattern is 134.

Pattern e:

• Numbers Involved: 15, 25, and 35
• Quick Calculation: This pattern is circular. Group the same numbers and multiply by the number of times they appear.
• Solution:  Step 1: Identify the numbers involvedNumbers involved: 15, 25, and 35.
  Step 2: Count the number of times each number appears
  15 appears 15 times.
  25 appears 16 times.
  35 appears 13 times.
  Step 3: Multiply the numbers by the number of times they appear
  15 × 15 = 225
  25 × 16 = 400
  35 × 13 = 455
  Step 4: Add the results
  225 + 400 + 455 = 1080
  Final Answer: The total sum for Pattern e is 1080.

Pattern f: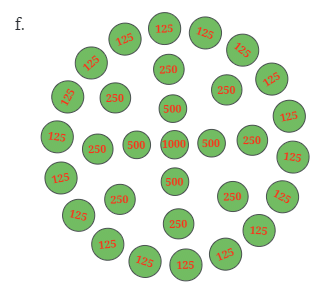

• Numbers Involved: 125, 250, 500, 1000
• Quick Calculation: The numbers increase as you move towards the center. Calculate the sum by adding the outer circles first and then move inward.
• Solution: Step 1: Identify the numbers involvedNumbers involved: 125, 250, 500, and 1000.
  Step 2: Count the number of times each number appears
  125 appears 12 times.
  250 appears 9 times.
  500 appears 6 times.
  1000 appears 1 time.
  Step 3: Multiply the numbers by the number of times they appear
  125 × 12 = 1500
  250 × 9 = 2250
  500 × 6 = 3000
  1000 × 1 = 1000
  Step 4: Add the results
  1500 + 2250 + 3000 + 1000 = 7750
  Final Answer: The total sum for Pattern f is 7750

An Unsolved Mystery - the Collatz Conjecture

The Collatz Conjecture is an intriguing mathematical sequence that remains unsolved. Here's how the sequences work:

Sequences Examples:

• Sequence a: 12, 6, 3, 10, 5, 16, 8, 4, 2, 1
• Sequence b: 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
• Sequence c: 21, 64, 32, 16, 8, 4, 2, 1
• Sequence d: 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1

Rule Applied:

• Even Number: Divide by 2.
• Odd Number: Multiply by 3 and add 1.
• Repeat: Continue applying the rule to the result.

Each sequence, no matter what number you start with, eventually reaches 1. This observation is central to the Collatz Conjecture.

Simple Estimation

Estimation helps when you don't need the exact number and just want a quick idea. For example, if you’re estimating how many books are in the library, you might guess based on what you see rather than counting each one.

Example 1: Estimating the Number of Books in a Library

• You know there are about 300 books on each shelf.
• There are 10 shelves in the library.
• Estimate: Instead of counting every book, you multiply 300 by 10 and estimate there are around 3,000 books in the library.

Example 2: Estimating Guests at a Party

• You see that each table at a party has about 8 people.
• There are 12 tables.
• Estimate: Multiply 8 by 12 to estimate that there are about 100 people at the party.

Games and Winning Strategies

Numbers can be used in fun games where you need to think ahead and plan to win.

Game #1: The Game of 15

Rules:

• Players take turns picking a number between 1 and 5.
• The number they pick is added to a running total.
• The first player to make the total reach 15 wins.

Winning Strategy:

• To always win, try to leave the total at 10 after your turn.
• For example, if your opponent picks numbers that make the total 9, you should pick 1 to bring it to 10. This way, you can control the game and eventually reach 15.

Game #2: The Game of 50

Rules:

• The first player picks a number between 1 and 7.
• Players take turns adding a number between 1 and 7 to the running total.
• The first player to make the total reach 50 wins.

Winning Strategy:

• Aim to make the running total hit key numbers like 43, 36, 29, or 22.
• If your opponent leaves the total at 42, you should add 1 to make it 43. This gives you an advantage to win the game.

Creating Your Own Game Variations

• Example Variation:
  • Change the winning number to 30 and allow adding numbers between 1 and 4.
  • Figure out which numbers you should aim for to always have the best chance of winning.

These games help you practice thinking ahead, which is a great skill not just for games but for solving problems in general. By learning the patterns and strategies, you can become the player who always wins!